Виды деформации в области кончика трещины

Модель тела с трещинами

Общим для различных моделей развития трещины в твердых телах является заданное в начальный момент некоторое распределение тре­щины конечной длины.

До 40-х гг. XX в. было распространено мнение, что разрушение происходит почти мгновенно. В последующие десятилетия установили, что развитие трещины занимает значительный период, предшествующий разрушению.При изменении внешних нагрузок трещины развиваются устойчиво, не приводя к разрушению конструкцию, спроектированную с учетом имеющихся начальных трещин.

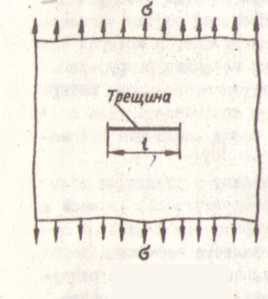
В 1920 г. А. Гриффитс, используя энергетический подход, полу­чил условие разрушения бесконечной пластинки (риз. I) с щелевой трещиной длиной t:

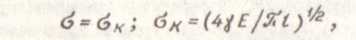(1)

 

Где Ϭ_к - критическое напряжение, соответствующее возникновению неустойчивости трещиш; γ - поверхностная энергия материала;

Е ~ модуль упругости.

Условие (I) определяет катастрофическое распространение трещи­ны и справедливо для хрупких материалов типа стекла или керамики.

Пусть в теле имеется трещина неко­торой длины t. Тогда с увеличением напряжения Ϭ трещина не будет разви­ваться до тех пор, пока напряжение не достигнет значения Ϭ_к, критическо­го для данной трещины. Как только это значение будет достигнуто, произойдет неустойчивое, спонтанное развитие тре­щины и тело разрушится.

Рис.1

Теория А. Гриффитса не позволяла учесть некоторые важные аспекты процес­са разрушения. Е. Орован и Дж. Ирвин обнаружили,что хрупкое разрушение вы­сокопрочных материалов сопровождается существенными пластическими деформациями в тонком слое вблизи по­верхности трещины. Такое разрушение было названо квазихрупким.

Дж. Ирвин и Е. Орован выдвинули свою концепцию квазихрупкого раз­рушения, основная идея которой заключается в учете энергии, необ­ходимой для пластической деформации. Это позволило расширить пре­делы применимости теории А. Гриффитса.

Хрупким и квазихрупким разрушением не охватывается разнообра­зие видов разрушения. Возможны также упругопластическое, вязкое, вязкоупругое и другие виды разрушения.

Важнейшим моментом при изучении любого из этих видов разруше­ния является формулировка условия разрушения в кончике трещины. Наиболее просто это условие формулируется в теории квазихрупкихх трещин, когда пластическая деформация считается сосредоточенной в тонком слое вблизи поверхности трещины. Простейший вариант этого условия был предложен Дж. Ирвином, который в конце 50-х гг. наше­го века, изучив оптическими методами напряженное состояние вокруг кончика трещины, обосновал понятие коэффициента интенсивности на­пряжений. Исследование Дж. Ирвина открыло путь для анализа упру­гих напряжений в телах с трещинами.

 

Виды деформации в области кончика трещины

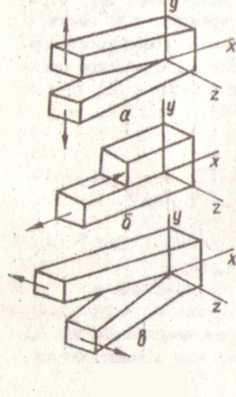
Трещины хрупкого разрушения в твердых телах можно рассматри­вать как поверхности разрыва вектора смещений. Существует три ви­да независимых кинематических движений верхней и нижней поверхно­стей трещины по отношению друг к другу. На рис.2 изображены ло­кальные смещения элемента, содержащего фронт трещины.

Указанные три типа деформаций являются необходимыми и достаточными для описания всех возможных видов поведения трещины в наиболее общем случае расцределения упругих напряжений. Типы движений для трещины, лежащей в плоскости X Z, можно описать следующим образом.

Нормальный отрыв (рис. 2,а) характе­ризуется такими перемещениями поверхнос­тей трещины, при которых последние стре­мятся разойтись симметрично относительно плоскости, в которой была расположена трещина до деформации.

Поперечный сдвиг (рис. 2,6) представляет собой локальную деформацию, при ко­торой поверхности трещины скользят одна по другой в одной плоскости, но в проти­воположных направлениях.

Рис.2

 

При продольном сдвиге (рис. 2,в) поверхности трещины скользят одна по другой в направлении, параллельном линии фронта трещины.

Естественно, что каждое из трех движений поверхностей трещины, изображенных на рис. 2, связано с соответствующим полем напряже­ний в окрестности кончика трещины.