Объектом статистического изучения в социальных науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных уравнений регрессии недостаточно для описания таких систем и объяснения механизмов их функционирования. При использовании отдельных уравнений регрессии, например для экономических расчетов, в большинстве случаев предполагается, что аргументы (факторы) можно изменять независимо друг от друга. Однако это предположение является очень грубым: практически изменение одной переменной повлечет за собой изменения во всей системе взаимосвязанных признаков. Этим объясняется необходимость использования не отдельных уравнений, а их систем.
Система уравнений в эконометрических исследованиях может быть построена по-разному.
Возможна система независимых уравнений, когда каждая зависимая переменная рассматривается как функция одного и того же набора факторов:
Примером такой модели может служить модель экономической эффективности сельскохозяйственного производства, где в качестве зависимых переменных выступают показатели эффективности производства (производительность, себестоимость продукции и т.д.), а в качестве факторов – характеристики самого хозяйства (количество голов скота, площадь пашни и т.д.).
Для системы независимых уравнений каждое уравнение может рассматриваться самостоятельно, и его параметры определяются обычным образом по методу наименьших квадратов.
Наибольшее распространение в эконометрических исследованиях получила система взаимосвязанных уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть системы, а в других – в правую часть:
Система взаимосвязанных уравнений получила название системы совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. Каждое уравнение такой системы не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются его модификации: косвенный, двухшаговый и трехшаговый метод наименьших квадратов.
Примером системы одновременных уравнений может служить модель динамики цены и заработной платы вида
где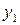 
- темп изменения месячной заработной платы;
- темп изменения цен;
- процент безработных;
- темп изменения постоянного капитала;
- темп изменения цен на импорт сырья.
