До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель факторы, которые представляют собой различные атрибутивные признаки. Такими признаками, например, являются профессия, пол, образование, климатические условия и т.п. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные преобразовать в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.
Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид:
,
где y – количество потребляемого кофе;
x – цена кофе.
Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: 
и женского пола: 
. Если сила влияния цены на количество потребления кофе одинакова как для мужчин, так и для женщин (
), то становится возможным построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Это уравнение может быть записано в виде:
,
где 
- фиктивные переменные, принимающие значения:
.
Следует отметить, что применение МНК для оценивания параметров 
и 
приводит к вырожденной матрице исходных данных, а следовательно, и к невозможности получения их оценок.
Выходом из создавшегося положения может явиться переход к уравнению
,
т.е. уравнению, включающему только одну фиктивную переменную. Предположим, что МНК были получены оценки параметров этого уравнения, тогда теоретические значения размера потребления кофе для мужчин будут получены из уравнения
.
Для женщин соответствующие значения получим из уравнения
.
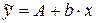Модели временных рядов
Обычно эконометрические модели строятся на основе двух типов исходных данных:
· данные, характеризующие совокупность различных объектов в определенный момент (период) времени;
· данные, характеризующие один объект за ряд последовательных моментов (периодов) времени.
Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов.
Временной ряд – совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:
· факторы, формирующие тенденцию ряда (например, инфляция влияет на увеличение размера средней заработной платы);
· факторы, формирующие циклические колебания ряда (например, уровень безработицы в курортных городах в зимний период выше по сравнению с летним);
· случайные факторы.
Очевидно, что реальные данные чаще всего содержат все три компоненты. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Если же временной ряд представлен как их произведение, то такая модель называется мультипликативной.
При наличии в временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют уровнями автокорреляцией уровней ряда. Количественно эту зависимость с помощью коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутого на несколько шагов во времени.
Пример. Пусть имеются условные данные о средних расходах на конечное потребление (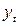
, денежных единиц) за 8 лет.
| t |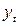
| 
| 
| 
| 
| 
| 
|
| - | - | - | - | - | - | ||
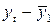
| -3,39 | -3 | 9,87 | 10,8241 | ||||
| -3,29 | -2 | 6,58 | 10,8241 | ||||
| -1,29 | -2 | 2,58 | 1,6641 | ||||
| -0,29 | 0,00 | 0,0841 | |||||
| 0,71 | 0,71 | 0,5041 | |||||
| 2,71 | 5,42 | 7,3441 | |||||
| 4,71 | 18,84 | 22,1841 | |||||
| S | -0,03 | 44,0 | 53,4287 |
По формулам
вычисляем
,
.
Далее, заполняем таблицу и используя формулу для вычисления линейного коэффициента корреляции, получаем
.
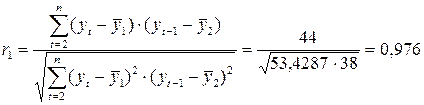Полученное значение свидетельствует об очень тесной зависимостью между расходами на конечное потребление текущего непосредственно предшествующего годов и, следовательно, о наличии во временном ряде расходов на конечное потребление сильной линейной тенденции.
Нами был посчитан коэффициент автокорреляции для смещения на один год. Такой коэффициент называется коэффициентом первого порядка. При смещении на два года получим коэффициент второго порядка и так далее. Число периодов (в данном случае лет), по которым рассчитывается коэффициент автокорреляции, называется лагом.
Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени. Поскольку зависимость может принимать различные формы, то ее формализации можно использовать различные виды функций: линейную, гиперболическую, параболическую, степенную и т.п. Параметры каждой из перечисленных моделей могут быть найдены по МНК.
