На этапе идентификации полученных моделей парной регрессии рассчитываются показатели тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции (rxy):
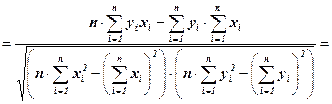
Корреляционная связь между переменными называется прямой, если rxy > 0, и обратной, если rxy < 0.
Коэффициент корреляции принимает значения от -1 до 1, т. е. -1 £ rxy £ 1. Чем ближе коэффициент корреляции rxy к единице, тем связь теснее. Для качественной характеристики силы связи используют шкалу Чеддока:
| Показатель тесноты связи | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 |
| Характеристика силы связи | слабая | умеренная | заметная | высокая | весьма высокая |
Связь между переменными х и у модели тесная (высокая), прямо пропорциональная.
| x | y | yx | (y -` y)2 | (yx- ` y)2 | (y - yx)2 | (x -` x)2 | x 2 |
| 201,6 | 1011,3 | 1049,6 | 408537,6 | 1463,342 | 40642,56 | ||
| 242,6 | 1490,4 | 1101,5 | 39332,04 | 344788,1 | 151214,8 | 214486,5 | 58854,76 |
| 255,4 | 1024,5 | 1117,8 | 441192,3 | 325992,8 | 8698,412 | 202794,3 | 65229,16 |
| 323,7 | 559,9 | 1204,4 | 234606,6 | 415330,1 | 145944,6 | 104781,7 | |
| 331,9 | 1195,1 | 1214,8 | 243663,7 | 224643,2 | 386,4227 | 139746,6 | 110157,6 |
| 384,6 | 1050,1 | 1281,6 | 407839,4 | 165769,9 | 53580,49 | 103122,5 | 147917,2 |
| 397,7 | 1482,8 | 1298,2 | 42404,31 | 34083,16 | 94880,59 | 158165,3 | |
| 450,7 | 1151,7 | 1365,4 | 288393,8 | 104550,1 | 45659,6 | 65038,73 | 203130,5 |
| 457,6 | 1020,6 | 1374,1 | 446388,4 | 98969,18 | 61566,97 | 209397,8 | |
| 515,3 | 1447,3 | 1658,369 | 58291,99 | 40286,22 | 36262,41 | 265534,1 | |
| 533,8 | 2441,9 | 1470,7 | 567275,5 | 47516,01 | 29558,87 | 284942,4 | |
| 587,8 | 1424,6 | 1539,2 | 22355,18 | 13134,67 | 13906,76 | 345508,8 | |
| 614,9 | 1095,4 | 1573,6 | 352032,3 | 13261,16 | 228642,7 | 8249,53 | |
| 655,1 | 1278,5 | 1624,5 | 4120,171 | 119739,9 | 2563,085 | ||
| 720,1 | 2091,4 | 1706,9 | 162148,7 | 332,0869 | 147804,6 | 206,5853 | |
| 741,5 | 2403,5 | 1734,1 | 2057,144 | 448124,7 | 1279,713 | 549822,3 | |
| 760,9 | 1758,7 | 103218,9 | 4893,354 | 63163,96 | 3044,068 | 578968,8 | |
| 814,1 | 2042,3 | 1826,1 | 125016,6 | 18879,7 | 46730,99 | 11744,72 | 662758,8 |
| 859,2 | 1607,9 | 1883,3 | 6532,37 | 37863,14 | 75849,35 | 23553,99 | 738224,6 |
| 1683,2 | 1974,3 | 30,50438 | 81577,57 | 84763,06 | 50747,96 | ||
| 953,8 | 2003,3 | 25511,46 | 98926,23 | 224911,6 | 61540,25 | 909734,4 | |
| 1092,6 | 3063,9 | 2179,2 | 240596,4 | 782642,1 | 149670,8 | ||
| 1148,9 | 2048,4 | 2250,6 | 129367,5 | 315717,7 | 40889,17 | 196402,4 | |
| 1247,5 | 2034,4 | 2375,6 | 119492,5 | 471831,6 | 116433,2 | 293518,1 | |
| 1253,1 | 2435,9 | 2382,7 | 558273,4 | 481636,1 | 2827,775 | 299617,3 | |
| 1873,5 | 3082,1 | 3169,3 | 7605,97 | ||||
| Сумма |
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции r2xy, который называется коэффициентом детерминации. Он характеризует долю результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:
.
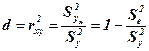Величина 1 – r 2 характеризует долю дисперсия у, вызванную влиянием остальных не учтённых в модели факторов.
Для получения несмещённой оценки общей дисперсии на одну степень свободы, общую сумму квадратов отклонений делят не на число единиц совокупности, а на число степеней свободы
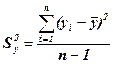= 10374477 / (26 – 1) = 414979,1,
факторная дисперсия
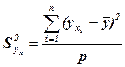= 6152378 / 1 = 6152378,
остаточная дисперсия
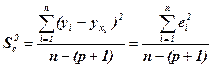= 4222098 / (26 – 2) = 175920,8,
дисперсия факторной переменной
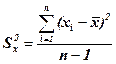= 3827285 / (26 – 1) = 153091,4,
где n – число наблюдений, р – число оцениваемых параметров уравнения при независимых переменных, (р + 1) – число оцениваемых параметров уравнения регрессии, включая константу b 0, yi – наблюдаемые значения зависимой переменной (i = 1, …, n),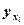 
или 
- расчётные значения зависимой переменной, xi – наблюдаемые значения независимой переменной.
Среднеквадратические отклонения:
общее Sy = 644,1887, факторное Syx = 2480,399, остаточное Se = = 419,4291, независимой переменной Sx = 391,269.
Вычисляя отношение факторной и остаточной дисперсии в расчете на одну степень свободы, получают величину F -критерия Фишера. Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н 0 необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз, т.е. выполнялась бы гипотеза 
.
Значение F -критерия Фишера для парной линейной регрессии:
34,95.
Вычисленное значение F -критерия признается достоверным (отличающимся от единицы), если оно больше табличного. Табличное значение F -критерия это максимальная величина отношения дисперсий, которая имеет место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. В этом случае нулевая гипотеза (Н 0) отвергается и делается вывод о существенности изучаемой связи: Fфакт > Fтабл.
Если величина Fфакт оказывается меньше Fтабл, то вероятность нулевой гипотезы выше заданного уровня (a = 0,05 или 0,01) и она не может быть отклонена без риска неверного вывода о наличии связи. В этом случае уравнение регрессии признается статистически незначимым.
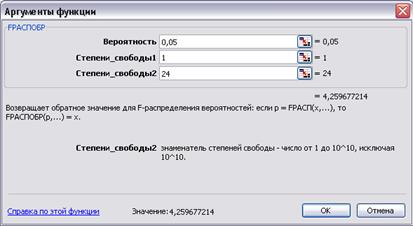
Полученное значение Fфакт = 34,95 сравниваем с табличным критическим значением, которое при уровне значимости a = 0,05 и числе степеней свободы k 1 = р = 1 (регрессионном) и k2 = n – р – 1 = = 26 – 1 – 1 = 24 (остаточном) составит Fтабл = = 4,259677. Так как Fфакт > Fтабл, то делаем вывод о существенности изучаемой связи по линейной модели, т.е. о статистической значимости модели в целом.
Критическое (табличное) значение F -критерия Фишера можно определить с помощью функции Excel FРАСПОБР из категории Статистические.
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров.
Процедура оценивания существенности параметров b 0 и b 1 базируется на расчете фактических значений t -критерия Стьюдента:
4,435949
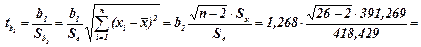= 5,838067,
которые затем сравниваются с табличным (критическим) значением для заданного уровня значимости a = 0,05 и числа степеней свободы (n – р –1) = (n– 2). Если фактическое значение t -критерия Стьюдента (по модулю) превышает табличное (t крит), то гипотезу о несущественности коэффициента регрессии можно отклонить.
Критическое (табличное) значение t -критерия Стьюдента можно определить с помощью функции Excel СТЬЮДРАСПОБР из категории Статистические.
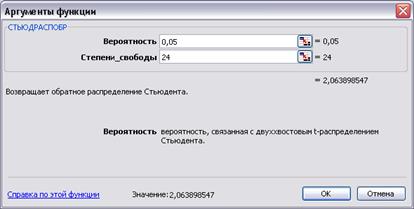
Поскольку ta; n-m-1 = t 0,05; 24 = tкр = tтабл = 2,063899, то в обоих случаях | tфакт | > tтабл, делаем вывод, что значения параметров b0 и b1 не случайно отклоняются от нуля, т.е. статистически значимы и отражают реальную природу взаимосвязей между рассматриваемыми переменными в рамках разработанной модели парной линейной регрессии.
Значимость коэффициента корреляции проверяется также на основе расчета фактического значения t -критерия Стьюдента:
5,9.
В парной линейной регрессии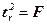 
, следовательно, оба способа проверки значимости модели (с помощью t и F -критерия) для линейной парной регрессии равносильны. Кроме того, 
.
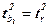Для проверки нулевой гипотезы Н 0 необходимо сравнить фактическое значение tr (по модулю) с табличным значением (при заданном уровне значимости a), если | tr | > t крит, то коэффициент корреляции значимо отличается от нуля.
Оценить качество синтезированной модели в целом можно основываясь на минимальности отклонения фактических значений результативного признака от теоретических, рассчитанных по уравнению регрессии. Величина отклонений эмпирических и расчетных значений (у–уx) по каждому наблюдению представляет собой абсолютную ошибку аппроксимации. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации, как среднюю арифметическую простую из относительных ошибок аппроксимации:
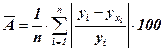= 21,9 %.
Полученное значение ошибки может быть использовано для сравнения моделей различных форм зависимостей.
При подстановке в уравнение регрессии у = b 0 + b 1 х соответствующего значения х можно определить предсказываемое (прогнозируемое) значение ур, как вариант точечного прогноза. Примем хp равным медиане (среднему значению из двух чисел, стоящих в центре ранжированного ряда величины х) хp = 635. Тогда
ур = 793,95 + 1,27 * 635 = 1599,05.
Поскольку точечный прогноз является усреднённой оценкой, то вероятные значения прогнозируемой величины будут находиться в некотором интервале. Поэтому точечный прогноз необходимо дополнить расчетом стандартной ошибки Syx и соответственно оценкой доверительного интервала теоретических значений результативного признака у:
.
Средняя стандартная ошибка расчетного значения результативного признака по уравнению регрессии:
;
где 
- остаточная дисперсия результативного признака в расчете на одну степень свободы,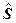 
- остаточное среднеквадратическое отклонение результативного признака.
; 
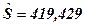млн.руб.
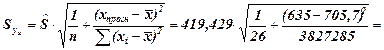83,64
С надёжностью a = 0,05 (табличное значение tk = 2,0639) доверительный интервал для yp при заданном хр = 635 составит
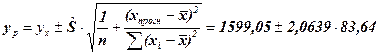
yp(min) = 1426,42 yp(max) = 1771,68 млн. руб.
Средняя ошибка предсказанного индивидуального значения у при хр = хk составит:
.
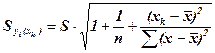Средняя ошибка прогнозируемого индивидуального значения у
427,7
Тогда при заданном уровне значимости доверительный интервал для ур при хр = хk составит:
,
где tk - критическое (табличное) значение t -критерия Стьюдента для соответствующего уровня значимости и числа степеней свободы (n - 2), tkS – предельная ошибка прогнозируемой величины.
Доверительный интервал для индивидуальных значений результативного признака
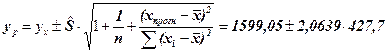
yp(min) = 716,346 yp(max) =2481,755
| x | y | yx | yp(min) | yp(max) | yp(min) | yp(max) |
| 201,6 | 1011,3 | 1049,554 | 769,2288 | 1329,879 | 139,6373 | 1959,47 |
| 242,6 | 1490,4 | 1101,536 | 835,4213 | 1367,652 | 195,897 | 2007,176 |
| 255,4 | 1024,5 | 1117,765 | 855,9867 | 1379,544 | 213,3905 | 2022,14 |
| 323,7 | 559,9 | 1204,361 | 964,7842 | 1443,938 | 306,1613 | 2102,561 |
| 331,9 | 1195,1 | 1214,758 | 977,727 | 1451,788 | 317,2337 | 2112,282 |
| 384,6 | 1050,1 | 1281,575 | 1060,186 | 1502,963 | 388,0544 | 2175,095 |
| 397,7 | 1482,8 | 1298,184 | 1080,471 | 1515,897 | 405,567 | 2190,8 |
| 450,7 | 1151,7 | 1365,381 | 1161,528 | 1569,234 | 476,0433 | 2254,719 |
| 457,6 | 1020,6 | 1374,129 | 1171,951 | 1576,308 | 485,1738 | 2263,085 |
| 515,3 | 1447,286 | 1257,755 | 1636,816 | 561,1213 | 2333,45 | |
| 533,8 | 2441,9 | 1470,741 | 1284,706 | 1656,777 | 585,3178 | 2356,165 |
| 587,8 | 1424,6 | 1539,207 | 1361,598 | 1716,815 | 655,5153 | 2422,898 |
| 614,9 | 1095,4 | 1573,566 | 1399,104 | 1748,028 | 690,5016 | 2456,63 |
| 655,1 | 1278,5 | 1624,535 | 1453,293 | 1795,776 | 742,1008 | 2506,968 |
| 720,1 | 2091,4 | 1706,946 | 1537,058 | 1876,835 | 824,7741 | 2589,119 |
| 741,5 | 2403,5 | 1734,079 | 1563,573 | 1904,585 | 851,7875 | 2616,37 |
| 760,9 | 1758,676 | 1587,159 | 1930,192 | 876,1885 | 2641,163 | |
| 814,1 | 2042,3 | 1826,126 | 1649,714 | 2002,539 | 942,6747 | 2709,578 |
| 859,2 | 1607,9 | 1883,308 | 1700,459 | 2066,156 | 998,5482 | 2768,067 |
| 1683,2 | 1974,341 | 1777,47 | 2171,211 | 1086,578 | 2862,104 | |
| 953,8 | 2003,248 | 1801,083 | 2205,414 | 1114,296 | 2892,201 | |
| 1092,6 | 3063,9 | 2179,229 | 1938,135 | 2420,324 | 1280,624 | 3077,835 |
| 1148,9 | 2048,4 | 2250,611 | 1991,234 | 2509,988 | 1346,928 | 3154,293 |
| 1247,5 | 2034,4 | 2375,623 | 2081,869 | 2669,377 | 1461,48 | 3289,766 |
| 1253,1 | 2435,9 | 2382,723 | 2086,944 | 2678,503 | 1467,927 | 3297,519 |
| 1873,5 | 3082,1 | 3169,312 | 2625,412 | 3713,212 | 2146,966 | 4191,659 |
Графически доверительные границы для у представляют собой гиперболы, расположенные по обе стороны от линии регрессии (рис.6).
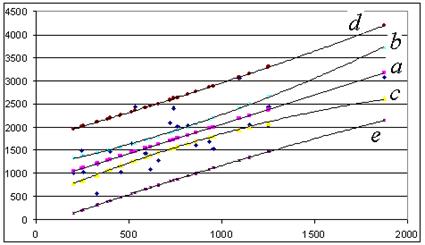
Рис. 6. Доверительный интервал линии регрессии:
а - линия регрессия ух = b0 + b1х;
b, c - верхняя и нижняя границы доверительного интервала для ур;
d, e - доверительный интервал для индивидуальных значений у
Индивидуальное задание № 1 для контрольной работы
Парный регрессионный анализ
Построить диаграммы рассеяния. Определить выборочную ковариацию, среднее квадратическое отклонение для величин X и Y, выборочную дисперсию переменной Х, коэффициенты уравнения регрессии, коэффициент корреляции, выборочную остаточную дисперсию, 95% доверительный интервал для функции регрессии, 95% доверительный интервал для индивидуальных значений зависимой переменной (значение из середины таблицы – 6-я сторока), 95% доверительный интервал для параметров регрессионной модели (для коэффициента регрессии, для дисперсии и для среднего квадратического отклонения случайной составляющей), коэффициент детерминации. Оценить значимость уравнения регрессии, значимость коэффициентов регрессии, значимость коэффициента корреляции. Принять уровень значимости а = 0,05.
Вариант 1.
Имеются данные о количестве слесарей-ремонтников на предприятиях области и данные о количестве станко-смен:
| количество слесарей-ремонтников | количество станко-смен |
| 0,8 | |
| 0,5 | |
| 0,8 | |
| 0,8 | |
| 0,8 | |
| 2,2 | |
| 1,4 | |
| 2,3 | |
| 6,4 | |
| 1,1 | |
| 6,3 |
Вариант 2.
Имеются данные о количестве слесарей-ремонтников на предприятиях области и данные о количестве единиц ремонтной сложности:
| количество слесарей-ремонтников | количество единиц ремонтной сложности |
| 6,1 | |
| 4,4 | |
| 3,5 | |
| 3,1 | |
| 3,5 | |
| 4,9 | |
| 6,8 | |
| 18,4 | |
| 19,6 | |
| 5,8 | |
| 10,4 |
Вариант 3.
Имеются данные об объеме выпускаемой продукции и ее себестоимости:
| объем выпускаемой продукции, тыс.шт | Себестоимость, ден.ед. |
| 3,9 | |
| 2,8 | |
| 4,8 | |
| 3,1 | |
| 3,2 | |
| 3,3 | |
| 3,4 | |
| 3,5 | |
| 3,7 | |
Вариант 4.
Имеются данные о среднемесячной производительности рабочего на шахте в метрах и себестоимости угля в ден.ед за тонну:
| производительность рабочего | себестоимость |
| 1,3 | |
| 1,2 | |
| 1,3 | |
| 1,1 | |
| 1,1 | |
| 1,1 | |
| 1,4 | |
| 1,7 |
Вариант 5.
Имеются данные о среднегодовой численности работников и сумме производственных затрат на предприятиях:
| численность работников | производственные затраты |
Вариант 6.
Имеются данные о выработке на одного работающего и фондовооруженности:
| выработка | фондовооруженность |
| 3,3 | 1,9 |
| 4,6 | |
| 3,4 | 2,2 |
| 5,5 | 2,3 |
| 2,4 | |
| 5,1 | 2,4 |
| 2,6 | |
| 4,2 | 2,6 |
| 3,8 | 2,6 |
| 5,1 | 2,7 |
| 4,8 | 2,8 |
Вариант 7.
Имеются данные об уровне издержек обращения и грузообороте предприятия:
| Уровень издержек обращения, руб/т | Грузооборот, тыс. т |
| 2,72 3,04 2,84 2,74 2,72 2,64 2,52 2,75 2,63 2,62 2,62 | 15,6 13,5 15,3 14,9 15,1 16,1 16,7 15,4 17,1 16,8 16,9 |
Вариант 8.
Имеются данные о браке литья (в %) и себестоимости одной тонны литья (в ден.ед.) по заводам:
| брак | себестоимость |
| 4,2 6,7 5,5 7,7 1,2 2,2 8,4 1,4 4,2 0,9 1,3 |
Вариант 9.
Имеются данные о товарообороте (в ден. ед.) и среднем числе потребителей в день (в тыс. чел.):
| Годовой товарооборот | Среднее число посетителей в день |
| 19,76 38,09 40,95 41,08 56,29 68,51 75,01 89,05 91,13 91,26 99,84 | 8,25 10,24 9,31 11,01 8,54 7,51 12,36 10,81 9,89 13,72 12,27 |
Вариант 10.
Имеются данные о выработке продукции на одного работника (тыс, руб.) и удельном весе рабочих высокой квалификации в общей численности рабочих (%).
| выработка | рабочие |
| 3,9 3,9 3,7 4,0 3,8 4,8 5,4 4,4 5,3 6,8 6,0 | 7,0 7,0 7,0 7,0 7,0 7,0 8,0 8,0 8,0 10,0 9,0 |
Пример задания № 2. Провести оценку параметров уравнения связи для многофакторной модели, проверить значимость и адекватность полученного уравнения и каждого из его параметров. Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 70% от их максимальных значений.. Принять уровень значимости a = 0,05.
Найти 95% доверительные интервалы для параметров уравнения. Провести анализ на мультиколлинеарность. Определить и проанализировать частные коэффициенты корреляции. Вычислить коэффициент множественной корреляции и коэффициент детерминации и проанализировать их. Определить и проанализировать частные коэффициенты эластичности.
Исходные данные для расчёта
| Предприятие | Мощность пласта, м Х1 | Уровень механизации, % Х2 | Сменная добыча на одного работника, т У |
1. Построение линейной зависимости на основе поля корреляции
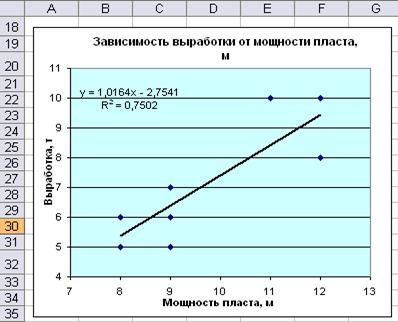
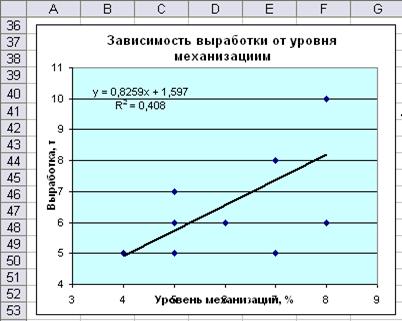
2. Определение параметров уравнения регрессии в матричной форме B=(Х’X)-1X’Y
Сформировать матрицу Х объясняющих переменных размером 10х3, добавив столбец с единичными элементами перед столбцами данных по факторным переменным. Этот столбец получается как единичное значение переменной х 0, умножаемой на коэффициент b 0. Столбец зависимой переменной составляет вектор Y.
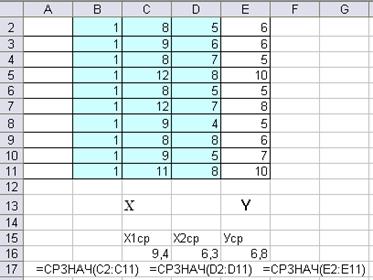
Определим с помощью функции =ТРАНСП (из категории Ссылки и массивы) транспонированную матрицу Х’. Для этого выделим массив ячеек 3х10 и введём в него функцию транспонирования, указав в качестве аргументов исходную матрицу Х, включающую и первый столбец из единиц. Для получения массива результатов по этой функции следует в завершении нажать комбинацию клавиш Ctrl+Shift+Enter или же повторить эту комбинацию при активизации строки формул (щёлкнуть левой кнопкой мыши в строке формул).
Перемножим транспонированную матрицу X ’ с исходной матрицей Х, используя функцию =МУМНОЖ из категории математические. Для вывода результатов предварительно должен быть выделен массив ячеек 3х3. Полученная матрица должна быть симметричной.
Найдём обратную матрицу (X’X)-1, используя математическую функцию =МОБР, аргументом которой является матрица X’X. Поскольку результат также представляет собой симметричную матрицу 3-го порядка, то предварительно необходимо выделить массив ячеек 3х3.
Умножим транспонированную матрицу Х’ на вектор Y, выделив для этого столбец из трёх ячеек.
Перемножение результатов этих действий (обратной матрицы (X’X)-1 на вектор Х’Y) даёт вектор коэффициентов уравнения регрессии В. Для получения массива результатов по всем этим функциям следует нажать комбинацию клавиш Ctrl+Shift+Enter.
Уравнение регрессии имеет вид:
= -3,5393 + 0,85393 х 1 + 0.6704 х 2
3. Анализ на наличие мультиколлинеарности. Используем функцию =КОРРЕЛ для определения парных коэффициентов корреляции. Поскольку коэффициент корреляции между х 1 и х 2 равен 0,48768, что меньше 0,8, проблема коллинеарности факторов отсутствует. В тоже время, коэффициенты парной корреляции между факторами и результирующей переменной У имеют высокие значения (0,86614 и 0,63876), что свидетельствует об их тесной зависимости.
4. Для определения влияния параметров уравнения регрессии на зависимую величину, найдём средние арифметические значения всех переменных с помощью функции =СРЗНАЧ. Определим также средние значения переменных, возведённых в квадрат и используем для расчёта дисперсий факторных переменных и результирующей переменной
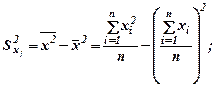
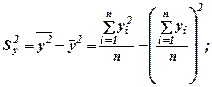
S 2 x 1= 2,44, S 2 x 2= 2,01 S 2y= 3,36
Определим средние квадратические отклонения
Sx 1= 1,56205, Sx 2= 1,41774 S y= 1,83303
Определим стандартизованные коэффициенты регрессии
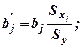
b’1= 0,72769 b’2=0,28389
Таким образом, увеличение мощности пласта и уровня механизации работ только на одно среднее квадратическое отклонение Sx1 и Sx2 увеличит сменную добычу угля на 0,72769Sy и 0.28389Sy соответственно.
Определим коэффициенты эластичности
E1= 1,18044 E2= 0,34005
Увеличение этих переменных на 1% от своих средних значений приводит в среднем к росту добычи угля соответственно на 1,18% и 0,34%. На сменную добычу угля большее влияние оказывает фактор мощности пласта.
5. Определим суммы квадратов отклонений, дисперсии на степень свободы и средние квадратические отклонения (общие, объяснённые регрессией и остаточные)
=33,6;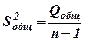 
=3,73333; Sобщ=1,96218
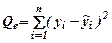=6,32959; 
=0,90423; S=0,95091
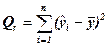=33,6 – 6,32989 = 27,2704; 
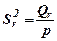= 13,6352;
Sr = 3,69259
Определим дисперсии и средние квадратические отклонения для параметров уравнения регрессии, используя диагональные элементы обратной матрицы (X’X)-1
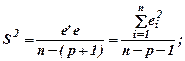
Sbo=1,90658; Sb1= 0.2205; Sb2= 0.24295
Определим значения t-статистики Стьюдента
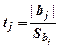; t 0 = 1,85637; t 1 = 3,87263; t 2 = 1,51078
Критическое (табличное) значение критерия Стьюдента определяется с помощью функции =СТЬЮДРАСПОБР, в качестве аргументов которой вводится вероятность – уровень значимости α = 0,05 и число степеней свободы df = n – p – 1.
t крит = 2,36462, следовательно, значимым оказался только коэффициент b1, а b0 и b2 – статистически незначимы. Таким образом в модели следует отказаться от использования фактора x2 и константы b0.
Определим Р -значение, вероятность ошибки с помощью функции =СТЬЮДРАСП, аргументами которой являются: расчётное значение t-статистики, число степеней свободы df = n – p – 1, хвосты = 2.
P(b0) = 0,10577; P(b1) = 0,00611; P(b2) = 0,1746
Вероятность ошибки не должна превышать 0,05. Вероятность ошибки по коэффициенту b0 – более 10%, b1 – менее 0,6% и b2 – более 17%. Это подтверждает значимость только коэффициента b1.
6. Определим 95%-ные доверительные интервалы для коэффициентов регрессии, теоретической линии регрессии, индивидуальных значений и дисперсии. Допустим 70%-ные значения от максимальных величин факторов равны х1 = 8, х2 = 6. Определим расчётное значение функции для этих значений
= -3,5393 + 0,85393 х 1 + 0.6704 х 2 = -3,5393 + 0,85393×8 + +0.6704×6 = 5,49438.
Определим стандартное отклонение для линии регрессии.
Для этого умножим вектор Х’ 0 = (1 8 6) на обратную матрицу (X’X)-1, выделив строку из трех ячеек. Результат (0,5947 -0,0666 0,02087) умножим на вектор-столбец Х 0. В результате получим значение 0,187. Стандартное отклонение равно 0,4112.
Стандартное отклонение для индивидуальных значений
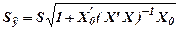= 1,03601.
Определим доверительные интервалы для коэффициентов уравнения регрессии
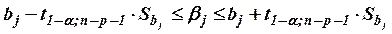
Для коэффициентов β 0 и β 2 доверительные интервалы накрывают диапазон от отрицательных значений до положительных, включая и 0 (-8,0477 £ β 0 £ 0,96902 и -0,2074 £ β 2 £ 0,94152). Поэтому достоверно нельзя судить о том влияет данный фактор отрицательно, положительно или вообще не влияет на результирующую переменную, - невозможно. Это подтверждает статистическую незначимость данных коэффициентов. Истинное значение коэффициента β1 с вероятностью 95% лежит в пределах от 0,33252 до 1,37534.
Определим доверительный интервал для линии регрессии
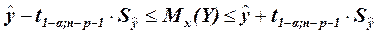
С вероятностью 95% выработка на одного работающего для предприятий с мощностью пласта 8 м и уровнем механизации 6% лежит в пределах 4,52204 £ Mx(Y) £ 6,46673 тонн.
Определим доверительный интервал для индивидуальных значений
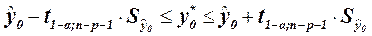
С вероятностью 95% индивидуальные значения выработки на одного работающего для предприятий с мощностью пласта 8 м и уровнем механизации 6% лежит в пределах 3,04461 £y0*£7,94416 тонн.
Определим доверительный интервал для дисперсии
Значения величин ХИ-квадрат распределения определим с помощью функции =ХИ2ОБР. Истинное значение дисперсии с вероятностью 95% лежит в пределах 0,56469£s2£5,35087.
7. Определим значимость модели в целом
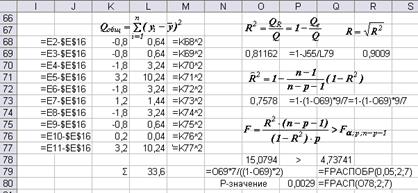
Выборочный коэффициент множественной детерминации рассчитывается по формуле
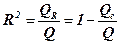= 0,81162 
,
где 
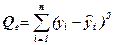
Полученное значение показывает, что на 81,16% с помощью линейного уравнения множественной регрессии удалось объяснить вариацию зависимой переменной влиянием включённых факторов. Оставшиеся 18,84% - влиянием неучтённых в модели и случайных факторов.
Выборочный множественный коэффициент корреляции 
= 0,9009 свидетельствует о высокой степени зависимости между результирующей переменной и влияющими на неё факторами.
Скорректированный (адаптированный) коэффициент детерминации равен
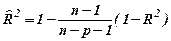= 0,7578.
Полученное значение характеризует значимость уравнения регрессии в целом.
Оценим статистическую значимости полученного уравнения регрессии в целом с помощью F-критерия Фишера. Уравнение множественной регрессии значимо ил нулевая гипотеза Но о равенстве нулю параметров регрессионной модели, т.е. Н о: β 1= β 2= …= β р= 0 отвергается, если
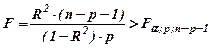
Расчётное значение F -статистики 15,0794, критическое значение для доверительного уровня
γ = 0,95 (уровня значимости α = 0,05) определяется с помощью статистической функции =FРАСПОБР (α; р; n – p – 1). F кр = 4,73741. Поскольку расчётное значение критерия Фишера больше критического (табличного) значения, то с вероятностью 95% уравнение статистически значимо.
Определим значимость F -статистики (вероятность ошибки) с помощью функции =FРАСП (F; p; n – p – 1) = 0,0029. Поскольку полученное значение меньше величины α = 0,05, вывод о значимости уравнения регрессии подтверждается.
Но поскольку данное уравнение содержит и незначимые параметры, использование его как многофакторной модели может привести к неверным выводам при анализе ситуации и прогнозировании её развития.
Варианты индивидуального задания № 2 по
