Не параметрические критерии Уайта и Вилкоксона.
t-критерий Стьюдента - общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
Требования к данным
Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.
Двухвыборочный t-критерий для независимых выборок
В случае с незначительно отличающимся размером выборки применяется упрощённая формула приближенных расчётов:
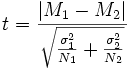
В случае, если размер выборки отличается значительно, применяется более сложная и точная формула:

Где M 1, M 2 - средние арифметические, σ1,σ2 - стандартные отклонения, а N 1, N 2 - размеры выборок.
Количество степеней свободы рассчитывается как

Двухвыборочный t-критерий для зависимых выборок
Для вычисления эмпирического значения t-критерия в ситуации проверки гипотезы о различиях между двумя зависимыми выборками (например, двумя пробами одного и того же теста с временным интервалом) применяется следующая формула:

где Md - средняя разность значений, а σ d - стандартное отклонение разностей.
Количество степеней свободы рассчитывается как

Одновыборочный t-критерий
Применяется для проверки гипотезы об отличии среднего значения  от некоторого известного значения
от некоторого известного значения  :
:
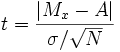
Количество степеней свободы рассчитывается как

Непараметрические аналоги
Аналогом двухвыборочного критерия для независимых выборок является U-критерий Манна-Уитни. Для ситуации с зависимыми выборками аналогами являются критерий знаков и T-критерий Вилкоксона
Критерий Фишера (F-критерий, φ*-критерий, критерий наименьшей значимой разности) — апостериорный статистический критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть для определения значимых различий между групповыми средними в установке дисперсионного анализа.
W-Критерий Вилкоксона — непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных измерений. Впервые предложен Фрэнком Уилкоксоном.
Назначение критерия
Критерий предназначен для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность, то есть, способен определить, является ли сдвиг показателей в одном направлении более интенсивным, чем в другом.
Описание критерия
Критерий применим в тех случаях, когда признаки измерены, по крайней мере, в порядковой шкале. Целесообразно применять данный критерий, когда величина самих сдвигов варьирует в некотором диапазоне (10-15% от их величины). Это объясняется тем, что разброс значений сдвигов должен быть таким, чтобы появлялась возможность их ранжирования. В случае если сдвиги незначительно отличаются между собой, и принимают какие-то конечные значения, например. +1, -1 и 0, формальных препятствий к применению критерия нет, но, ввиду большого числа одинаковых рангов, ранжирование утрачивает смысл, и те же результаты проще было бы получить с помощью критерия знаков.
Суть метода состоит в том, что мы сопоставляем абсолютные величины выраженности сдвигов в том или ином направлении. Для этого сначала все абсолютные величины сдвигов ранжируются, а потом суммируются ранги. Если сдвиги в ту или иную сторону происходят случайно, то и суммы их рангов окажутся примерно равны. Если же интенсивность сдвигов в одну сторону больше, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.
Ограничения критерия
Объем выборки — от 5 до 50 элементов.
Нулевые сдвиги исключаются из рассмотрения. (Это требование можно обойти, переформулировав вид гипотезы. Например: сдвиг в сторону увеличения значений превышает сдвиг в сторону их уменьшения и тенденцию к сохранению на прежнем уровне.)
Сдвиг в более часто встречающемся направлении принято считать «типичным», и наоборот.
Есть также урезанный вариант для сравнения одной выборки с известным значением медианы.
Алгоритм
1. Составить список испытуемых в любом порядке, например, алфавитном.
2. Вычислить разность между индивидуальными значениями во втором и первом замерах. Определить, что будет считаться типичным сдвигом.
3. Согласно алгоритму ранжирования, проранжировать абсолютные величины разностей, начисляя меньшему значению меньший ранг, и проверить совпадение полученной суммы рангов с расчетной.
4. Отметить каким-либо способом ранги, соответствующие сдвигам в нетипичном направлении. Подсчитать их сумму Т.
5. Определить критические значения Т для данного объема выборки. Если Т-эмп. меньше или равен Т-кр. – сдвиг в «типичную» сторону достоверно преобладает.
Фактически оцениваются знаки значений, полученных вычитанием ряда значений одного измерения из другого. Если в результате количество снизившихся значений примерно равно количеству увеличившихся, то гипотеза о нулевой медиане подтверждается.






