На этапе статистической обработки могут быть поставлены самые различные задачи исследования, для решения которых нужно выбрать соответствующую среднюю. При этом необходимо руководствоваться следующим правилом: величины, которые представляют собой числитель и знаменатель средней, должны быть логически связаны между собой.
Используются две категории средних величин:
o степенные средние;
o структурные средние.
Первая категория степенных средних включает: 
среднюю арифметическую, среднюю гармоническую, среднюю квадратическую и среднюю геометрическую.
Вторая категория (структурные средние) - это мода и медиана.
Введем следующие условные обозначения:
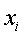- величины, для которых исчисляется средняя;
- средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;
- частота (повторяемость индивидуальных значений признака).
Различные средние выводятся из общей формулы степенной средней:
(5.1)
при k = 1 - средняя арифметическая; k = -1 - средняя гармоническая; k = 0 - средняя геометрическая; k = -2 - средняя квадратическая.
Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту f называют статистическим весом или весом средней.
Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.
Формула средней арифметической (простой) имеет вид
(5.2)
где n - численность совокупности.
Например, средняя заработная плата работников предприятия вычисляется как средняя арифметическая:
Определяющими показателями здесь являются заработная плата каждого работника и число работников предприятия. При вычислении средней общая сумма заработной платы осталась прежней, но распределенной как бы между всеми работниками поровну. К примеру, необходимо вычислить среднюю заработную плату работников небольшой фирмы, где заняты 8 человек:
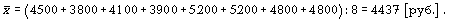
При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид
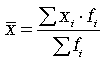(5.3)
Так, нам необходимо рассчитать средний курс акций какого-то акционерного общества на торгах фондовой биржи. Известно, что сделки осуществлялись в течение 5 дней (5 сделок), количество проданных акций по курсу продаж распределилось следующим образом:
1 - 800 ак. - 1010 руб.
2 - 650 ак. - 990 руб.
3 - 700 ак. - 1015 руб.
4 - 550 ак. - 900 руб.
5 - 850 ак. - 1150 руб.
Исходным соотношением для определения среднего курса стоимости акций является отношение общей суммы сделок (ОСС) к количеству проданных акций (КПА):
ОСС = 1010 ·800+990·650+1015·700+900·550+1150·850= 3 634 500;
КПА = 800+650+700+550+850=3550.
В этом случае средний курс стоимости акций был равен
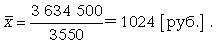
Необходимо знать свойства арифметической средней, что очень важно как для ее использования, так и при ее расчете. Можно выделить три основных свойства, которые наиболее всего обусловили широкое применение арифметической средней в статистико-экономических расчетах.
Свойство первое (нулевое): сумма положительных отклонений индивидуальных значений признака от его среднего значения равна сумме отрицательных отклонений. Это очень важное свойство, поскольку оно показывает, что любые отклонения (как с +, так и с -), вызванные случайными причинами, взаимно будут погашены.
Доказательство:
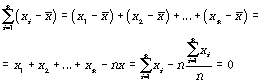
Свойство второе (минимальное): сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа (а), т.е. есть число минимальное.
Доказательство.
Составим сумму квадратов отклонений от переменной а:
(5.4)
Чтобы найти экстремум этой функции, необходимо ее производную по а приравнять нулю:
Отсюда получаем:
(5.5)
Следовательно, экстремум суммы квадратов отклонений достигается при 
. Этот экстремум - минимум, так как функция не может иметь максимума.
Свойство третье: средняя арифметическая постоянной величины равна этой постоянной: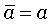 
при а = const.
Кроме этих трех важнейших свойств средней арифметической существуют так называемые расчетные свойства, которые постепенно теряют свою значимость в связи с использованием электронно-вычислительной техники:
o если индивидуальное значение признака каждой единицы умножить или разделить на постоянное число, то средняя арифметическая увеличится или уменьшится во столько же раз;
o средняя арифметическая не изменится, если вес (частоту) каждого значения признака разделить на постоянное число;
o если индивидуальные значения признака каждой единицы уменьшить или увеличить на одну и ту же величину, то средняя арифметическая уменьшится или увеличится на ту же самую величину.
Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.
Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:
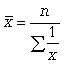(5.6)
К примеру, нам нужно вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая - со скоростью 100 км/ч, вторая - 90 км/ч. Применяя метод средней гармонической, мы вычисляем среднюю скорость:
В статистической практике чаще используется гармоническая взвешенная, формула которой имеет вид
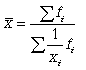(5.7)
Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. В исходном соотношении для расчета средней известен числитель, но неизвестен знаменатель.
Например, при расчете средней цены мы должны пользоваться отношением суммы реализации к количеству реализованных единиц. Нам не известно количество реализованных единиц (речь идет о разных товарах), но известны суммы реализаций этих различных товаров. Допустим, необходимо узнать среднюю цену реализованных товаров:
| Вид товара | Цена за единицу, руб. | Сумма реализаций, руб. |
| а | ||
| б | ||
| с |
Получаем
Если здесь использовать формулу средней арифметической, то можно получить среднюю цену, которая будет нереальна:
Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической.
Для простой средней геометрической
Для взвешенной средней геометрической
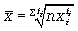(5.9)
Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).
Формула простой средней квадратической
(5.10)
Формула взвешенной средней квадратической
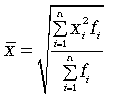(5.11)
В итоге можно сказать, что от правильного выбора вида средней величины в каждом конкретном случае зависит успешное решение задач статистического исследования. Выбор средней предполагает такую последовательность:
а) установление обобщающего показателя совокупности;
б) определение для данного обобщающего показателя математического соотношения величин;
в) замена индивидуальных значений средними величинами;
г) расчет средней с помощью соответствующего уравнения.
