Програмні питання
Понятті про структурну надійність схем електричних систем. Стан повної відмови і безвідмовної роботи схем. Структурний аналіз і формальні прийоми декомпозицій складних схем. Показники надійності відносно вузлів навантаження в складних схемах.
Теоретичні відомості
При ознайомленні з матеріалом по даній темі необхідно вивчити методи аналізу надійності складних структур електричних систем, вдосконалити знання про структурну надійність схем електричних систем, а також вміти аналізувати стан повної відмови і безвідмовної роботи схем, проводити структурний аналіз і формальні прийоми декомпозицій складних схем.
При вивченні матеріалу по даній темі студентам необхідно ознайомитись з графічним матеріалом, який представлений в конспекті лекцій з математичного моделювання систем електропостачання та підручниках.
Запитання для самоперевірки
1. Що називають структурною надійністю?
2. Що називають функціональною надійністю?
3. Що називають шляхами схеми? Як складається матриця шляхів?
4. Що називають мінімальним перерізом схеми? Як складається матриця перерізів?
5. Які правила логічного додавання?
6. За якою формулою визначається ймовірність відмови перерізів?
7. Як визначається надійність електропостачання вузла навантаження складної схеми?
8. Наведіть приклад побудови матриці перерізів та матриці шляхів.
9. Який принцип визначення мінімальних перерізів в різних станах схеми?
Приклади розрахунків
Задача №1
Система електропостачання підпорядковується нормальному закону розподілу напрацювання до відмови з параметрами ТМ = 1200 год і σ =250 год. Можливі значення напрацювання до відмови знаходяться в інтервалі (0÷∞). Протягом якого часу t система буде функціонувати з ймовірністю не менш ніж Р(t)=0,95.
Розв'язок
Оскільки час безвідмовної роботи знаходиться в (0÷∞) то йдеться про зрізаний нормальний закон нормальний закон розподілу для якого:
 .
.
де нормуючий множник:
 .
.
Знайдено функцій Лапласа з виразу для Р(t):
 .
.
Через неперервність функції Лапласа знайдено з таблиць аргумент  , якому відповідає значення функції 0,45. Отримуємо:
, якому відповідає значення функції 0,45. Отримуємо:
 ,
,
Звідси 
Задача №2
Знайти ймовірність безвідмовної роботи системи, логічна схема з’єднань якої показана на рисунку 1.1:

Рисунок 1.1 – Розрахункова схема
Розв'язок
На логічній схемі можна виділити дві групи:
– І – логічне послідовне з’єднання;
– ІІ – логічне паралельне з’єднання.
Між собою І ті ІІ з’єднані логічно послідовно, тому 
 ,
,
 .
.
Остаточно отримаємо:
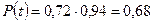 .
.
Задача №3
Перемикачі А, В, С і D в приведеній схемі (рис. 1.2) працюють незалежно один від одного. Необхідно визначити ймовірність протікання струму І через схему, якщо ймовірність замкнутого стеку кожного перемикача рівна 0,2.

Рисунок 1.2 – Розрахункова схема
Розв'язок
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Задача №4
Якою повинна бути ймовірність безвідмовної роботи кожного з п’яти рівнонадійних елементів, щоб при їх логічному паралельному з’єднанні система мала ймовірність безвідмовної роботи не менше ніж 0,95.
Розв'язок
Запишемо ймовірність безвідмовної роботи системи:
 .
.
З цього виразу отримаємо:
 .
.
Задача №4
Визначити конструкційну надійність двигуна постійного струму типа ПН-100 для трьох проміжків часу його роботи: t = 1000, 3000 і 5000 год, за наступними середніми статистичними даними про інтенсивність відмов основних її частин в долях одиниці на одну годину роботи: магнітна система з обмоткою збудження – λ 1 ≈ 0,01·10-6; обмотка якоря – λ 2 ≈ 0,05·10-6; підшипники ковзання – λ 3 ≈ 0,4·10-6; колектор – λ 4 ≈ 3·10-6 і щітковий пристрій – λ 5 ≈ 1·10-6 год-1.
Розв'язок
Визначаємо середню результуючу інтенсивність відмов всіх частин двигуна:
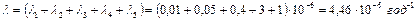 .
.
Середнє напрацювання до першої відмови двигуна:
 .
.
Ймовірність безвідмовної роботи даного двигуна для трьох проміжків часу:
 ;
;
 ;
;
 .
.
Як видно з одержаних даних, конструкційна надійність розглянутого двигуна постійного струму характеризується тим, що на кожні 1000 двигунів ймовірність виходу з ладу протягом вказаних трьох проміжків часу роботи складає: у першому випадку – 5 двигунів, або 0,5%; у другому – 12 двигунів, або 1,2%; і в третьому – 25 двигунів, або 2,5%.






