| 1. Задан граф V=(1,2,3,4) Е=(a, b, c, d), Постройте граф и его матрицы смежности и инцидентности. | ||||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение с): матрица смежности А=
|
матрица инцидентности В=
| |||||||||||||||||||||||||||||||||||||||||||||||||||
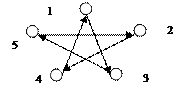
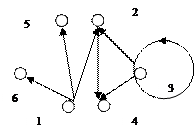
2. Графы G1(V1,E1) и G2(V2,E2) заданы геометрически.
Постройте:
а) для графаG1(V1,E1) матрицу смежности,
б) для графаG2(V2,E2) матрицу смежности и матрицу инцидентности.
 Решение:
Матрица смежности:
Вершины графа v1v2v3v4
А(G) =
Решение:
Матрица смежности:
Вершины графа v1v2v3v4
А(G) = 
|

e4 e5 e6
e7
Решение: Матрицы смежности и инцидентности: Вершины графа А(G) = |
Задания для самостоятельного выполнения
Постройте для графа G(V,E), заданного геометрически,
А) матрицу смежности; б) матрицу инцидентности.
0)
| 1)

| |||||||||||||||||
2)

| 3)              | |||||||||||||||||
4)
 
| 5)           
| |||||||||||||||||
6)
| 7)
| |||||||||||||||||
8)

| 9)  
|
5.
|
Матрицу смежности и матрицу инцидентности.
Подсчитайте валентность вершин.
Определите тип графа.
| |||
| |||
|
|
|

|

Ориентированные графы
Ориентированный граф (или орграф) G1 (V, E) – непустое конечное множество узлов (вершин) V и набор упорядоченных пар вершин (дуг) E.
Пусть v 1, v 2,... vn - вершины графа G1 (V, E), а e 1, e 2,... em - его дуги.
Матрицей смежности графа G1 называется матрица A(G1)= || aij ||, i =1,..., n; j = 1,..., n, у которой элемент aij равен числу дуг, соединяющих вершины vi и vj (соответственно, идущих из вершины vi в вершину vj).
Свойства матрицы смежности:
1) несимметричная, в общем случае, относительно главной диагонали,
2) значениями являются натуральные числа и ноль,
3) количество петель записывается на главной диагонали,
4) сумма значений по строке (столбце) равна валентности вершины.
Матрицей инцидентности для ориентированного графа с n вершинами и m дугами называется матрица В(G1) = [bij], i=1, 2,..., n, j = 1,2,..., m, строки которой соответствуют вершинам, а столбцы - дугам.
Ее элемент: bij=1, если дуга еi выходит из вершины vj; bij= -1, если дуга ei входит в вершины vj; bij=0, если вершина vj не инцидентна дуге еi.
Свойства матрицы инцидентности:
1) несимметричная, 2) значениями являются -1, ноль и 1.
Примеры выполнения заданий
1. Орграф G1(V,E) задан геометрически. Постройте для орграфа:
А) матрицу смежности; б) матрицу инцидентности.
     
      
| Решение а): матрица смежности А(G1)=
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение б): матрица инцидентности В(G1)=
|
Задания для самостоятельного выполнения
Орграф задан геометрически. Укажите валентность вершин.Постройте матрицу смежности орграфа.
0)
|
| ||||||||||||||||||||||
2) 

| 3)  
| ||||||||||||||||||||||
4) 

| 5)                    
| ||||||||||||||||||||||
6)
| 7)
| ||||||||||||||||||||||
8)
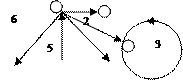
| 9)              
|
Дана матрица смежности орграфа. а) Задайте орграф геометрически, в) постройте матрицу инцидентности.
0)  1)
1)  2)
2)  3)
3)  4)
4) 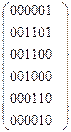
5) 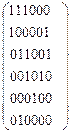 6)
6)  7)
7)  8)
8)  9)
9) 
Запишите: 1) любой путь, не являющийся цепью; 2) цепь и простую цепь; 3) цикл, простой цикл, если таковые имеются.

Практическое занятие №3.
Комбинаторика.






 e1 e2 e3
e1 e2 e3

 В(G) =
В(G) =