Плазма – частично или полностью ионизированный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы. В самом простом случае плазму можно рассматривать как квазинейтральный разреженный газ, состоящий из электронов и ионов. Воздействие на плазму электромагнитным полем приводит к движению свободных зарядов и возникновению электрического тока. Токи и заряды образуют собственное ЭМП. Поскольку масса ионов значительно больше массы электронов, считаем их неподвижными при не слишком больших частотах поля E и рассматриваем только движение электронов.
Вычислим диэлектрическую проницаемость плазмы, считая её холодной (тепловым движением частиц можно пренебречь) и изотропной (свойства среды во всех направлениях не изменяются). Составим уравнение движения электронов в поле монохроматической волны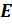 
= 
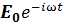. Такое уравнение имеет вид
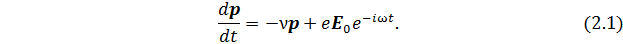
Здесь ν – эффективная частота соударений, p = m v – импульс частиц. Поскольку мы рассматриваем нерелятивистский случай, когда скорости движения частиц значительно меньше скорости света в вакууме, то можно считать движение частиц таковым, что не зависит от индукции магнитного поля электромагнитной волны. Ток и вектор поляризации зависят только от вектора электрического поля E. Решение уравнения (2.1) выглядит так:
v = 
Плотность тока, вектор поляризации, создаваемый электронами, вычислим согласно формулам
, 
, (2.4 – 2.5)
или, с учетом определений закона Ома в дифференциальной форме и вектора поляризации (см. 1.8), имеем:
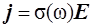
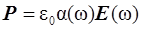. (2.4 – 2.5a)
Отсюда находим комплексную проводимость и комплексную диэлектрическую проницаемость плазмы:
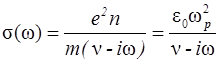, (2.6)
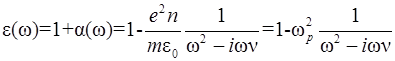. (2.7)
Здесь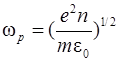 
– частота ленгмюровских колебаний, т. е. электромеханических колебаний с плазменной частотой. Они представляют собой возмущения пространственного заряда, приводящие к обмену энергией между электрическим полем и кинетической энергией
Если плазма помещена в постоянное однородное манитное поле, то ее эффективная диэлектрическая проницаемость больше не является скалярной функцией частоты. Плазма становится анизотропной, свойства её начинают зависеть от направления. Для таких случаев исходными являются уравнения непрерывности, движения, роторные уравнения Максвелла [3].
Рассмотрим однородную покоящуюся плазму с плотностью отрицательных зарядов n 0 в отсутствие электрических полей и токов, на которую действует постоянное однородное магнитное поле B = B 0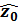 
. Cчитая состояние плазмы слегка возмущенным, запишем уравнение для концентрации:
n = n 0 + n 1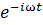 
Вычислим возмущенные величины Е 1, B 1 и V 1, используя уравнения гидродинамики и пренебрегая всеми компонентами, в которые входят произведения возмущенных величин (т. е. нелинейными членами). Запишем эти уравнения.
Уравнение непрерывности:
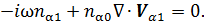
Уравнение движения [3]:
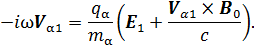
Индекс α, который стоит при скорости распространения колебаний, означает, что данная характеристика пригодна и для электронов, и для ионов; q=e – элементарный заряд; m – масса частицы; индекс 1 указывает на возмущенные поля, 0 – на невозмущенные; ω – циклическая частот колебаний; n α0 – невозмущенная концентрация частиц в единице вещества; n α1 – возмущенная; i – мнимая единица из комплексного анализа, i = 
.
Дополним данную систему роторными уравнениями Максвелла в предположении, что производные по времени заменим на (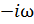
). Такое условие допускается, если каждую из величин, стоящих под знаком производной, представить в виде плоской волны, например 
. Тогда
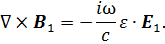
Поскольку среда анизотропная, здесь введен тензор диэлектрической проницаемости
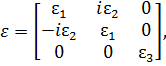
где компоненты записаны следующим образом:
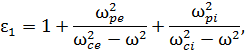
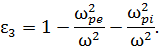
При выводе было учтено, что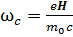 
– циклотронная частота или гирочастота – частота обращения заряженной частицы в постоянном магнитном поле H H {\displaystyle \mathbf {H} } в плоскости, перпендикулярной HH {\displaystyle \mathbf {H} }.
Таким образом мы показали, что в замагниченной плазме P = P (E (ω)) и P =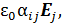 
поэтомудиэлектрическая проницаемость представляет собой тензор II ранга.
