| Зависимость величины А от других величин | Относительная погрешность e | Абсолютная погрешностьD А |
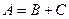
| 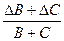
| 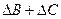
|

| 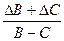
| 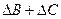
|
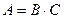
| 
| |
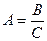
| 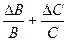
| 
|
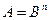
| 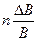
| 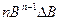
|
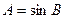
| 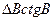
| 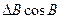
|
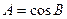
| 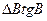
| 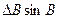
|
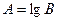
| 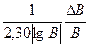
| 
|
Как пользоваться этой таблицей, если функциональная зависимость измеряемых величин в ней отсутствует?
Пусть например, некоторая физическая величина А рассчитывается по формуле: A = 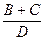 . Значения B, C и D найдены прямыми измерениями во время проведения эксперимента. Их абсолютные погрешности соответственно равны DB, DC и DD. Подставляя полученные значения в формулу, получим приближенное значение Аи. Далее следует рассчитать относительную погрешность результата eА. Это можно сделать, воспользовавшись соответствующими формулами из таблицы 5.
. Значения B, C и D найдены прямыми измерениями во время проведения эксперимента. Их абсолютные погрешности соответственно равны DB, DC и DD. Подставляя полученные значения в формулу, получим приближенное значение Аи. Далее следует рассчитать относительную погрешность результата eА. Это можно сделать, воспользовавшись соответствующими формулами из таблицы 5.
На первый взгляд кажется, что такой формулы в таблице нет. При более внимательном анализе ситуации заметим, что в нашем случае искомое значение находится как отношение двух величин.
Тогда можно воспользоваться формулой А = 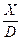 , где X=B+C.
, где X=B+C.
Из таблицы для отношения 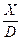 , имеем: eА =eX +eD или eА=eB+C+eD
, имеем: eА =eX +eD или eА=eB+C+eD
В той же таблице найдем как рассчитывать относительную погрешность суммы: eB+C = 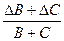 . Следовательно, eА=
. Следовательно, eА= 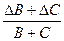 +
+  . Теперь можно найти значение границ абсолютной погрешности, умножив относительную погрешность на величину косвенных измерений: ∆А= (
. Теперь можно найти значение границ абсолютной погрешности, умножив относительную погрешность на величину косвенных измерений: ∆А= (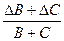 +
+  )∙Аи.
)∙Аи.
Предложите учащимся решить задачи:
Задание 1. Определите объем небольшого тела, например спичечного коробка или бруска, и вычислите интервал значений погрешности измерений двумя методами.
Решение.
а = 5,2 см ± 0,1 см
b = 3,2 см ± 0,1 см
c = 1,5 см ± 0,1 см
Определим объем спичечного коробка, используя формулу V=abc = 5,2 см.3,2 см.1,5 см=24,96 см3
Метод 1. Запишем в виде неравенств:
5,1 см < а < 5,3 см; 3,1 см < b < 3,3 см; 1,4 см < с< 1,6 см
Воспользовавшись формулой V=abc, вычислим наименьшее (Vmin) и наибольшее (Vmax) значенияобъема спичечного коробка:
Vmin = 5,1 см · 3,1см .1,4 см = 22,1 см3 Vmax = 5,2 см · 3,3 см .1,6 см = 27,5 см3
Итак, результат вычисления объема коробка с учётом погрешностей исходных данных в виде неравенства запишется так:
22,1 см3< V< 27,5 см3
Метод 2. Запишем формулу для вычисления относительной погрешности объема спичечного коробка:
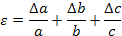
Запишем формулу для вычисления абсолютной погрешности измерения объема спичечного коробка:
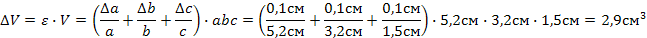
Запишем результат в виде: V = (25,0 ±2,9)см3.

Задание 2. Соберите электрическую цепь по схеме, вычислите сопротивление и определить интервал значений двумя методами.
Решение.
I = 0,4 А±0,1А
U = 3,2В±0,2В
Определим сопротивление резистора (лампы), используя закон Ома для участка цепи
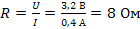
Метод 1. Так как 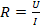 , то нижняя граница значения сопротивления
, то нижняя граница значения сопротивления  ), а верхняясоответственно равна
), а верхняясоответственно равна  Ом
Ом
Или в виде неравенства: 6 Ом < R < 11,3 Ом 
Метод 2. Запишем формулу для вычисления относительной погрешности сопротивления резистора:
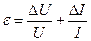
Запишем формулу для вычисления абсолютной погрешности измерения сопротивления резистора:
D R = e × R = 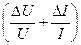 × R =
× R =  × 8 Ом = 2,5 Ом
× 8 Ом = 2,5 Ом
Запишем результат в виде: R = (8,0 ±2,5) Ом.
Заметим, что значение погрешности достаточно велико. Добиться большей точности можно, если использовать амперметр с меньшей ценой деления.
Занятие 5. Лабораторная работа
Цель работы: вычислить ускорение тела, скатывающегося с наклонной плоскости без начальной скорости.
Приборы и материалы: секундомер, измерительная лента (линейка), штатив, желоб, шарик, металлический цилиндр.
Ход работы:
1. Укрепите желоб на штативе, под небольшим углом к горизонту. У нижнего конца желоба положите в него металлический цилиндр.
2. Пустив шарик с верхнего конца желоба, измерьте время его движения вдоль желоба до удара о цилиндр. Повторите опыт 5 раз.
3. С помощью измерительной ленты определите длину перемещения шарика.
4. Вычислите среднее значение времени скатывания шарика и рассчитайте среднее значение модуля ускорения.
Учителю: можно напомнить ученикам формулу вычисления ускорения для равноускоренного движения без начальной скорости: 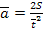
5. Результаты измерений и вычислений запишите в таблицу.
| № опыта | Время скатывания шарика t ± Dt, c | Среднее время скатывания шарика
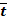 , с , с
| Длина перемещения шарика S ± DS, м | Среднее ускорение `a ± D а, м/с2 |
Указание: при вычислении абсолютных погрешностей измерений и вычислений можете воспользоваться любым методом.
6. Передвиньте цилиндр на середину желоба. Повторите задания п.2-5.
| № опыта | Время скатывания шарика t ± Dt, c | Среднее время скатывания шарика
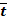 , с , с
| Длина перемещения шарика S ± DS, м | Среднее ускорение `a ± D а, м/с2 |
7. Сделайте вывод.
Образец выполнения лабораторного задания
Ход работы:






