Основы молекулярно-кинетической теории
1. Основное уравнение молекулярно-кинетической теории:
, (2.1)
где n – концентрация молекул газа,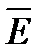 
– средняя кинетическая энергия молекул.
2. Средняя кинетическая энергия молекул:
, (2.2)
где k – постоянная Больцмана, i – число степеней свободы, Т – температура.
3. Количество вещества:
, (2.3)
где N – число частиц в газе, NA – число Авогадро, m – масса газа, μ – молярная масса газа.
4. Плотность газа, занимающего объем V:
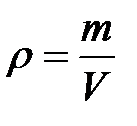. (2.4)
5. Уравнение Менделеева-Клапейрона:
, (2.5)
где P – давление, V – объем газа, μ – молярная масса газа, R – универсальная газовая постоянная, Т – температура газа.
Термодинамика
6. Связь между молярной С и удельной с теплоемкостями:
. (2.6)
7. Молярная теплоемкость при постоянном объеме:
. (2.7)
8. Уравнение Майера:
, (2.8)
где CP – молярная теплоемкость при постоянном давлении
9. Первое начало термодинамики:
, (2.9)
где Q – количество теплоты, сообщенное системе (газу); ΔU – изменение внутренней энергии газа; А – работа, совершенная газом против внешних сил.
10. Изменение внутренней энергии газа:
. (2.10)
11. Работа, совершаемая при изменении объема газа:
. (2.11)
12. Уравнения адиабатического процесса:
; т.е. 
; (2.12)
; т.е. 
. (2.13)
γ – коэффициент Пуассона 
.
13. Коэффициент полезного действия любого термодинамического цикла:
, (2.14)
где А – работа цикла, Q1 – количество теплоты, полученного рабочим телом от нагревателя, или
, (2.15)
где Q2 – теплота, переданная рабочим телом охладителю.
14. Коэффициент полезного действия идеального цикла Карно:
, (2.16)
где Т1 и Т2 – температуры нагревателя и охладителя.
15. Изменение энтропии:
, (2.17)
где А и В – пределы интегрирования, соответствующие начальному и конечному состояниям системы.
Электростатика
1. Закон Кулона:
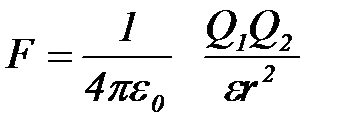, (2.18)
где F – сила взаимодействия точечных зарядов Q1 и Q2; r – расстояние между зарядами; – диэлектрическая проницаемость среды; ε0 – электрическая постоянная.
2. Напряженность электрического поля:
. (2.19)
3. Потенциал электрического поля:
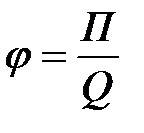, (2.20)
где П – потенциальная энергия точечного положительного заряда Q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).
4. Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей):
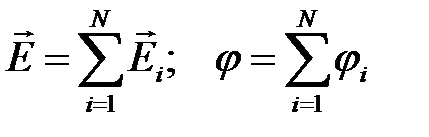, (2.21)
где 
, φi – напряженность и потенциал в данной точке поля, создаваемого i -м зарядом.
5. Напряженность и потенциал поля, создаваемого точечным зарядом:
, (2.22)
где r – расстояние от заряда Q до точки, в которой определяются напряженность и потенциал.
6. Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиуса R на расстоянии r от центра сферы (заряд сферы Q):
· если r<R, то E=0; 
; (2.23)
· если r=R, то 
; 
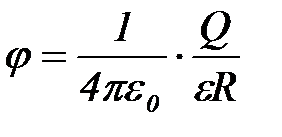; (2.24)
· если r>R, то 
; 
. (2.25)
7. Линейная плотность заряда (заряд, приходящийся на единицу длины заряженного тела):
. (2.26)
8. Поверхностная плотность заряда (заряд, приходящийся на единицу площади поверхности заряженного тела):
. (2.27)
9. Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью τ, то на линии выделяется малый участок длины dl с зарядом dQ=τdl. Такой заряд можно рассматривать как точечный. Напряженность dE и потенциал dφ электрического поля, создаваемого зарядом dQ, определяется формулами:
, (2.28)
где r – радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.
Используя принцип суперпозиции электрических полей, находим интегрированием напряженность 
и потенциал φ поля, создаваемого распределенным зарядом:
. (2.29)
Интегрирование ведется вдоль всей длины l заряженной линии.
10. Напряженность поля, создаваемого бесконечной прямой равномерно заряженной линией или бесконечно длинным цилиндром:
, (2.30)
где r – расстояние от нити или оси цилиндра до точки, напряженность поля в которой вычисляется.
11. Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:
. (2.31)
12. Связь потенциала с напряженностью:
a) в случае однородного поля
; (2.32)
b) в случае поля, обладающего центральной или осевой симметрией:
. (2.33)
13. Работа сил поля по перемещению заряда Q из точки поля с потенциалом φ1 в точку с потенциалом φ2:
. (2.34)
14. Электроемкость:
или 
, (2.35)
где φ – потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U – разность потенциалов пластин конденсатора.
15. Электроемкость плоского конденсатора:
(2.36)
где S – площадь пластины (одной) конденсатора; d – расстояние между пластинами.
16. Электроемкость батареи конденсаторов:
· а) при последовательном соединении: 
; (2.37)
· б) при параллельном соединение: 
, (2.38)
где N – число конденсаторов в батарее.
17. Энергия заряженного конденсатора:
. (2.39)
Постоянный ток
18. Сила тока:
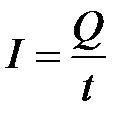, (2.40)
где Q – заряд, прошедший через поперечное сечение проводника за время t.
19. Закон Ома:
а) для участка цепи, не содержащего ЭДС,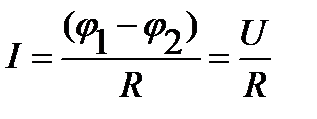 
, (2.41)
где φ1 – φ2=U – разность потенциалов (напряжение) на концах участка цепи;
R – сопротивление участка;
б) для участка цепи, содержащего ЭДС, 
, (2.42)
где ε – ЭДС источника тока; R – полное сопротивление участка (сумма внешних и внутренних сопротивлений);
в) для замкнутой (полной) цепи 
, (2.43)
где r – внутреннее сопротивление цепи; R – внешнее сопротивление цепи.
20. Сопротивление R и проводимость G проводника:
(2.44)
где ρ – удельное сопротивление; σ – удельная проводимость; l – длина проводника; S – площадь поперечного сечения проводника.
21. Сопротивление системы проводников:
· при последовательном соединении 
; (2.45)
· при параллельном соединении 
, (2.46)
где Ri – сопротивление i -го проводника.
22. Работа тока:
(2.47)
Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две – для участка, не содержащего ЭДС.
23. Мощность тока:
. (2.48)
24. Закон Джоуля- Ленца:
(2.49)
