Пример 1.1. Автобус движется со скоростью 18 км/ч. С некоторого момента он начинает двигаться с ускорением a в течение 10 с, а последние 110 м проходит за одну секунду. Определить ускорение и конечную скорость автобуса.
Дано: 
=18 км/ч=5м/с,
t1=10 с,
t2=1 с,
S2=110 м.
Найти: a, 
Решение
   
S1, t1 S2, t2
|
Весь путь, проделанный автобусом, делится на два S1 и S2 (рис.1).
Рис. 1.
Запишем для двух этих участков уравнения движения:
; (1.1.1)
(1.1.2)
и законы изменения скорости:
; (1.1.3)
. (1.1.4)
Подставим (1.1.3) в (1.1.2):
. (1.1.5)
Выразим a:
. (1.1.6)
Подставим в (1.1.6) числовые данные:
.
Теперь подставим (1.1.3) в (1.1.4) и вычислим конечную скорость:
.
Ответ: ускорение автобуса a=10м/с2, конечная скорость автобуса =115м/с.
Пример 1.2. Колесо вращается с частотой 180об/мин. С некоторого момента колесо начинает вращаться равнозамедленно с угловым ускорением 3 рад/с2. Через какое время колесо остановится? Найти число оборотов колеса до остановки.
Дано: ν = 180об/мин=3об/с,
ε = 3 рад/с2.
Найти: t, n.
Решение
Запишем уравнение движения тела, совершающего равноускоренное, вращательное движение:
(1.2.1)
и закон изменения скорости
. (1.2.2)
Здесь Δφ – угол поворота тела за время t, ω0 и ω – угловая скорость тела в начальный момент времени и в момент времени t соответственно, ε – угловое ускорение.
Угол поворота Δφ связан с числом оборотов n соотношением:
. (1.2.3)
Начальную угловую скорость ω0 найдем из соотношения:
. (1.2.4)
С учетом (1.2.3) и (1.2.4), а также с учетом того, что колесо движется равнозамедленно, перепишем (1.2.1):
. (1.2.5)
Из уравнения (1.2.2) найдем время до остановки колеса, т.е. время, когда угловая скорость ω стала равна нулю:
. (1.2.6)
Рассчитаем время t:
.
Теперь подставим (1.2.6) в (1.2.5):
. (1.2.7)
Выразим из (1.2.7) число оборотов n и подставим числовые данные:
.
Ответ: колесо остановится через 6,28 с; число оборотов n=9,4 оборота.
Пример 1.3. Шар массой 2 кг, движущийся горизонтально со скоростью 
=4 м/с, столкнулся с неподвижным шаром массой 3 кг. Считая удар центральным и абсолютно неупругим, найти количество теплоты, выделившееся при ударе.
Дано: m1 = 2 кг,
m2 = 3 кг,
= 4 м/с,
= 0 м/с.
Найти: Q.
Решение
Запишем закон сохранения импульса:
. (1.3.1)
Здесь и – скорости первого и второго шаров до удара соответственно, u1 и u2 – скорости первого и второго шаров после удара соответственно. После неупругого столкновения тела движутся с одинаковой скоростью, поэтому u1 = u2 = u. Запишем проекцию уравнения (1.3.1) на направление движения шаров с учетом того, что =0 м/с:
. (1.3.2)
При неупругом ударе закон сохранения энергии не выполняется. Разность между энергией системы до удара (ЕК1) и энергией после удара (ЕК2) равна количеству теплоты, выделившемуся при ударе:
. (1.3.3)
Кинетическая энергия системы до удара:
. (1.3.4)
Кинетическая энергия системы после удара:
. (1.3.5)
Выразим из (1.3.2) u и подставим в (1.3.5):
. (1.3.6)
С учетом (1.3.4) и (1.3.6) вычислим количество теплоты Q:
.
Ответ: количество теплоты, выделившееся при ударе Q=9,6 Дж.
Пример 1.4. На барабан радиусом 0,5 м намотан шнур, к концу которого привязан груз массой 12 кг. Найти момент инерции барабана, если груз опускается с ускорением 1,81 м/с2. Барабан считать однородным цилиндром. Трением пренебречь.
Дано: R=0,5м,
m=12 кг,
a=1,81 м/с2.
| О R T α T a Y mg |
Найти: J.
Решение
Рис. 2
Запишем основной закон динамики вращательного движения:
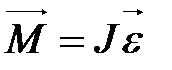. (1.4.1)
Здесь J – момент инерции цилиндра относительно оси вращения, проходящей через центр масс, ε – угловое ускорение (ускорение вращательного движения), M – момент силы, заставляющей барабан вращаться. Такой силой является сила натяжения шнура Т. Модуль момента силы равен:
. (1.4.2)
Из рис.2 видно, что α=900, поэтому:
. (1.4.3)
Угловое ускорение ε связано с линейным ускорением a соотношением:
, (1.4.4)
где R – радиус барабана.
С учетом (1.4.3) и (1.4.4) перепишем (1.4.1) в скалярном виде (вектор М и вектор ε направлены в одну сторону):
. (1.4.5)
Выразим из (1.4.5) J:
. (1.4.6)
Силу натяжения шнура Т найдем из второго закона Ньютона, записанного для поступательно движущегося груза (рис. 2):
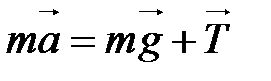. (1.4.7)
Сила натяжения шнура, вращающая барабан и сила, действующая на груз, равны по модулю и направлены в противоположные стороны. Проекция уравнения (1.4.7) на ось OY имеет вид:
. (1.4.8)
Выразим из (1.4.8) Т и подставим полученное выражение в (1.4.6):
. (1.4.9)
Проверим размерность:
.
Подставим в (1.4.9) числовые данные:
.
Ответ: момент инерции барабана J=12 м2кг.
Пример 1.5. Шар массой 0,25 кг и радиусом 3 см катится без скольжения по горизонтальной плоскости с частотой вращения 4 об/с. Найти кинетическую энергию шара.
Дано: m=0,25 кг,
R=3 см=3∙10-2 м,
ν= 4 об/с.
Найти: EК.
Решение
Кинетическая энергия шара, который катится по горизонтальной плоскости без скольжения, складывается из энергии поступательного и вращательного движения:
, (1.5.1)
где m – масса шара,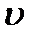 
– линейная скорость (скорость поступательного движения), J – момент инерции шара относительно оси вращения, проходящей через центр масс, ω – угловая скорость (скорость вращательного движения).
Известно, что для шара радиусом R
. (1.5.2)
Угловая скорость ω связана с линейной скоростью 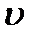соотношением:
, (1.5.3)
а с линейной частотой ν соотношением
. (1.5.4)
Подставим (1.5.2), (1.5.3) и (1.5.4) в (1.5.1) и сделаем необходимые преобразования:
. (1.5.5)
Подставим в (1.5.5) числовые данные:
.
Ответ: кинетическая энергия шара ЕК=0,1 Дж.
Задачи по теме №1
1. Автомобиль проходит последовательно два одинаковых участка пути, каждый по 10 м с постоянным ускорением, причем первый участок пути пройден автомобилем за 1 с, а второй – за 2 с. С каким ускорением движется автомобиль и какова его скорость в начале первого участка?
2. При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найти тормозной путь.
3. Зависимость скорости материальной точки от времени имеет вид: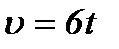 
.Материальная точка движется прямолинейно. Каков путь, пройденный точкой за 4 с?
4. Определить путь, проходимый частицей, которая движется по прямолинейной траектории в течение 10 с, если ее скорость изменяется по закону v = 30 + 2t. В момент времени t0 =0, S =0.
5. Рядом с поездом на одной линии с передними буферами паровоза стоит человек. В тот момент, когда поезд начал двигаться с ускорением 0,1 м/с2, человек начал идти в том же направлении со скоростью 1,5 м/с. Через какое время поезд догонит человека? Определить скорость поезда в этот момент и путь, пройденный за это время человеком.
6. Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через две секунды после первой. Первая точка двигалась с начальной скоростью 1 м/с и ускорением 2 м/с2, вторая – с начальной скоростью 10 м/с и ускорением 1 м/с2. Через сколько времени и на каком расстоянии от исходного положения вторая точка догонит первую?
7. Пожарный поезд прошел расстояние 17 км между двумя станциями со средней скоростью 60 км/ч. При этом на разгон в начале движения и торможения перед остановкой ушло в общей сложность 4 мин, а остальное время поезд двигался с постоянной скоростью. Чему равна эта скорость?
8. Время отправления электрички по расписанию 12.00. На ваших часах 12.00, но мимо вас уже начинает проезжать предпоследний вагон, который движется мимо вас в течение 10 с. Последний вагон проходит мимо вас в течение 8 с. Электричка отправилась вовремя и движется равноускоренно. На какое время отстают ваши часы?
9. Лыжник съехал с горы длиной 40 м за 10 с, после чего он проехал по горизонтальной площадке до остановки 20 м. Считая движение с горы равноускоренным без начальной скорости, а по горизонтальной площадке равнозамедленным, найти скорость лыжника в конце горы и среднюю скорость на всем пути.
10. При равноускоренном движении мотоциклист за первые 5 с прошел путь в 45 м, а в следующие 5 с – путь в 95 м. Найти начальную и среднюю скорости мотоциклиста.
11. Велосипедист начал свое движение из состояния покоя и в течение первых 4 с двигался с ускорением 1 м/с2, затем в течение 0,1 мин он двигался равномерно и последние 20 м – равнозамедленно до остановки. Найти среднюю скорость за все время движения.
12. С вертолета, находящегося на высоте 1960 м, сброшен гуманитарный груз. Через какое время груз достигнет земли, если вертолет: 1) неподвижен; 2) поднимается со скоростью 19,6 м/с; 3) опускается со скоростью 19,6 м/с.
13. Вертикально вверх с начальной скоростью 20 м/с брошен камень. Через 1 с после этого брошен вертикально вверх другой камень с такой же скоростью. На какой высоте встретятся камни?
14. С балкона бросили мячик вертикально вверх с начальной скоростью 5 м/с. Через 2 с мячик упал на землю. Определить высоту балкона над землей и скорость мячика в момент удара о землю.
15. Автомобиль спасательной службы движется по шоссе со скоростью 120 км/ч, а при буксировке аварийного автомобиля – со скоростью всего 30 км/ч. Чему равна его средняя скорость, если он едет половину пути один, а затем буксирует неисправный автомобиль?
16. Камень, брошенный со скоростью 12м/с под углом 450 к горизонту, упал на землю на некотором расстоянии от места бросания. С какой высоты надо бросить камень в горизонтальном направлении, чтобы при той же начальной скорости он упал на то же место?
17. Снаряд вылетает из ствола орудия, установленного на высоте 122,5 м, со скоростью 400 м/с в горизонтальном направлении. Определить время полета снаряда. Поразит ли снаряд одну из целей, расположенных на расстоянии 2 км и 5,8 км от орудия (по горизонтали) в направлении полета снаряда? Сопротивлением воздуха пренебречь.
18. Камень брошен с вышки со скоростью 29.4м/с в горизонтальном направлении. Найти радиус кривизны траектории камня в точке, где он будет через 4с после начала движения.
19. Камень брошен горизонтально. Через 3с его скорость оказалась направленной под углом 450 к горизонту. Определить начальную скорость камня.
20. Под углом 600 к горизонту брошено тело с начальной скоростью 20 м/с. Через какой промежуток времени оно будет двигаться под углом 450 к горизонту.
21. Дальность полета тела, брошенного горизонтально со скоростью 4,9 м/с, равна высоте бросания. Под каким углом к горизонту направлена скорость тела в момент его падения на землю?
22. Мяч брошен со скоростью υ0 под углом α к горизонту. Найти υ0 и α, если максимальная высота подъема мяча 3м, а радиус кривизны траектории мяча в этой точке 3м.
23. Под каким углом к горизонту надо бросить тело, чтобы высота подъема была в два раза больше дальности полета?
24. Камень брошен с вышки в горизонтальном направлении с начальной скоростью 30 м/с. Определить скорость, тангенциальное и нормальное ускорения камня в конце второй секунды после начала движения.
25. Камень брошен с вышки в горизонтальном направлении. Через промежуток времени 2 с камень упал на землю на расстоянии 40 м от основания вышки. Определить начальную и конечную скорости камня.
26. Камень, брошенный горизонтально на высоте 6 м, упал на землю на расстоянии 10 м от точки бросания. Найдите начальную скорость камня, нормальное и тангенциальное ускорение камня через время 0,2 с после начала движения.
27. Через какое время вектор скорости тела, брошенного под углом 60° к горизонту с начальной скоростью 20 м/с, будет составлять с горизонтом угол 30°? Сопротивление воздуха не учитывать.
28. Артиллерийское орудие установлено на горе высотой 75,5 м. Снаряд вылетает из ствола со скоростью 500 м/с под углом 30 к горизонту. Определить дальность полета снаряда и скорость полета в момент падения. Сопротивление воздуха не учитывать.
29. С башни высотой 30 м в горизонтальном направлении брошено тело с начальной скоростью 10 м/с. Определить скорость тела в момент падения на землю и угол, который образует эта скорость с горизонтом в точке его падения.
30. Миномет, установленный на крыше здания высотой 60 м, стреляет под углом 30° к горизонту и поражает цель, удаленную на расстояние 7500 м (по горизонтали). Определить начальную скорость мины и продолжительность ее полета. Сопротивление воздуха не учитывать.
31. Точка движется по окружности радиуса 20 см с постоянным тангенциальным ускорением 5 м/с2. Через какое время после начала движения нормальное ускорение точки будет равно тангенциальному?
32. Зависимость пройденного телом пути по окружности радиусом 3 м задается уравнением S = At 2 + Bt (A = 0,4 м/с2, В = 0,1 м/с). Определить нормальное, тангенциальное и полное ускорение тела через 1 c после начала движения.
33. Трамвай, начав двигаться равноускоренно по закругленному участку пути и пройдя 100 м, развил скорость 36 км/ч. Каковы тангенциальное и нормальное ускорения трамвая в конце десятой секунды после начала движения?
34. Поезд движется равнозамедленно по закруглению радиуса R и, пройдя путь S, приобретает скорость vk. Его начальная скорость vH. Найти время движения и полное ускорение в начале и в конце пути.
35. По дуге окружности радиусом 10 м движется точка. В некоторый момент времени нормальное ускорение точки 4,9 м/с2; в этот момент векторы полного и нормального ускорений образуют угол 60. Найти скорость и тангенциальное ускорение точки.
36. С какой угловой скоростью вращается колесо, если линейная скорость точек его обода равна 0,5 м/с, а линейная скорость точек, находящихся на 4 см ближе к оси вращения, равна 0,3 м/с?
37. Ось с двумя дисками, расположенными на расстоянии 0,5 м друг от друга вращается с частотой 1600 об/мин. Пуля, летящая вдоль оси, пробивает оба диска; при этом отверстие от пули во втором диске смещено относительно отверстия в первом диске на угол 120. Найти скорость пули.
38. Маховик начал вращаться равноускоренно и за промежуток времени 10 с достиг частоты вращения 300 об/мин. Определить угловое ускорение маховика и число оборотов, которое он сделал за это время.
39. Диск вращается с угловым ускорением -2 рад/с2. Сколько оборотов сделает диск при изменении частоты вращения от 240 об/мин до 90 об/мин? Найти время, в течении которого это произойдет.
40. Материальная точка начинает двигаться по окружности радиусом 12,5 см с постоянным тангенциальным ускорением 0,5 см/с2. Определить момент времени, при котором вектор ускорения образует с вектором скорости угол 45°
41. Найти радиус вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 2,5 раза больше линейной скорости точки, лежащей на расстоянии 5 см ближе к оси колеса.
42. Ось с двумя дисками, расположенными на расстоянии 0,5 м друг от друга вращается с частотой 1600 об/мин. Пуля, летящая вдоль оси, пробивает оба диска; при этом отверстие от пули во втором диске смещено относительно отверстия в первом диске на угол 12°. Найти скорость пули.
43. Колесо начинает вращаться из состояния покоя и через 1,5 с достигает угловой скорости 20 рад/с. На какой угол оно повернулось за указанное время?
44. Колесо вращается с постоянным угловым ускорением 3 рад/с2. Определить радиус колеса, если через 1 с после начала движения полное ускорение колеса 7,5 м/с2.
45. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.
46. В шахту равноускоренно опускается бадья массой 280 кг. В первые 10 с она проходит 35 м. Найти силу натяжения каната, на котором висит бадья.
47. Вагон массой 20 т движется с начальной скоростью 54 км/ч. Определить среднюю силу, действующую на вагон, если известно, что вагон останавливается в течении 1 мин 40 с.
48. Автомобиль массой 1020 кг останавливается при торможении за 5 с, пройдя при этом равнозамедленно расстояние 25 м. Найти начальную скорость автомобиля и силу торможения.
49. На автомобиль массой 1 т во время движения действует сила трения, равная 0,1 его силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью в гору с уклоном 1 м на каждые 25 м пути.
50. По наклонной плоскости высотой 0,5 м и длиной склона 1 м скользит тело массой 3 кг. Тело приходит к основанию наклонной плоскости со скоростью 2,45 м/с. Найти коэффициент трения тела о плоскость/ Начальная скорость равна нулю.
51. Наклонная плоскость, образующая угол 250 с плоскостью горизонта, имеет длину 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время 2 с. Определить коэффициент трения тела о плоскость.
52. Камень, пущенный по поверхности льда со скоростью 3 м/с, прошел до остановки расстояние 20,4 м. Найти коэффициент трения камня о лед.
53. Тело скользит по наклонной плоскости, образующей с горизонтом угол 450. Пройдя путь 36,4 см тело приобретает скорость 2 м/с. Найти коэффициент трения тела о плоскость.
54. Тело скользит с наклонной плоскости высотой h и углом наклона a к горизонту и движется далее по горизонтальному участку. Принимая коэффициент трения на всем пути постоянным и равным μ, определить расстояние S, пройденное телом на горизонтальном участке, до полной остановки.
55. Стальная проволока выдерживает груз до 5000 Н. С каким наибольшем ускорением можно поднимать груз в 4500 Н, подвешенный на этой проволоке, чтобы она не разорвалась?
56. К нити подвешен груз массой 500 г. Определить силу натяжения нити, если нить с грузом: 1)поднимается с ускорением 2 м/c2; 2) опускается с ускорением 2 м/с2.
57. При разборе завала используется подъемный кран. Трос крана выдерживает силу натяжения 4000 Н. С каким наибольшим ускорением можно поднимать обломок стены массой 400 кг, чтобы трос при этом не разорвался?
58. Масса лифта с пассажирами равна 800 кг. Найти, с каким ускорением и в каком направлении движется лифт, если известно, что натяжение троса поддерживающего лифт, равно 11760 Н.
59. С каким ускорением нужно поднимать гирю, чтобы ее вес увеличился вдвое? С каким ускорением нужно ее опускать, чтобы вес уменьшился вдвое?
60. На столе стоит тележка массой 4 кг. К тележке привязан один конец шнура, перекинутого через блок. С каким ускорением будет двигаться тележка, если к другому концу шнура привязать гирю массой 1 кг?
61. Молекула массой 4,65×10-26 кг, летящая нормально к стенке сосуда со скоростью 600 м/с, ударяется о стенку и упруго отталкивается от нее без потери скорости. Найти импульс силы, полученный стенкой за время удара.
62. Молекула массой 4,65×10-26 кг, летящая со скоростью 600 м/с, ударяется о стенку сосуда под углом 600 к нормали и под таким же углом упруго отталкивается от нее без потери скорости. Найти импульс силы, полученный стенкой за время удара.
63. Мяч массы 150 г ударяется о гладкую стенку под углом 300 к ней и отскакивает без потери скорости. Найти среднюю силу, действующую на мяч со стороны стенки, если скорость мяча 10 м/с, а продолжительность удара 0,1 с.
64. Два шара массами 9 кг и 12 кг подвешены на нитях длиной 1,5 м. Первоначально шары соприкасаются между собой, затем меньший шар отклонили на угол 300 и отпустили. Считая удар неупругим, определить высоту на которую поднимутся оба шара после удара.
65. Тело массой 2 кг движется навстречу второму телу массой 1,5 кг и абсолютно неупруго соударяется с ним. Скорости тел непосредственно перед ударом были 1 м/с и 2 м/с. Какое время будут двигаться эти тела после удара, если коэффициент трения 0,05?
66. Шар массой 2 кг, движущийся горизонтально со скоростью 4 м/с, столкнулся с неподвижным шаром массой 3 кг. Считая удар центральным и абсолютно неупругим, найти количество теплоты, выделившееся при ударе.
67. Лодка массой 150 кг и длиной2,8 м стоит неподвижно в стоячей воде. Рыбак массой 90 кг в лодке переходит с носа на корму. Пренебрегая сопротивлением воды, определить, на какое расстояние s при этом сдвинется лодка.
68. Тело массой 2 кг движется со скоростью 3 м/с и нагоняет второе тело массой 3 кг, движущееся со скоростью 1 м/с. Каково должно быть соотношение между массами тел, чтобы при упругом ударе первое тело после удара остановилось?
69. Снаряд массой 20 кг, летевший со скоростью, направленной под углом 300 к горизонту, попадает в платформу с песком массой 104 кг и застревает в песке. С какой скоростью летел снаряд, если платформа начинает двигаться со скоростью 1 м/с?
70. Камень массой 400 г бросили со скоростью 20 м/с в горизонтальном направлении с башни, высота которой 50 м. Найти потенциальную и кинетическую энергии камня через 2 с после начала его движения.
71. Автомобиль массой 2 т затормозил и остановился, пройдя путь 50 м. найти работу силы трения, если дорога горизонтальна и коэффициент трения равен 0,4.
72. Гиря, положенная на верхний конец спиральной пружины, сжимает ее на 2 мм. На сколько сожмет пружину та же гиря, упавшая на конец пружины с высоты 5 см?
73. Молот массой 70 кг падает с высоты 5 м и ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе с изделием 1330 кг. Считая удар абсолютно неупругим, определить энергию, расходуемую на деформацию изделия.
74. Автомобиль массой 2 т движется в гору. Уклон горы равен 4 м на каждые 100 м пути. Коэффициент трения равен 8%. Найти работу, совершенную двигателем автомобиля на пути 3 км.
75. Найти, какую мощность развивает двигатель автомобиля массой 1 т, если известно, что автомобиль едет с постоянной скоростью 36 км/ч по горизонтальной дороге.
76. Определить момент силы, который необходимо приложить к однородному диску, вращающемуся с частотой 12 с-1, чтобы он остановился через 8 с. Диаметр диска 30 см, масса диска 6 кг.
77. К ободу колеса радиусом 0,5 м и массой 50 кг приложена касательная сила 98,1 Н. Найти угловое ускорение колеса. Через какое время после начала действия силы колесо будет иметь частоту вращения 100 об/с? Колесо считать однородным диском. Трением пренебречь.
78. Маховик, момент инерции которого 63,6 кг⋅м2, вращается с угловой скоростью 31,4 рад/с. Найти момент сил торможения, под действием которого маховик остановится через 20 с. Маховик считать однородным диском.
79. На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. Двигаясь равноускоренно, грузик за время 3 c опустился на 1,5 м. Определите угловое ускорение цилиндра, если его радиус 4 см.
80. На однородный сплошной цилиндрический вал радиусом 50 см намотана легкая нить, к концу которой прикреплен груз массой 6,4 кг. Груз, опускается с ускорением 2 м/с2. Определить момент инерции вала и массу вала.
81. На однородный сплошной цилиндрический вал радиусом 5 см и массой 10 кг намотана легкая нить, к концу которой прикреплен груз 1 кг. Определить силу натяжения нити.
82. На барабан радиусом 0,5 м намотан шнур, к концу которого привязан груз 10 кг. Найти момент инерции барабана, если известно, что груз опускается с ускорением 2,04 м/с2.
83. К ободу однородного сплошного диска массой 10 кг, насаженного на ось, приложена постоянная касательная сила 30 Н. Определить кинетическую энергию диска через время 4 с после начала действия силы.
84. Маховик вращается с постоянной скоростью, соответствующей частоте 10 об/с; его кинетическая энергия 7,85 кДж. За сколько времени вращающий момент 50 Н·м, приложенный к этому маховику, увеличит угловую скорость в два раза?
85. Определить тормозящий момент, которым можно остановить за 20 с маховое колесо массой 50 кг и радиусом 0,30 м, вращающееся с частотой 20 об/с. Массу маховика считать распределённой по ободу. Чему равна работа, совершаемая тормозящим моментом?
86. По горизонтальной плоской поверхности катится диск со скоростью 8 м/с. Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь в 18 м.
87. Сплошной цилиндр массой 10 кг катится без скольжения с постоянной скоростью 10 м/с. Определить кинетическую энергию цилиндра и время до его остановки, если на него действует сила трения 50 Н.
88. Сплошной шар скатывается без проскальзывания по наклонной плоскости, длина которой 10 м и угол наклона 300. Определить скорость шара в конце наклонной плоскости. Трение шара о плоскость не учитывать.
89. Полый тонкостенный цилиндр массой 2 кг катится по горизонтальной поверхности со скоростью 20 м/с. Определить силу, которую необходимо приложить к цилиндру, чтобы остановить его на пути 1,6 м.
90. Какой путь пройдет катящийся без скольжения диск, поднимаясь вверх по наклонной плоскости с углом наклона 300, если ему сообщена начальная скорость 7,0 м/с, параллельная наклонной плоскости.
КОНТРОЛЬНАЯ РАБОТА №2
