Кремер Н.Ш.
Теория вероятностей
Примеры решений типовых задач и задания для студентов
ГЛАВА
Основные понятия и теоремы теории вероятностей
В главе рассматриваются:
- классификация событий;
- классическое, статистическое и геометрическое определения вероятности;
- непосредственное вычисление вероятностей;
- действия над событиями;
- теоремы сложения и умножения вероятностей;
- формула Байеса.
Типовые задачи
Пример 1.1
Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,9; третий – 0,8. Найти вероятность того, что студентом будут сданы:
а) только 2-й экзамен;
б) только один экзамен;
в) три экзамена;
г) по крайней мере два экзамена;
д) хотя бы один экзамен.
Решение
а) Обозначим события: Ai – студент сдаст i -йэкзамен (i = 1, 2, 3);
В – студент сдаст только 2-й экзамен из трех.
Очевидно, что В =  , т.е. совместное осуществление трех событий, состоящих в том, что студент сдаст 2-й экзамен и не сдаст 1-й и 3-й экзамены. Учитывая, что события A1, А2, А3 независимы, получим
, т.е. совместное осуществление трех событий, состоящих в том, что студент сдаст 2-й экзамен и не сдаст 1-й и 3-й экзамены. Учитывая, что события A1, А2, А3 независимы, получим

б) Пусть событие С – студент сдаст один экзамен из трех. Очевидно, событие С произойдет, если студент сдаст только 1-й экзамен из трех, или только 2-й, или только 3-й, т.е.

в) Пусть событие D – студент сдаст все три экзамена, т.е. D =
A1
A2
A3. Тогда

г) Пусть событие Е – студент сдаст по крайней мере два экзамена (иначе: «хотя бы два» экзамена или «не менее двух» экзаменов). Очевидно, что событие Е означает сдачу любых двух экзаменов из трех либо всех трех экзаменов, т.е.
 и
и

д) Пусть событие F – студент сдал хотя бы один экзамен (иначе: «не менее одного» экзамена). Очевидно, событие F представляет сумму событий С (включающего три варианта) и Е (четыре варианта), т.е. F = А1 + А2 + А3 = С + Е (семь вариантов). Однако проще найти вероятность события F, если перейти к противоположному событию, включающему всего один вариант – F =  , т.е. применить формулу (1.27).
, т.е. применить формулу (1.27).
Итак,

т.е. сдача хотя бы одного экзамена из трех является событием практически достоверным.
Пример 1.2
Причиной разрыва электрической цепи служит выход из строя элемента К1 или одновременный выход из строя двух элементов – К2 и К3. Элементы могут выйти из строя независимо друг от друга с вероятностями, равными соответственно 0,1; 0,2; 0,3. Какова вероятность разрыва электрической цепи?
Решение
Обозначим события: Ai - выход из строя элемента Ki (
i - 1, 2, 3…);
B – разрыв электрической цепи.
Очевидно, по условию событие B произойдет, если произойдет либо событие А1, либо A2A3,т.е. B = А1 + А2А3. Теперь, по формуле (1.25)



(при использовании теоремы умножения учли независимость событий A1,
A2 и А3).
Пример 1.3
Производительности трех станков, обрабатывающих одинаковые детали, относятся как 1:3:6. Из нерассортированной партии обработанных деталей взяты наудачу две. Какова вероятность того, что: а) одна из них обработана на 3-м станке;
б) обе обработаны на одном станке?
Решение
а) Обозначим события: Ai – деталь обработана на i -мстанке (i = 1, 2, 3);
В – одна из двух взятых деталей обработана на 3-м станке.
По условию 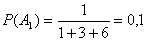 ,
,  ,
,  .
.
Очевидно, что B=
A1
A3+
A2
A3+
A3
A1+
A3
A2 (при этом надо учесть, что либо первая деталь обработана на 3-м станке, либо вторая). По теоремам сложения и умножения (для независимых событий)


б) Пусть событие С – обе отобранные детали обработаны на одном станке. Тогда
C=
A1
A1+
A2
A2+
A3
A3 и P(C) = 0,1*0,1 + 0,3*0,3 + 0,6*0,6 = 0,46.
Пример 1.4
Экзаменационный билет для письменного экзамена состоит из 10 вопросов – по 2 вопроса из 20 по каждой из пяти тем, представленных в билете. По каждой теме студент подготовил лишь половину всех вопросов. Какова вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на один вопрос по каждой из пяти тем в билете?
Решение
Обозначим события: А1, А2 – студент подготовил 1-й, 2-й вопросы билета по каждой теме;
Bi – студент подготовил хотя бы один вопрос билета из двух по i -й теме (i = 1, 2,..., 5);
С – студент сдал экзамен.
В силу условия С = В1В2В3В4
B5. Полагая ответы студента по разным темам независимыми, по теореме умножения вероятностей (1.24)

Так как вероятности Р(В
i) (i =1,2,..., 5) равны, то P(C)= (Р(В
i))5. Вероятность Р(В
i) можно найти по формуле (1.27) (или (1.25)):

Теперь P(C) = 0,7635 = 0,259
Пример 1.5
При включении зажигания двигатель начнет работать с вероятностью 0,6. Найти вероятность того, что:
а) двигатель начнет работать при третьем включении зажигания;
б) для запуска двигателя придется включать зажигание не более трех раз.
Решение
а) Обозначим события: А – двигатель начнет работать при каждом включении зажигания;
В – то же при третьем включении зажигания.
Очевидно, что В=  и Р(В) =
и Р(В) =  = 0,4*0,4*0,6 = 0,096.
= 0,4*0,4*0,6 = 0,096.
б) Пусть событие С – для запуска двигателя придется включать зажигание не более трех раз. Очевидно, событие С наступит, если двигатель начнет работать при 1-м включении, или при 2-м, или при 3-м включении, т.е. С = А + АА + А АА. Следовательно,

Пример 1.6
Среди билетов денежно-вещевой лотереи половина выигрышных. Сколько лотерейных билетов нужно купить, чтобы с вероятностью, не меньшей 0,999, быть уверенным в выигрыше хотя бы по одному билету?
Решение
Пусть вероятность события A i – выигрыша по i -мy билету равна р, т.е. P(
Ai) = р. Тогда вероятность выигрыша хотя бы по одному из п приобретенных билетов, т.е. вероятность суммы независимых событий A1,
A2,...,
Ai,...,
An определится по формуле (1.29):
P(A1+A2+…+An) = 1-(1-p)n
По условию 1-(1-p)n ≥ R, где R = 0,999, откуда
(1 - p)n ≤ 1 – R
Логарифмируя обе части неравенства, имеем
n lg(1 - p) ≤ lg(1 - R)
Учитывая, что lg(1 - p) – величина отрицательная, получим
 (1.30)
(1.30)
По условию р = 0,5, R = 0,999. По формуле (1.30)
 ,
,
т.е. n ≥ 10 и необходимо купить не менее 10 лотерейных билетов.
(Задачу можно решить, не прибегая к логарифмированию, путем подбора целого числа n, при котором выполняется неравенство (1 - p)n ≤ 1 – R, т.е. в данном случае  ; так, еще при n = 9
; так, еще при n = 9  =
=  , а уже при n = 10
, а уже при n = 10  =
=  , т.е. n ≥ 10).
, т.е. n ≥ 10).
Пример 1.7
Два игрока поочередно бросают игральную кость. Выигрывает тот, у которого первым выпадет «6 очков». Какова вероятность выигрыша для игрока, бросающего игральную кость первым? Вторым?
Решение
Обозначим события: Ai – выпадение 6 очков при i- мбросании игральной кости (i =1,2,...);
В – выигрыш игры игроком, бросающим игральную кость первым.
Имеем P(Ai) = 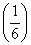 ,
,  при любом i.
при любом i.
Событие В можно представить в виде суммы вариантов:

Поэтому
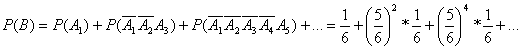
По формуле суммы геометрического ряда с первым членом a = 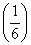 и знаменателем q =
и знаменателем q = 

Вероятность  выигрыша игры игроком, бросающим игральную кость вторым, равна
выигрыша игры игроком, бросающим игральную кость вторым, равна
 ,
,
т.е. существенно меньше, чем игроком, бросающим игральную кость первым.
Пример 1.8
Вероятность попадания в мишень при каждом выстреле для 1-го стрелка равна 0,7, а для 2-го – 0,8. Оба они делают по одному выстрелу по мишени, а затем каждый из стрелков стреляет еще раз, если при первом сделанном им выстреле он промахнулся. Найти вероятность того, что в мишени ровно 2 пробоины.
Решение
Пусть события: Ai,
Bi – попадание в цель соответственно 1-м 2-м стрелком при i -м выстреле (i =1,2);
С – в мишени ровно 2 пробоины.
Событие С произойдет, если:
• у каждого стрелка по одному попаданию с первого раза;
• у 1-го стрелка – попадание (при одном выстреле), у 2-го стрелка промах и попадание;
• у 1-го стрелка – промах и попадание, у 2-го стрелка – попадание (при одном выстреле);
• у каждого стрелка – промах и попадание после двух выстрелов.
Итак

Используя теоремы сложения для несовместных и умножения для независимых событий, получим


Задания
1.1. Слово составлено из карточек, на каждой из которых написана одна буква. Карточки смешивают и вынимают без возврата по одной. Найти вероятность того, что карточки с буквами вынимаются в порядке следования букв заданного слова:
а) «событие»;
б) «статистика».
1.2. Пятитомное собрание сочинений расположено на полке в случайном порядке. Какова вероятность того, что книги стоят слева направо в порядке нумерации томов (от 1 до 5)?
1.3. Среди 25 студентов, из которых 15 девушек, разыгрываются четыре билета, причем каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билета окажутся:
а) четыре девушки;
б) четыре юноши;
в) три юноши и одна девушка?
1.4. Из 20 сбербанков 10 расположены за чертой города. Для обследования случайным образом отобрано 5 сбербанков. Какова вероятность того, что среди отобранных окажется в черте города:
а) 3 сбербанка;
б) хотя бы один?
1.5. Из ящика, содержащего 5 пар обуви, из которых три пары мужской, а две пары женской обуви, перекладывают наудачу 2 пары обуви в другой ящик, содержащий одинаковое количество пар женской и мужской обуви. Какова вероятность того, что во втором ящике после этого окажется одинаковое количество пар мужской и женской обуви?
1.6. В магазине имеются 30 телевизоров, причем 20 из них импортных. Найти вероятность того, что среди 5 проданных в течение дня телевизоров окажется не менее 3 импортных телевизоров, предполагая, что вероятности покупки телевизоров разных марок одинаковы.
1.7. Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность того, что в нем все цифры:
а) различные;
б) одинаковые;
в) нечетные?
Известно, что номер телефона не начинается с цифры ноль.
1.8. Для проведения соревнования 16 волейбольных команд разбиты по жребию на две подгруппы (по восемь команд в каждой). Найти вероятность того, что две наиболее сильные команды окажутся:
а) в разных подгруппах;
б) в одной подгруппе.
1.9. Студент знает 20 из 25 вопросов программы. Зачет считается сданным, если студент ответит не менее чем на 3 из 4 поставленных в билете вопросов. Взглянув на первый вопрос билета, студент обнаружил, что он его знает. Какова вероятность того, что студент:
а) сдаст зачет;
б) не сдаст зачет?
1.10. У сборщика имеются 10 деталей, мало отличающихся друг от друга, из них четыре – первого, по две – второго, третьего и четвертого видов. Какова вероятность того, что среди шести взятых одновременно деталей три окажутся первого вида, два – второго и одна – третьего?
1.11. Найти вероятность того, что из 10 книг, расположенных в случайном порядке, 3 определенные книги окажутся рядом.
1.12. В старинной игре в кости необходимо было для выигрыша получить при бросании трех игральных костей сумму очков, превосходящую 10. Найти вероятности:
а) выпадения 11 очков;
б) выигрыша.
1.13. На фирме работают 8 аудиторов, из которых 3 – высокой квалификации, и 5 программистов, из которых 2 – высокой квалификации. В командировку надо отправить группу из 3 аудиторов и 2 программистов. Какова вероятность того, что в этой группе окажется по крайней мере 1 аудитор высокой квалификации и хотя бы 1 программист высокой квалификации, если каждый специалист имеет равные возможности поехать в командировку?
1.14. Два лица условились встретиться в определенном месте между 18 и 19 ч и договорились, что пришедший первым ждет другого в течение 15 мин., после чего уходит. Найти вероятность их встречи, если приход каждого в течение указанного часа может произойти в любое время и моменты прихода независимы.
1.15. Какова вероятность того, что наудачу брошенная в круг точка окажется внутри вписанного в него квадрата?
1.16. При приеме партии изделий подвергается проверке половина изделий. Условие приемки – наличие брака в выборке менее 2%. Вычислить вероятность того, что партия из 100 изделий, содержащая 5% брака, будет принята.
1.17. По результатам проверки контрольных работ оказалось, что в первой группе получили положительную оценку 20 студентов из 30, а во второй – 15 из 25. Найти вероятность того, что наудачу выбранная работа, имеющая положительную оценку, написана студентом первой группы.
1.18. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе отделение – 0,9 и в третье – 0,8. Найти вероятность следующих событий:
а) только одно отделение получит газеты вовремя;
б) хотя бы одно отделение получит газеты с опозданием.
1.19. Прибор, работающий в течение времени t, состоит из трех узлов, каждый из которых независимо от других может за это время выйти из строя. Неисправность хотя бы одного узла выводит прибор из строя целиком. Вероятность безотказной работы в течение времени t первого узла равна 0,9, второго – 0,95, третьего – 0,8. Найти вероятность того, что в течение времени t прибор выйдет из строя.
1.20. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором и третьем справочниках, равна соответственно 0,6, 0,7 и 0,8. Найти вероятность того, что эта формула содержится не менее, чем в двух справочниках.
1.21. Произведено три выстрела по цели из орудия. Вероятность попадания при первом выстреле равна 0,75; при втором – 0,8; при третьем – 0,9. Определить вероятность того, что будет:
а) три попадания;
б) хотя бы одно попадание.
1.22. Вероятность своевременного выполнения студентом контрольной работы по каждой из трех дисциплин равна соответственно 0,6, 0,5 и 0,8. Найти вероятность своевременного выполнения контрольной работы студентом:
а) по двум дисциплинам;
б) хотя бы по двум дисциплинам.
1.23. Мастер обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания рабочего, равна 0,3, второй – 0,6, третий – 0,4 и четвертый – 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера.
1.24. Контролер ОТК, проверив качество сшитых 20 пальто, установил, что 16 из них первого сорта, а остальные – второго. Найти вероятность того, что среди взятых наудачу из этой партии трех пальто одно будет второго сорта.
1.25. Среди 20 поступающих в ремонт часов 8 нуждаются в общей чистке механизма. Какова вероятность того, что среди взятых одновременно наудачу 3 часов по крайней мере двое нуждаются в общей чистке механизма?
1.26. Среди 15 лампочек 4 стандартные. Одновременно берут наудачу 2 лампочки. Найти вероятность того, что хотя бы одна из них нестандартная.
1.27. В коробке смешаны электролампы одинакового размера и формы: по 100 Вт – 7 штук, по 75 Вт – 13 штук. Вынуты наудачу 3 лампы. Какова вероятность того, что:
а) они одинаковой мощности;
б) хотя бы две из них по 100 Вт?
1.28. В коробке 10 красных, 3 синих и 7 желтых карандашей. Наудачу вынимают 3 карандаша. Какова вероятность того, что они все:
а) разных цветов;
б) одного цвета?
1.29. Брак в продукции завода вследствие дефекта А составляет 4%, а вследствие дефекта В – 3,5%. Годная продукция завода составляет 95%. Найти вероятность того что:
а) среди продукции, не обладающей дефектом А, встретится дефект В;
б) среди забракованной по признаку А продукции встретится дефект В.
1.30. Пакеты акций, имеющихся на рынке ценных бумаг, могут дать доход владельцу с вероятностью 0,5 (для каждого пакета). Сколько пакетов акций различных фирм нужно приобрести, чтобы с вероятностью, не меньшей 0,96875, можно было ожидать доход хотя бы по одному пакету акций?
1.31. Сколько раз нужно провести испытание, чтобы с вероятностью, не меньшей Р, можно было утверждать, что по крайней мере один раз произойдет событие, вероятность которого в каждом испытании равна P? Дать ответ при P = 0,4 и Р = 0,8704.
1.32. На полке стоят 10 книг, среди которых 3 книги по теории вероятностей. Наудачу берутся три книги. Какова вероятность, что среди отобранных хотя бы одна книга по теории вероятностей?
1.33. На связке 5 ключей. К замку подходит только один ключ. Найти вероятность того, что потребуется не более двух попыток открыть замок, если опробованный ключ в дальнейших испытаниях не участвует.
1.34. В магазине продаются 10 телевизоров, 3 из них имеют дефекты. Какова вероятность того, что посетитель купит телевизор, если для выбора телевизора без дефектов понадобится не более трех попыток?
1.35. Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,2, второй – 0,3, третий – 0,4. События, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент услышит вызов радиста.
1.36. Страховая компания разделяет застрахованных по классам риска: I класс – малый риск, II класс – средний, III класс – большой риск. Среди этих клиентов 50% – первого класса риска, 30% – второго и 20% – третьего. Вероятность необходимости выплачивать страховое вознаграждение для первого класса риска равна 0,01, второго – 0,03, третьего – 0,08. Какова вероятность того, что:
а) застрахованный получит денежное вознаграждение за период страхования;
б) получивший денежное вознаграждение застрахованный относится к группе малого риска?
1.37. В данный район изделия поставляются тремя фирмами в соотношении 5:8:7. Среди продукции первой фирмы стандартные изделия составляют 90%, второй – 85%, третьей – 75%. Найти вероятность того, что:
а) приобретенное изделие окажется нестандартным;
б) приобретенное изделие оказалось стандартным.
Какова вероятность того, что оно изготовлено третьей фирмой?
1.38. Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,6, а для второго – 0,3. В мишени оказалась одна пробоина. Найти вероятность того, что она принадлежит первому стрелку.
1.39. Вся продукция цеха проверяется двумя контролерами, причем первый контролер проверяет 55% изделий, а второй – остальные. Вероятность того, что первый контролер пропустит нестандартное изделие, равна 0,01, второй – 0,02. Взятое наудачу изделие, маркированное как стандартное, оказалось нестандартным. Найти вероятность того, что это изделие проверялось вторым контролером.
1.40. Вероятность изготовления изделия с браком на данном предприятии равна 0,04. Перед выпуском изделие подвергается упрощенной проверке, которая в случае бездефектного изделия пропускает его с вероятностью 0,96, а в случае изделия с дефектом – с вероятностью 0,05. Определить:
а) какая часть изготовленных изделий выходит с предприятия;
б) какова вероятность того, что изделие, выдержавшее упрощенную проверку, бракованное?
1.41. В одной урне 5 белых и 6 черных шаров, а в другой – 4 белых и 8 черных шаров. Из первой урны случайным образом вынимают 3 шара и опускают во вторую урну. После этого из второй урны также случайно вынимают 4 шара. Найти вероятность того, что все шары, вынутые из второй урны, белые.
1.42. Из п экзаменационных билетов студент А подготовил только т (т<п). В каком случае вероятность вытащить на экзамене «хороший» для него билет выше: когда он берет наудачу билет первым, или вторым,..., или k -тым (к<п) по счету среди сдающих экзамен?
1.43. В лифт семиэтажного дома на первом этаже вошли три человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятность того, что все пассажиры выйдут:
а) на четвертом этаже;
б) на одном и том же этаже;
в) на разных этажах.
1.44. Батарея, состоящая из 3 орудий, ведет огонь по группе, состоящей из 5 самолетов. Каждое орудие выбирает себе цель случайно и независимо от других. Найти вероятность того, что все орудия будут стрелять:
а) по одной и той же цели;
б) по разным целям.
1.45. 20 человек случайным порядком рассаживаются за столом. Найти вероятность того, что два фиксированных лица А и В окажутся рядом, если:
а) стол круглый;
б) стол прямоугольный, а 20 человек рассаживаются случайно вдоль одной из его сторон.
1.46. Имеется коробка с девятью новыми теннисными мячами. Для игры берут три мяча; после игры их кладут обратно. При выборе мячей игранные от неигранных не отличаются. Какова вероятность того, что после трех игр в коробке не останется неигранных мячей?
1.47. Завод выпускает определенного типа изделия; каждое изделие имеет дефект с вероятностью 0,7. После изготовления изделие осматривается последовательно тремя контролерами, каждый из которых обнаруживает дефект с вероятностями 0,8; 0,85; 0,9 соответственно. В случае обнаружения дефекта изделие бракуется. Определить вероятность того, что изделие:
1) будет забраковано;
2) будет забраковано:
а) вторым контролером;
б) всеми контролерами.
1.48. Из полной колоды карт (52 карты) выбирают шесть карт; одну из них смотрят; она оказывается тузом, после чего ее смешивают с остальными выбранными картами. Найти вероятность того, что при втором извлечении карты из этих шести мы снова получим туз.
1.49. В урне два белых и три черных шара. Два игрока поочередно вынимают из урны по шару, не вкладывая их обратно. Выигрывает тот, кто раньше получит белый шар. Найти вероятность того, что выиграет первый игрок.
1.50. Производятся испытания прибора. При каждом испытании прибор выходит из строя с вероятностью 0,8. После первого выхода из строя прибор ремонтируется; после второго признается негодным. Найти вероятность того, что прибор окончательно выйдет из строя в точности при четвертом испытании.
1.51. Имеется 50 экзаменационных билетов, каждый из которых содержит два вопроса. Экзаменующийся знает ответ не на все 100 вопросов, а только на 60. Определить вероятность того, что экзамен будет сдан, если для этого достаточно ответить на оба вопроса из своего билета, или на один вопрос из своего билета, или на один (по выбору преподавателя) вопрос из дополнительного билета.
1.52. Прибор состоит из двух узлов: работа каждого узла безусловно необходима для работы прибора в целом. Надежность (вероятность безотказной работы в течение времени t) первого узла равна 0,8, второго – 0,9. Прибор испытывался в течение времени t, в результате чего обнаружено, что он вышел из строя (отказал). Найти вероятность того, что отказал только первый узел, а второй исправен.
1.53. В группе из 10 студентов, пришедших на экзамен, 3 подготовлено отлично, 4 – хорошо, 2 – посредственно и 1 – плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный – на 16, посредственно – на 10, плохо – на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что студент подготовлен:
а) отлично;
б) плохо.
ГЛАВА
Повторные независимые испытания
В главе рассматриваются:
- формула Бернулли;
- формула Пуассона;
- локальная и интегральная формулы Муавра-Лапласа.
Типовые задачи
Пример 2.1
В среднем 20% пакетов акций на аукционах продаются по первоначально заявленной цене. Найти вероятность того, что из 9 пакетов акций в результате торгов по первоначально заявленной цене:
1) не будут проданы 5 пакетов;
2) будет продано:
а) менее 2 пакетов;
б) не более 2;
в) хотя бы 2 пакета;
г) наивероятнейшее число пакетов.
Решение
1) Вероятность того, что пакет акций не будет продан по первоначально заявленной цене, р = 1-0,2 = 0,8.
По формуле Бернулли (2.1)

2.а) По условию p = 0,2
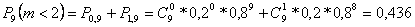
2.б) 
2.в) 
Указанную вероятность можно найти проще, если перейти к противоположному событию, т.е.
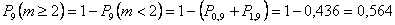 (см.п.2а).
(см.п.2а).
2.г) Наивероятнейшее число проданных акций по первоначально заявленной цене определится из условий (2.4), т.е.
9*0,2-0,8 ≤ m0 ≤ 9*0,2+0,2 или 1≤ m0 ≤ 2,
т.е. наивероятнейших чисел два: m0 = 1 и  = 2.
= 2.
Поэтому вероятность

Пример 2.2
Завод отправил на базу 10000 стандартных изделий. Среднее число изделий, повреждаемых при транспортировке, составляет 0,02%. Найти вероятность того, что из 10000 изделий:
1) будет повреждено:
а) 3;
б) по крайней мере 3;
2) не будет повреждено:
а) 9997;
б) хотя бы 9997.
Решение
1.а) Вероятность того, что изделие будет повреждено при транспортировке, равна р = 0,0002. Так как р – мала, n = 10000 – велико и λ = n*p = 10000*0,0002 = 2≤10, следует применить формулу Пуассона (2.6):
 .
.
Это значение проще найти, используя табл. III приложений:
P3,10000 = P3(2) = 0,1804
1.б) Вероятность P10000(m ≥ 3) может быть вычислена как сумма большого количества слагаемых:
P10000(m ≥ 3) = P3,10000+ P4,10000+…+ P10000,10000.
Но, разумеется, проще ее найти, перейдя к противоположному событию:
P10000(m ≥ 3) = 1 - P10000(m < 3) = 1 - (P0,10000+P1,10000+ P2,10000) = 1-(0,1353+0,2707+0,2707) = 0,3233.
Следует отметить, что для вычисления вероятности P10000(m ≥ 3) = P10000(3 ≤ m ≤ 10000) нельзя применить интегральную формулу Муавра-Лапласа, так как не выполнено условие ее применимости, ибо npq ≈ 2 < 20.
2.а) В данном случае p = 1-0,0002 = 0,9998 и надо найти P9997,10000, для непосредственного вычисления которой нельзя применить ни формулу Пуассона (р велика), ни локальную формулу Муавра-Лапласа (npq ≈ 2 < 20). Однако событие «не будет повреждено 9997 из 10000», вероятность которого, равна 0,1804, получена в 1.а).
2.б) Событие «не будет повреждено хотя бы 9997 из 10000» равносильно событию «будет повреждено не более 3 из 10000», для которого p = 0,0002 и
P10000(m ≤ 3) = P0,10000+ P1,10000+ P2,10000+ P3,10000 = 0,1353+0,2707+0,2707+0,1805 = 0,8572.
Пример 2.3
По результатам проверок налоговыми инспекциями установлено, что в среднем каждое второе малое предприятие региона имеет нарушение финансовой дисциплины. Найти вероятность того, что из 1000 зарегистрированных в регионе малых предприятий имеют нарушения финансовой дисциплины:
а) 480 предприятий;
б) наивероятнейшее число предприятий;
в) не менее 480;
г) от 480 до 520
Решение
а) По условию р = 0,5. Так n = 1000 достаточно велико (условие npq = 10000*0,5*(1-0,5) = 250 ≥ 20 выполнено), то применяем локальную формулу Муавра-Лапласа. Вначале по (2.9) определим
 ,
,
затем по формуле (2.7)

б) По формуле (2.6) наивероятнейшее число 1000*0,5-0,5 ≤ m0 ≤ 1000*0,5+0,5, т.е. 499,5≤m0≤500,5 и целое m0 = 500.
Теперь по (2.9) определим
 и
и 
в) Необходимо найти
P1000(
m≥480) =
P1000(480 ≤
m ≤ 1000). Применяем интегральную формулу Муавра-Лапласа (2.10), предварительно найдя по формуле (2.12)
 ,
, 
Теперь
P1000 (480≤ m ≤1000) ≈  [Ф(31,6) – Ф(-1,265)] =
[Ф(31,6) – Ф(-1,265)] =  [Ф(31,6) + Ф(1,265)] ≈
[Ф(31,6) + Ф(1,265)] ≈  *(1+0,7941) ≈ 0,897.
*(1+0,7941) ≈ 0,897.
г) Вероятность Р1000(480 ≤ m ≤520) можно было найти по той же интегральной формуле Муавра–Лапласа (2.10). Но проще это сделать, используя следствие (2.13), заметив, что границы интервала 480 и 520 симметричны относительно значения пр = 1000*0,5 = 500:

Пример 2.4
В страховой компании 10 тыс. клиентов. Страховой взнос каждого клиента составляет 500 руб. При наступлении страхового случая, вероятность которого по имеющимся данным и оценкам экспертов можно считать равной р = 0,005, страховая компания обязана выплатить клиенту страховую сумму размером 50 тыс. руб. На какую прибыль может рассчитывать страховая компания с надежностью 0,95?
Решение
Размер прибыли компании составляет разность между суммарным взносом всех клиентов и суммарной страховой суммой, выплаченной n0клиентам при наступлении страхового случая, т.е.
П = 500*10-50n0 = 50(100-n0) тыс.руб.
Для определения n0применим интегральную формулу Муавра-Лапласа (требование npq = 10000*0,005*0,995 = 49,75 > 20 выполнено).
По условию задачи
 , (2.17)
, (2.17)
где т – число клиентов, которым будет выплачена страховая сумма;
 ,
, 
откуда

Из соотношения (2.17)
Ф(х2) = 1,9 + Ф(х1) = 1,9 + Ф(-7,09) ≈ 1,9+(-1) = 0,9
По табл. II приложений Ф(х2) = 0,9 при х2 = 1,645
Теперь 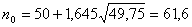 и
и  ,
,
т.е. с надежностью 0,95 ожидаемая прибыль составит 1,92 млн.руб.
Задания
2.1. Вероятность малому предприятию быть банкротом за время t равна 0,2. Найти вероятность того, что из шести малых предприятий за время t сохранятся:
а) два;
б) более двух.
2.2. В среднем пятая часть поступающих в продажу автомобилей некомплектны. Найти вероятность того, что среди десяти автомобилей имеют некомплектность:
а) три автомобиля;
б) менее трех.
2.3. Производится залп из шести орудий по некоторому объекту. Вероятность попадания в объект из каждого орудия равна 0,6. Найти вероятность ликвидации объекта, если для этого необходимо не менее четырех попаданий.
2.4. В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из десяти договоров с наступлением страхового случая будет связано с выплатой страховой суммы:
а) три договора;
б) менее двух договоров.
2.5. Предполагается, что 10% открывающихся новых малых предприятий прекращают свою деятельность в течение года. Какова вероятность того, что из шести малых предприятий не более двух в течение года прекратят свою деятельность?
2.6. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
а) не менее трех мальчиков;
б) не более трех мальчиков.
2.7. Два равносильных противника играют в шахматы. Что более вероятно:
а) выиграть 2 партии из 4 или 3 партии из 6;
б) не менее 2 партий из 6 или не менее 3 партий из 6?
(Ничьи в расчет не принимаются.)
2.8. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено:
а) три ошибочно укомплектованных пакета;
б) не более трех пакетов.
2.9. Строительная фирма, занимающаяся установкой летних коттеджей, раскладывает рекламные листки по почтовым ящикам. Прежний опыт работы компании показывает, что примерно в одном случае из двух тысяч следует заказ. Найти вероятность того, что при размещении 100 тыс. листков число заказов будет:
а) равно 48;
б) находиться в границах от 45 до 55.
2.10. В вузе обучаются 3650 студентов. Вероятность того, что день рождения студента приходится на определенный день года, равна 1/365. Найти: а) наиболее вероятное число студентов, родившихся 1 мая, и вероятность такого события; б) вероятность того, что по крайней мере 3 студента имеют один и тот же день рождения.
2.11. Учебник издан тиражом 10 000 экземпляров. Вероятность того, что экземпляр учебника сброшюрован не правильно, равна 0,0001. Найти вероятность того, что:
а) тираж содержит 5 бракованных книг;
б) по крайней мере 9998 книг сброшюрованы правильно.
2.12. Баскетболиста делают по 3 броска мячом в корзину. Вероятности попадания мяча в корзину при каждом броске равны соответственно 0,6 и 0,7. Найти вероятность того, что:
а) у обоих будет одинаковое количество попаданий;
б) у первого баскетболиста будет больше попаданий, чем у второго.
2.13. Известно, что в среднем 60% всего числа изготовляемых заводом телефонных аппаратов является продукцией первого сорта. Чему равна вероятность того, что в изготовленной партии окажется:
а) 6 аппаратов первого сорта, если партия содержит 10 аппаратов;
б) 120 аппаратов первого сорта, если партия содержит 200 аппаратов?
2.14. Вероятность того, что перфокарта набита оператором неверно, равна 0,1. Найти вероятность того, что:
а) из 200 перфокарт правильно набитых будет не меньше 180;
б) у того же оператора из десяти перфокарт будет неверно набитых не более двух.
2.15. Аудиторную работу по теории вероятностей с первого раза успешно выполняют 50% студентов. Найти вероятность того, что из 400 студентов работу успешно выполнят:
а) 180 студентов;
б) не менее 180 студентов.
2.16. При обследовании уставных фондов банков установлено, что пятая часть банков имеют уставный фонд свыше 100 млн. руб. Найти вероятность того, что среди 1800 банков имеют уставный фонд свыше 100 млн. руб.:
а) не менее 300;
б) от 300 до 400 включительно.
2.17. Сколько нужно взять деталей, чтобы наивероятнейшее число годных деталей было равно 50, если вероятность того, что наудачу взятая деталь будет бракованной, равна 0,1?
2.18. Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,01. Найти наиболее вероятное число опоздавших из 800 пассажиров и вероятность такого числа опоздавших.
2.19. Вероятность того, что деталь стандартна, равна р = 0,9. Найти:
а) с вероятностью 0,9545 границы (симметричные относительно р), в которых заключена доля стандартных среди проверенных 900 деталей;
б) вероятность того, что доля нестандартных деталей среди них заключена в пределах от 0,08 до 0,11.
2.20. В результате проверки качества приготовленных для посева семян гороха установлено, что в среднем 90% всхожи. Сколько нужно посеять семян, чтобы с вероятностью 0,991 можно было ожидать, что доля взошедших семян отклонится от вероятности взойти каждому семени не более, чем на 0,03 (по абсолютной величине)?
2.21. Вероятность того, что дилер, торгующий ценными бумагами, продаст их, равна 0,7. Сколько должно быть ценных бумаг, чтобы можно было утверждать с вероятностью 0,996, что доля проданных среди них отклонится от 0,7 не более, чем на 0,04 (по абсолютной величине)?
2.22. У страховой компании имеются 10 000 клиентов. Каждый из них, страхуясь от несчастного случая, вносит 500 руб. Вероятность несчастного случая 0,0055, а страховая сумма, выплачиваемая пострадавшему, составляет 50 000 руб. Какова вероятность того, что:
а) страховая компания потерпит убыток;
б) на выплат страховых сумм уйдет более половины всех средств поступивших от клиентов?
2.23. Первый прибор состоит из 10 узлов, второй из 8 узлов. За время tкаждый из узлов первого прибора выхода из строя, независимо от других, с вероятностью 0,1, второго – с вероятностью 0,2. Найти вероятность того, что за время t в первом приборе выйдет из строя хотябы один узел, а во втором – по крайней мере два узла.
2.24. Студент рассматриваемого вуза по уровню подготовленности с вероятностью 0,3 является «слабым», с вероятностью 0,5 – «средним», с вероятностью 0,2 – «сильным». Какова вероятность того, что из наудачу выбранных 6 студентов вуза:
а) число «слабых», «средних» и «сильных» окажется одинаковым;
б) число «слабых» и «сильных» окажется одинаковым?
ГЛАВА
Случайные величины
В главе рассматриваются:
- понятие случайной величины, непрерывной случайной величины;
- закон распределения дискретной случайной величины;
- математическое ожидание дискретной случайной величины;
- дисперсия дискретной случайной величины;
- функция распределения случайной величины;
- плотность вероятности;
- мода, медиана, квантили и моменты случайных величин.
Типовые задачи
Пример 3.1
По многолетним статистическим данным известно, что вероятность рождения мальчика равна 0,515. Составить закон распределения случайной величины X – числа мальчиков в семье из 4 детей. Найти математическое ожидание и дисперсию этой случайной величины.
Решение
Число мальчиков в семье из п = 4 представляет случайную величину Х смножеством значений X= т = 0, 1, 2, 3, 4, вероятности которых определяются по формуле Бернулли:
 , где q = 1-p
, где q = 1-p
В нашем случае n = 4, p = 0,515, q = 1-p = 0,485
Вычислим
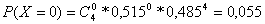 ;
;
 ;
;
 ;
;
 ;
;
 .
.
(Здесь учтено, что  = 1,
= 1, 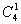 = 4,
= 4, 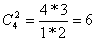 ,
,  ,
,  = 1)
= 1)
Ряд распределения имеет вид
| X = m | xi | |||||
| pi | 0,055 | 0,235 | 0,375 | 0,265 | 0,070 |
Убеждаемся, что 
Математическое ожидание М{Х) и дисперсию D(X)можно найти, как обычно, по формулам (3.3) и (3.11). Но в данном случае, учитывая, что закон распределения случайной величины X биномиальный, можно воспользоваться простыми формулами (4.2) и (4.3):
M(X) = np = 4*0,515 = 2,06,
D(X) = npq = 4*0,515*0,485 = 0,999.
Пример 3.2
Радист вызывает корреспондента, причем каждый последующий вызов производится лишь в том случае, если предыдущий вызов не принят. Вероятность того, что корреспондент примет вызов, равна 0,4. Составить закон распределения числа вызовов, если:
а) число вызовов не более 5;
б) число вызовов не ограничено.
Найти математическое ожидание и дисперсию этой случайной величины.
Решение:
а) Случайная величина X – число вызовов корреспондента – может принимать значения 1, 2, 3, 4, 5. Обозначим событие Ai –
i -й вызов принят (i = 1, 2, 3, 4, 5). Тогда вероятность того, что первый вызов принят, P(
X=1)=
P(
A1)=0,4.
Второй вызов состоится лишь при условии, что первый вызов не принят, т.е.

Аналогично


Пятый вызов при любом исходе (будет принят, не принят) I последний. Поэтому

(Вероятность Р(Х=5) можно найти и иначе, учитывая, что последний вызов будет или принят, или нет, т.е.
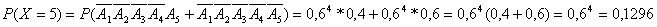 )
)
Ряд распределения случайной величины X имеет вид
| X: | xi | |||||
| pi | 0,4 | 0,24 | 0,144 | 0,0864 | 0,1296 |
Проверяем, что 
По формуле (3.3) вычислим математическое ожидание:

Так как M(X) – нецелое число, то находить дисперсию D(X) проще не по основной формуле (3.11), а по формуле (3.16), т.е. D(X) = M(X2) – а2.
Вычислим

Теперь D(X) = 7,2784 – 2,30562 = 1,9626
б) Так как число вызовов не ограничено, то ряд распределения случайной величины Х примет вид
| X: | xi | … | n | … | ||||
| pi | 0,4 | 0,24 | 0,144 | 0,0864 | … | 0,6n-1*0,4 | … |
Проверяем, что

(использовали формулу суммы сходящегося (│q│< 1) геометрического ряда:  при a = 1, q= 0,6)
при a = 1, q= 0,6)
По формуле (3.4) вычислим математическое ожидание


Для вычисления суммы полученного ряда воспользуемся формулой:
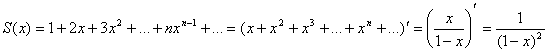
(т.е. сумма данного ряда является производной сходящегося геометрического ряда при│q│=│x│<1). При х = 0,6.
 , т.е. M(
, т.е. M(
X) = 0,4*6,25 = 2,5
По формуле (3.12) вычислим дисперсию: D(X) = M(
X2) –
a2.
Вначале найдем


Для вычисления суммы полученного ряда рассмотрим сумму ряда
S1(x) при │х│< 1:


S1(x) при х = 0,6:
 , т.е. M(X2) = 0,4*25=10
, т.е. M(X2) = 0,4*25=10
Теперь D(X) = 10-2,52 = 3,75.
Пример 3.3
Среди 10 изготовленных приборов 3 неточных. Составить закон распределения числа неточных приборов среди взятых наудачу четырех приборов. Найти математическое ожидание и дисперсию этой случайной величины.
Решение
Случайная величина X – число неточных приборов среди четырех отобранных – может принимать значения i - 0, 1, 2, 3.
Общее число способов выбора 4 приборов из 10 определяется числом сочетаний  . Число способов выбора четырех приборов, среди которых i неточных приборов и 4- i точных (i = 0, 1, 2, 3), по правилу произведения определится произведением числа способов выбора i неточных приборов из 3 неточных
. Число способов выбора четырех приборов, среди которых i неточных приборов и 4- i точных (i = 0, 1, 2, 3), по правилу произведения определится произведением числа способов выбора i неточных приборов из 3 неточных  на число способов выбора 4- i точных приборов из 7 точных
на число способов выбора 4- i точных приборов из 7 точных  , т.е.
, т.е.  *
*  . Согласно классическому определению вероятности
. Согласно классическому определению вероятности
 (i = 0, 1, 2, 3).
(i = 0, 1, 2, 3).
Учитывая, что  = 1,
= 1,  = 3,
= 3, 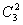 =
=  = 3,
= 3,  = 1,
= 1,
 ,
,  ,
,  ,
,
 .
.
Вычислим

т.е. ряд распределения будет такой:
| X: | xi | ||||
| pi | 1/6 | 1/2 | 3/10 | 1/30 |
Убеждаемся в том, что 
Математическое ожидание M(
X) и дисперсию D(
X) вычисляем по формулам (3.3) и (3.16):
 ,
,
 и
и
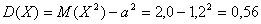 .
.
Пример 3.4
Ряд распределения дискретной случайной величины состоит из двух неизвестных значений. Вероятность того, что случайная величина примет одно из этих значений, равна 0,8. Найти функцию распределения случайной величины, если ее математическое ожидание равно 3,2, а дисперсия 0,16.
Решение
Ряд распределения имеет вид
| X: | xi | x1 | x2 |
| pi | 0,8 | 0,2 |
,
где pi = 0,8, а p2 = 1-p1 = 1-0,8 = 0,2.
По условию

или

Решая полученную систему, находим два решения:
 и
и 
Записываем выражение функции распределения:

 или
или 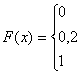

Пример 3.5
Рабочий обслуживает 4 станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, для первого станка равна 0,9, для второго – 0,8, для третьего -0,75 и для четвертого – 0,7. Составить закон распределения случайной величины X – числа станков, которые не потребуют внимания рабочего в течение часа.
Решение
Задача может быть решена несколькими способами.
Первый способ: Пусть 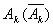 – событие, состоящее в том, что k -й станок не потребует (потребует) внимания рабочего в течении часа. Тогда, очевидно:
– событие, состоящее в том, что k -й станок не потребует (потребует) внимания рабочего в течении часа. Тогда, очевидно:
 ;
;

 .
.
Аналогично находим
 ;
;

 ,
,
т.е. закон (ряд) распределения случайной величины Х имеет вид:
| X: | xi | |||||
| pi | 0,0015 | 0,0275 | 0,1685 | 0,4245 | 0,378 |
(3.38)
Второй способ состоит в том, что заданы законы (ряды) распределения альтернативных случайных величин X k (
k =1,2,3,4), выражающих число станков, не потребующих внимания рабочего в течение часа (это число для каждого станка равно 1, если этот станок не потребует внимания рабочего, и равно 0, если потребует):
X1: X2: X3: X4:
| xi | xi | xi | xi | |||||||||||
| pi1 | 0,1 | 0,9 | pi2 | 0,2 | 0,8 | pi3 | 0,25 | 0,75 | pi4 | 0,3 | 0,7 |
Необходимо найти закон распределения суммы этих случайных величин, т.е. Х = Х1 + Х2 + Х3 + Х4. Суммируя последовательно Х1 + Х2 = Z, Х1 + Х2 + Х3 = Z + X3 = U, Х1 + Х2 + Х3 + Х4 = U + X4 = X, получим
Z = Х1 + Х2:
| zi | |||
| pi | 0,02 | 0,26 | 0,2 |
U = Z + X3:
| um | ||||
| pm | 0,005 | 0,08 | 0,375 | 0,54 |
и, наконец, распределение X = U + X4, т.е. получили (3.38).
Третий способ: Распределение Х можно получить чисто механически, перемножив биномы (двучлены):
 , (3.39)
, (3.39)
причем каждый из пяти полученных коэффициентов при zk (k = 0, 1, 2, 3, 4) в функции φ4(
z) будет выражать соответствующие вероятности P(
X =
k). Действительно, преобразовав (3.39), получим
 ,
,
где коэффициенты – это вероятности значений случайной величины Х (3.38).
Пример 3.6
В 1-й урне содержится 6 белых и 4 черных шара, а во 2-й –3 белых и 7 черных шаров. Из 1-й урны берут на удачу два шара и перекладывают во 2-ю урну, а затем из 2-й урны берут наудачу один шар и перекладывают в 1-ю урну. Составить законы распределения числа белых шаров в 1-й и 2-й урнах.
Решение
Найдем закон распределения случайной величины X






