Рассмотрим совокупность (в математике принято говорить – систему) векторов а 1, а 2, …, а k линейного пространства L.
Выражение вида 
называют линейной комбинацией векторов этой системы, а числа a1, a2, …, a k – коэффициентами этой линейной комбинации.
Если 
, то говорят, что вектор а линейно выражается через векторы а 1, а 2, …, а k или что вектор а является линейной комбинацией векторов а 1, а 2, …, а k.
Определение 2
Система а 1, а 2, …, а k векторов линейного пространства L называется линейно зависимой, если найдутся числа a1, a2 ,…,a k, среди которых хотя бы одно не равно нулю, такие что 
.
В этом случае говорят также, что векторы а 1, а 2, …, а k линейно зависимы.
Определение 3
Система а 1, а 2, …, а k векторов линейного пространства L называется линейно независимой, если равенство выполняется лишь при условии, что a1= a2 = …= a k = 0.
В этом случае также говорят, что векторы а 1, а 2, …, а k линейно независимы.
Сформулируем без доказательства критерий линейной зависимости
Теорема 1
Система векторов а 1, а 2, …, а k линейно зависима тогда и только тогда, когда хотя бы один из векторов этой системы можно представить в виде линейной комбинации остальных векторов.
Из теоремы 1 следует, что система векторов а 1, а 2, …, а k линейно независима тогда и только тогда, когда ни один из векторов этой системы не является линейной комбинацией остальных.
Линейно независимая система векторов а 1, а 2, …, а k называется максимально линейно независимой, если для любого вектора b ÎL система а 1, а 2, …, а k, b – линейно зависима.
Для примера рассмотрим пространство V2. Любые два неколлинеарных вектора этого пространства линейно независимы. Действительно, предположим, что неколлинеарные векторы 
и 
линейно зависимы. Тогда существуют такие числа a и b, не равные одновременно нулю, что 
. Пусть b ¹ 0. Тогда из предыдущего равенства находим b = – a или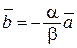 
, а это означает, что векторы и коллинеарны, что противоречит нашему предположению. Следовательно, неколлинеарные векторы и линейно независимы.
Любые три вектора пространства V2 линейно зависимы. Докажем это. Пусть 
, , 
– три вектора, лежащие в одной плоскости. Достаточно рассмотреть следующие случаи.
а) Пусть один из этих векторов нулевой, например, =` 0, тогда очевидно равенство
0 + 0 + 1 
=` 0,
значит, существует нетривиальная линейная комбинация рассмотренных векторов, равная нулевому вектору. Следовательно, рассмотренные векторы линейно зависимы.
б) Пусть , , 
– ненулевые и два из них коллинеарны, например, || . Тогда 
, 
, откуда 
, это означает, что есть линейная комбинация векторов и . Следовательно, согласно теореме 2.1, векторы , , линейно зависимы.
|
|
, , – ненулевые и попарно неколлинеарны. Отложим их от одной точки О: 
, 
, 
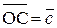(рисунок 8). Через точку С
|
|
|
|
|
|
|
и , точки пересечения обозначим соответственно А1 и В1. Тогда векторы 
и 
коллинеарны соответственно векторам и . Следовательно, существуют числа a и b 
такие, что = a и = b . С другой стороны, вектор 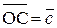есть диагональ параллелограмма ОА1СВ1 и значит, равен сумме векторов и :
= + = a + b . (*)
Таким образом, вектор есть линейная комбинация векторов и , следовательно, векторы , , – линейно зависимые.
Если взять систему из большего числа векторов , , , 
, …, 
, то из равенства (*), доказанного для произвольных трех векторов, следует
= a + b + 
.
Это означает, что система , , , , …, линейно зависима.
Таким образом, в пространстве V2 максимально линейно независимую систему образуют два неколлинеарных вектора.
Определение 2
Базисом линейного пространства L называется упорядоченная максимально линейно независимая система а 1, а 2, а 3, …, а п векторов этого пространства. Число n векторов базиса называется размерностью линейного пространства, само пространство при этом называется п -мерным.
Если хотят подчеркнуть, что линейное пространство Lимеет размерность п, пишут L n. Линейное пространство, базис которого состоит из конечного числа векторов, называют конечномерным. Линейное пространство называют бесконечномерным, если для всякого натурального п в этом пространстве найдется п линейно независимых векторов.
Заметим, что если размерность линейного пространства равна п, то любые п линейно независимых векторов линейного пространства образуют базис этого пространства. Каждое п -мерное линейное пространство имеет бесконечно много базисов и все они состоят из п векторов.
Рассмотрим примеры базисов некоторых линейных пространств.
1. Выше было доказано, что в пространстве V2 максимально линейно независимую систему образуют два неколлинеарных вектора. Следовательно, пространстве V2 базис образует любая упорядоченная система двух неколлинеарных векторов.
2. В пространстве V3 базис образует любая упорядоченная система трех некомпланарных векторов. Доказательство можно провести аналогично тому, как это было сделано для пространства V2.
3. Рассмотрим пространство R n числовых строк длины п. Покажем, что векторы
=[1, 0, 0, …, 0], 
= [0, 1, 0,…, 0], …, 
=[0, 0, 0, …,1]
образуют линейно независимую систему. Для этого рассмотрим произвольную линейную комбинацию этих векторов и выясним, при каких значениях коэффициентов выполняется равенство:
.
или
a1[1, 0, 0, …, 0] + a2[0, 1, 0,…, 0] + … + a п [0, 0, 0, …,1] = [0, 0,…, 0].
Выполнив действия над векторами в левой части равенства, получим
[a1, a2, …, a n ] = [0, 0,…, 0],
откуда, очевидно, a1= 0, a2= 0, …, a п = 0. Это значит, что равенство выполняется лишь при условии a1= 0, a2= 0, …, a п = 0, откуда следует, что рассматриваемая система векторов линейно независима. Покажем, что эта система максимально линейно независима.
Пусть х = [ х 1, х 2, …, х п ] – произвольный вектор пространства R n. Очевидно, можно записать
[ х 1, х 2, …, х п ] = х 1[1, 0,…, 0] + х 2[0, 1,…, 0] + … + хп [0, 0,…, 1]. (**)
А это значит, вектор х есть линейная комбинация векторов 
. Таким образом, в пространстве R n система векторов , х линейно зависима для любого вектора х. Значит, система максимально линейно независима, и значит, образует базис пространства R n.
Теорема 2
Если система а 1, а 2, …, а п есть базис линейного пространства L, то, для любого вектора х ÎL существуют единственная система чисел a1, a2, …, a п таких, что
, (1)
т.е. любой вектор пространства единственным образом представим в виде линейной комбинации векторов базиса.
Если а 1, а 2, …, а п – базис линейного пространства L, а х – произвольный вектор пространства L, то равенство
х = a1 а 1+ a2 а 2+ …+ a п а п
называется разложением вектора х по базису а 1, а 2, …, а п. Коэффициенты этого разложения a1, a2, …, a п называются координатами вектора х в заданном базисе.
Тот факт, система векторов а 1, а 2, …, а п есть базис пространства, будем записывать Б: { а 1, а 2, а 3, …, а п }, а то, что числа a1, a2, …, a п являются координатами вектора х в базисе Б:{ а 1, а 2, …, а п } будем обозначать
х = (a1, a2, …, a п)Б или х Б = (a1, a2, …, a п).
Строку (a1, a2, …, a п) называют координатной строкой вектора х в заданном базисе
Если векторы линейного пространства L заданы своими координатами в некотором базисе, то линейные операции над этими векторами сводятся к операциям над их координатами. При этом:
1) нулевой вектор в любом базисе имеет нулевые координаты:
0 = (0, 0, …, 0);
2) два вектора равны тогда и только тогда, когда равны их соответствующие координаты:
х = у Û a1 = b1,a2 =b2, …, a п = b п.
3) координаты суммы векторов равны сумме соответствующих координат слагаемых: если х = (a1,a2, …, a п), у = (b1,b2, …, b п), то
х + у = (a1 + b1,a2 +b2, …, a п + b п).
4) координаты произведения вектора на число равны произведениям координат векторана это число: если х = (a1, a2, …, a п), l – число, то
l х = (la1,la2, …, la п)
Заметим, что строка (a1, a2, …, a п) есть вектор линейного пространства R n числовых строк длины п. Таким образом, мы установили взаимно однозначное соответствие между элементами произвольного п -мерного линейного пространства L и пространства R n числовых строк длины п. Поэтому любые действия с векторами рассматриваемого линейного пространства могут быть заменены соответствующими действиями над координатами этих векторов в выбранном базисе, т.е. над векторами пространства R n.
Договоримся о следующих обозначениях.
Если речь будет идти о векторах ЛП R n, то будем их обозначать [ х 1, х 2, …, хп ] (т.е. компоненты числовой строки будем писать в квадратных скобках). Если же эта числовая строка определяет координаты некоторого вектора п -мерного ЛП в заданном базисе, то будем писать(х 1, х 2, …, хп), т.е., как и раньше, координаты вектора будем писать в круглых скобках.
Очевидно, что координаты вектора зависят от выбора базиса: один и тот же ненулевой вектор в разных базисах имеет разные координаты. Поэтому, записывая вектор в координатной форме, нужно всегда оговаривать, в каком базисе эти координаты заданы.
В каждом линейном пространстве из множества всевозможных базисов можно выделить такой, разложение по которому векторов пространства осуществляется наиболее просто. Такие базисы называют каноническими (от греческого χανων – канон, правило, образец, норма). Будем обозначать канонический базис Бк. Например, в пространстве R n координаты произвольного вектора х = равны его компонентам, что следует из равенства (**). Поэтому в пространстве R n канонический базис образуют векторы
=[1, 0, 0, …, 0], = [0, 1, 0,…, 0], …, =[0, 0, 0, …,1].
Без доказательства отметим, что в пространстве R п (x) многочленов степени не выше п базис образуют любые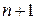 
линейно независимых многочлена. Канонический базис Бк этого пространства образуют векторы-многочлены
1, x, x 2, …, xn
Действительно, любой вектор-многочлен
,
фактически, уже разложен по этому базису
,
Следовательно, координаты вектора Р (х) в базисе Бк:{1, x, x 2, …, xn } имеют вид (а 0, а 1, …, ап), т.е. равны коэффициентам этого многочлена, взятым в порядке, соответствующем порядку векторов в базисе.
В ЛП М2 матриц второго порядка канонический базис образуют матрицы 
, 
, 
, 
.
