Элементы комбинаторики
Факториал n! = n × (n - 1) × (n – 2) × (n - 3)×…× 2 × 1; 0! = 1.
Перестановки P n = n!
Пример. Сколькими способами можно разместить на полке три книги?
В данной задаче необходимо найти число перестановок из четырех элементов. Существует четыре варианта выбора первой книги. Далее остается три варианта выбора второй книги, два варианта третьей книги и один способ выбора четвертой книги.
Таким образом, число способов N разместить четыре книги на полке равно произведению чисел 4, 3, 2 и 1, т. е.
способа.
Определение. Размещениями из n элементов по k (n³k) называют множество комбинаций из k элементов, выбираемых из n элементов, отличающихся составом или порядком.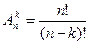 
Пример. Сколько двухбуквенных комбинаций, не содержащих повторений, можно составить из 32 букв русского алфавита?
В данной задаче необходимо найти число размещений из 32 элементов по 2 по формуле (3):
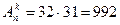двухбуквенных комбинаций.
По данным «Словаря русского языка» из этих 992 комбинаций только 114 являются словами. Например, да, ад, еж, яр и т. д.
Определение. Сочетаниями из n элементов по k (n³k) называют множество комбинаций из k элементов, выбираемых из n элементов, отличающихся составом.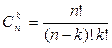 
.
Пример. В соревновании участвуют 12 спортсменов. Сколькими способами можно выбрать трех из них для участия в первом забеге?
При выборе трех спортсменов из двенадцати порядок, в котором их будут выбирать, не играет роли, поэтому число способов, которыми можно выбрать трех из них, для участия в первом забеге найдем с помощью формулы (5):
способов.
.
Пример. В урне 5 белых и 6 красных шариков. Сколькими способами можно выбрать два шарика одного цвета?
В данной задаче необходимо найти число способов N, которыми можно выбрать 2 белых шара из 5 белых шаров или 2 красных шара из 6 красных шаров. Учитывая, что 2 элемента из 5 можно выбрать числом способов равным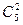 
, а 2 элемента из 6 можно выбрать числом способов равным 
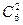и используя формулу (5), имеем:
способов.
Пример. В столовой предлагают два вида первых блюд, три вида вторых блюд и два вида десерта. Сколькими способами можно составить обед из трех блюд?
Обозначим множество первых блюд через А, вторых – В и третьих – С. Обозначив число способов, которыми можно составить обед из трех блюд через N и используя правило произведения, получим:
N = 2 × 3 × 2 = 12 способов.
Пример. В урне 3 красных и 4 синих шариков. Сколькими способами можно выбрать четыре шарика так, чтобы два из них были красными, а два - синими?
Обозначим множество красных шариков через А, синих– В. Обозначив число способов, которыми можно выбрать два красных шарика из множества А и два синих шарика – из множества В, через N и используя правило произведения, получим:
способов.
Пример. В урне 5 красных, 7 белых и 4 зеленых шарика. Сколькими способами можно выбрать три шарика так, чтобы из них хотя бы два были красными?
Обозначим множество красных шариков через А, белых– В, зеленых - C. Вопрос, поставленный в задаче можно сформулировать следующим образом: сколькими способами можно выбрать три шарика так, чтобы было два красных шарика и один белый или два красных шарика и один зеленый или три красных шарика.
Обозначив число способов, которыми можно выбрать три шарика так, чтобы из них хотя бы два были красными через N и, используя правила суммы и произведения, получим:
.
Элементы теории вероятностей
Определение. Случайное событие (событие) − результат испытания, который при реализации определенного комплекса условий может произойти или не произойти.
Например, случайными событиями являются:
· выпадение орла (решки) в испытании, связанном с бросанием монеты;
· выпадение какого-либо числа от 1 до 6, в испытании, связанном с бросанием игральной кости;
· попадание (промах) при стрельбе;
· выпуск бракованного изделия в массовом производстве.
Определение. События, которые при реализации определенного комплекса условий, никогда не могут произойти одновременно в результате одного испытания, называются несовместными.
Например, несовместными являются события, состоящие в одновременном:
· выпадении орла и решки в результате одного бросания монеты;
· выпадении на верхней грани игральной кости чисел 2 и 3 или любых двух чисел от 1 до 6 при ее однократном бросании;
· попадании и промахе при одном выстреле по мишени.
Определение. Два события называются противоположными, если в результате одного испытания всегда происходит одно и только одно из этих событий.
В теории вероятностей событие, противоположное событию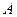 
принято обозначать 
(читается «не »).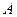
Например, противоположными являются события:
· выпадение орла и выпадение решки в результате одного бросания монеты;
· попадание и промах при одном выстреле по мишени.
Определение. События образуют полную группу, если в каждом испытании реализуется одно и только одно из попарно несовместных событий.
Например, полную группу образуют следующие события:
· выпадении орла или решка в результате одного бросания монеты;
· выпадении чисел от 1 до 6 при однократном бросании игральной кости;
· попадании или промахе при одном выстреле по мишени.
Учитывая, определение понятия несовместных событий противоположные события можно определить иначе.
Определение. Два несовместных события, образующих полную группу, называются противоположными.
Замечание. Понятие несовместных событий является более широким по отношению к понятию противоположных событий. Так как все противоположные события являются несовместными, но не все несовместные события являются противоположными. Например, при однократном бросании игральной кости, выпадение чисел 5 и 6 на ее верхней грани являются событиями несовместными. Однако эти события не являются противоположными, поскольку возможны события, связанные с выпадением чисел от 1 до 4.
Определение. События А и В называются независимыми, если в результате проведения испытания, наступление или ненаступление одного события не влияет наступление или ненаступление другого события.
Например, независимыми являются события, состоящие в:
· выпадении орла на первой монете и решка на второй монете в испытании с бросанием двух монет;
· выпадении орла при первом бросании и орла при втором бросании монеты;
· выпадении числа 6 при первом бросании и числа 2 при втором бросании игральной кости;
· попадание в цель первым, вторым или третьим стрелками.
Алгебра событий
Определение. Суммой событий A и B (A + B) называется такое событие C, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий A или B.
Таблица.1.
Сумма событий A и B
| A | B | A+B |
| + | + | + |
| + | - | + |
| - | + | + |
| - | - | - |
Определение. Произведением событий A и B (A × B) называется такое событие C, которое происходит тогда и только тогда, когда происходят оба события A и B.
Таблица 2.
Произведение событий A и B
| A | B | A×B |
| + | + | + |
| + | - | - |
| - | + | - |
| - | - | - |
