Как было отмечено ранее, движущая сила массообменных процессов определяется степенью отклонения от состояния равновесия, т.е. разностью между рабочей и равновесной концентрациями (или, наоборот, в зависимости от их абсолютных величин).
При расчете массообменных процессов движущую силу процесса и кинетику (т. е. скорость массопередачи) принято выражать следующими способами:
1. Движущая сила выражается через разность концентраций (среднеинтегральную или среднелогарифмическую), а скорость массопередачи - через коэффициенты массопередачи.
2. Движущая сила выражается через число единиц переноса, а скорость массопередачи (кинетика) - через высоту, эквивалентную единице переноса.
3. Движущая сила выражается через число теоретических ступеней контакта или число теоретических тарелок, а скорость массопередачи (кинетика)- через к.п.д. или через высоту, эквивалентную теоретической ступени контакта.
Средняя интегральная разность концентраций.
Если равновесная кривая не является линейной, то средняя движущая сила вычисляется как средняя интегральная разность концентраций и определяется следующим образом. Запишем дифференциальное уравнение материального баланса для фазы G и уравнение массопередачи для элемента поверхности dF 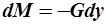 и
и  , откуда
, откуда 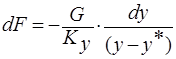 . Интегрируя в пределах O-F,
. Интегрируя в пределах O-F,  , получим при
, получим при 

 .
.
Значение  находится методом графического интегрирования. Для этого берется ряд значений x (см. рис.), находятся соответствующие значения
находится методом графического интегрирования. Для этого берется ряд значений x (см. рис.), находятся соответствующие значения  и вычисляются величины
и вычисляются величины  , строится зависимость
, строится зависимость 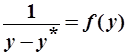 . (рис). Значение интеграла будет равно площади S, умноженной на масштаб a, тогда:
. (рис). Значение интеграла будет равно площади S, умноженной на масштаб a, тогда:
 . Из уравнения
. Из уравнения  выразим G и подставим
выразим G и подставим  , или
, или  (**)
(**)







 Графическое определение
Графическое определение


S
 |

 y
y
Сравним (**) с (ОУМП). Видно, что  (получили выражение для среднеинтегральной движущей силы.)
(получили выражение для среднеинтегральной движущей силы.)
Записав дифференциальное уравнение материального баланса и уравнение массопередачи для фазы L, аналогично найдем:
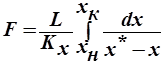 , при
, при  и
и  .
.
Среднелогарифмическая разность концентраций
Если равновесная линия – прямая, проходящая через начало координат х, y, её уравнение можно записать в виде:


Из дифференциального уравнения материального баланса  следует, что
следует, что  . Продифференцируем
. Продифференцируем  , откуда
, откуда  ;
;
 , т.е.
, т.е.  Подставим
Подставим  в дифференциальное уравнение массопередачи
в дифференциальное уравнение массопередачи  , получим
, получим  ;
;  .
.
Проинтегрируем от 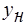 до
до  , 0-F.
, 0-F.
 .(«)
.(«)
Уравнение материального баланса для всего аппарата: 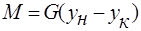 , откуда
, откуда  (*). Для фазы L
(*). Для фазы L  ; с учетом
; с учетом 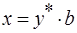 получим
получим  . (**) Сложим (*) и (**), получим
. (**) Сложим (*) и (**), получим 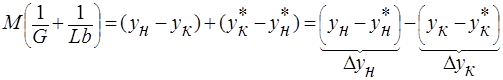 , или
, или 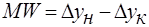 ;
; 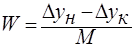 ; Подставим W в («), получим:
; Подставим W в («), получим:  , откуда:
, откуда:
 (!). Сравним (!) с (ОУМП); видим:
(!). Сравним (!) с (ОУМП); видим:
 . Аналогично
. Аналогично 
Число единиц переноса
Интеграл -  имеет определенный физический смысл. Числитель дроби в подинтегральном выражении характеризует изменение рабочей концентрации на элементе поверхности, а
имеет определенный физический смысл. Числитель дроби в подинтегральном выражении характеризует изменение рабочей концентрации на элементе поверхности, а  - движущую силу на этом элементе. Дробь в целом показывает, на сколько единиц изменится рабочая концентрация на данном элементе поверхности при величине движущей силы = 1. Поэтому, число получаемое при подсчете интеграла называется числом единиц переноса и обозначается
- движущую силу на этом элементе. Дробь в целом показывает, на сколько единиц изменится рабочая концентрация на данном элементе поверхности при величине движущей силы = 1. Поэтому, число получаемое при подсчете интеграла называется числом единиц переноса и обозначается 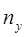 (или
(или  ).
).

 В некоторых случаях, когда поверхность межфазного обмена в аппарате практически неопределима, можно вести расчет по числу единиц переноса. Поверхность межфазного обмена можно представить в виде:
В некоторых случаях, когда поверхность межфазного обмена в аппарате практически неопределима, можно вести расчет по числу единиц переноса. Поверхность межфазного обмена можно представить в виде:
 , где H – высота рабочей зоны аппарата, (м);
, где H – высота рабочей зоны аппарата, (м);
 - площадь поперечного сечения аппарата, (м2);
- площадь поперечного сечения аппарата, (м2);
f – удельная поверхность фазового концентрата, развиваемая в 1 м3 рабочего объема аппарата (м2/м3). Тогда уравнение можно записать:
 . Откуда
. Откуда  .
.
Комплекс  - представляет собой высоту аппарата, эквивалентную единице переноса.
- представляет собой высоту аппарата, эквивалентную единице переноса.
 В окончательном виде расчетное уравнение
В окончательном виде расчетное уравнение  . Аналогично по фазе
. Аналогично по фазе  L:
L: 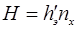 , где
, где  - высота, эквивалентная единице переноса:
- высота, эквивалентная единице переноса:  . Сопоставляя уравнения можно получить:
. Сопоставляя уравнения можно получить:  ,
,  . Для случая, когда линия равновесия прямая
. Для случая, когда линия равновесия прямая  и
и  .
.






