Цель занятия – проверить общее качество уравнения регрессии на основании дисперсионного анализа, научиться находить доверительные интервалы для зависимой переменной.
Организационный момент 3 мин
Предварительный опрос – 7 мин
Выполнение задания на компьютере 30 мин
Форма контроля – тестирование 7 мин
Подведение итогов - 3 мин
СОДЕРЖАНИЕ
1. Проверка общего качества уравнения регрессии. Коэффициент детерминации. 2. Скорректированный коэффициент детерминации.
3. Проверка значимости коэффициента детерминации.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
[1], [3], [4], [5], [6]
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
Задача 3.6 стр 79-80 [5]
Самост. решение упр. 3.10,3.11 стр 80,81 [5]
ТЕСТЫ
1. Проверка значимости уравнения регрессии проводится на основе:
а) корреляционного анализа; б) дисперсионного анализа; в) регрессионного анализа
2. Если значение коэффициента детерминации R2 близко к единице, то:
а) вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, линия регрессии параллельна оси абсцисс;
б) эмпирические точки( )лежат на линии регрессии, между переменными Y X существует линейная функциональная зависимость;
)лежат на линии регрессии, между переменными Y X существует линейная функциональная зависимость;
в) тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии;
3. Что значит проверить значимость уравнения регрессии:
а) проверить, соответствует ли построенная модель моделируемому реальному экономическому объекту или процессу;
б) оценить тесноту корреляционной зависимости;
в) проверить, соответствует ли математическая модель экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных;
г) выразить в математической форме обнаруженные связи и соотношения.
4. В случае парной линейной регрессионной модели коэффициент детерминации равен:
а)  ; б)
; б) 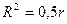 ; в)
; в)  ; г)
; г) 
ТЕСТЫ
1. Если эконометрическая модель содержит несколько объясняющих переменных, она называется:
а) линейной регрессией; б) парной регрессией; в) множественной регрессией; г) моделью временного ряда.
5.В случае, если выборка имеет 27 наблюдений, то при парной линейной регрессии число степеней свободы t – распределения Стьюдента составит:
а) 23; б) 25; в) 27; г) 21.
2.Укажите правильную формулу для определения выборочного коэффициента корреляции:
а) r = 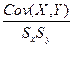 б) r = b1
б) r = b1  в)r =
в)r = 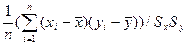
3. Имеются данные о связи между стоимостью основных производственных фондов и объемов валовой продукции по трем однотипным предприятиям (см.табл)
| Основные производственные фонды (х) В млн. тенге | Валовая продукция (y) в млн. тенге |
Используя МНК, найдите неизвестные параметры в стандартном уравнении вида y =  +bx
+bx
а)  б)
б)  г)
г)  в)
в) 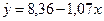
4. По уравнению линейной парной регрессии найден коэффициент детерминации R2 =0,893. Какой вывод можно сделать из найденного коэффициента детерминации:
а) изменения значений зависимой переменной обуславливают 89,3% колеблемости объясняющей переменной X;
б) изменения значений объясняющей переменной X обуславливают 89,3% колеблемости зависимой переменной Y.
в) изменения значений объясняющей переменной X обуславливают 10,7% колеблемости зависимой переменной Y;
г) изменения значений зависимой переменной Y обуславливают 10,7% колеблемости объясняющей переменной X;
5. Дайте экономическую интерпретацию параметрам уравнения  :
:
6. Проверка значимости уравнения регрессии проводится на основе:
а) корреляционного анализа;
б) дисперсионного анализа;
в) регрессионного анализа;
г) нет верного ответа.
7. Оценка вектора  коэффициентов множественной линейной регрессии, полученной по МНК, определяется по формуле:
коэффициентов множественной линейной регрессии, полученной по МНК, определяется по формуле:
а) 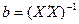 ; б)
; б)  ; в)
; в)  ;
;
8. В некоторой стране годовой доход каждого индивида y определяется по формуле: 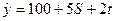 , где S - число лет обучения индивида, t -трудовой стаж (в годах), x - возраст индивида. Рассчитайте cov(x, S) для выборки из 4-х индивидов, описанных ниже:
, где S - число лет обучения индивида, t -трудовой стаж (в годах), x - возраст индивида. Рассчитайте cov(x, S) для выборки из 4-х индивидов, описанных ниже:
| Индивид | Возраст(годы) | Годы обучения | Трудовой стаж | Доход |
а) 3,76 б) 4,02 в) 3,5 г) 3,87
9. Регрессионной зависимостью называется такая зависимость, когда каждому значению одной переменной соответствует:
а) определенное (условное) распределение другой переменной;
б) определенное значение другой переменной;
в) определенное математическое ожидание (среднее значение) другой переменной;
г) односторонняя зависимость случайной переменной Yот одной (или нескольких) неслучайной независимой переменной X.
10. Дайте экономическую интерпретацию параметрам уравнения  , где у – объем валовой продукции, х – стоимость основных производственных фондов:
, где у – объем валовой продукции, х – стоимость основных производственных фондов:
а) с увеличением стоимости основных производственных фондов на один млн. тенге объем валовой продукции увеличится на 7,5%;
б) с увеличением стоимости основных производственных фондов на один млн. тенге объем валовой продукции увеличивается в среднем на 7,5млн. тенге.
в) с увеличением объема валовой продукции на 1 млн. тенге стоимость основных фондов увеличивается в 7,5 млн. тенге;
г) с увеличением стоимости основных производственных фондов на 1% объем валовой продукции уменьшается на 7,5млн. тенге;






