Цель занятия – изучить способы линеаризации переменных в нелинейных эконометрических моделях регрессии, находить параметры уравнения регрессии, научиться оценивать существенность параметров уравнения регрессии.
Организационный момент 3 мин
Постановка задачи, краткий опрос по теме – 7 мин
Выполнение задания на компьютере 25 мин
Форма контроля – защита работы 10 мин
Подведение итогов - 5 мин
СОДЕРЖАНИЕ
1. Нелинейные модели регрессии.
2. Преобразование переменных. Логарифмические, полулогарифмические регрессионные модели.
3. Степенная и другие модели регрессии.
4. Выбор формы эконометрической модели.
5. Оценивание производственных функций.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
[1], [3], [4], [5],[6]
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
Пример 1б, 1в,1г стр 10 -16 [4]
Самост. решение - упр.21, 22, 23, стр 38-43 [4]
ТЕМА № 4. Статистическая значимость коэффициентов линейной регрессии
Цель занятия – научиться определятьстатистическую значимость коэффициентов линейной регрессии, применять для проверки t – статистику Стьюдента, строить доверительные интервалы для зависимой переменной.
Организационный момент 3 мин
Выполнение задания на компьютере 25 мин
Форма контроля – защита работы10 мин
Тестирование – 7 мин
Подведение итогов, д/з - 5 мин
СОДЕРЖАНИЕ
1. Классическая линейная регрессионная модель.
2. Проверка статистической значимости коэффициентов линейной регрессии.
3. t – статистика Стьюдента.
4. Интервальные оценки коэффициентов линейного уравнения регрессии.
5. Доверительные интервалы для зависимой переменной.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
[1], [3], [4], [5], [6]
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
Упр. 3.3. - стр. 68-70 [5]
Д/з упр. 3.7,3.9 - стр. 80,81 [5]
Упр. 18, 19, 20, 21, 22, 23, стр 38-43 [4]
ТЕСТЫ
1. По какой формуле можно определить выборочную ковариацию:
а) Cov (x, y) =  б) Cov (x, y) =
б) Cov (x, y) = 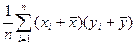
в) Cov (x, y) =  г) Cov (x, y) =
г) Cov (x, y) = 
2. Вычислить 99% доверительный интервал, если при оценивании регрессии между расходами на питание и доходами величина b составляет 0,093, Cov (x, y) = 0,003, tкрит = 2,845 на 1% уровне значимости.
а) 0,084 <  <0,156; б) 0,001 <
<0,156; б) 0,001 <  <0,156; в) 0,084 <
<0,156; в) 0,084 <  <0,101; г) 0,084 <
<0,101; г) 0,084 <  <0,2;
<0,2;
3. Распределение Стьюдента применяется:
а) для нахождения интервальных оценок, а также при проверке статистических гипотез, при этом активно используется таблица критических точек Стьюдента;
б) при проверке статистических гипотез, в дисперсионном и регрессионном анализе, при этом активно используется таблица критических точек Стьюдента;
в) для нахождения интервальных оценок, а также при проверке статистических гипотез, при этом активно используется таблица критических точек  - распределения;
- распределения;
г) при проверке различных гипотез в статистике (о величине математического ожидания при известной дисперсии, о равенстве математических ожиданий).
4. Если эконометрическая модель содержит только одну объясняющую переменную, она называется:
а) линейной регрессией; б) парной регрессией; в) множественной регрессией; г) моделью временного ряда.
5. В случае, если выборка имеет 25 наблюдений, то при парной линейной регрессии число степеней свободы t – распределения Стьюдента составит:
а) 23; б) 25; в) 27; г) 21.
6. Имеются данные о связи между стоимостью основных производственных фондов и объемов валовой продукции по трем однотипным предприятиям (см.табл)
| Основные производственные фонды (х) В млн. тенге | Валовая продукция (y) в млн. тенге |
Используя МНК, найдите неизвестные параметры в стандартном уравнении вида y =  +bx
+bx
а)  ; б)
; б)  ;в)
;в) 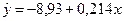 ; г)
; г)  ;
;
7. В некоторой стране годовой доход каждого индивида y определяется по формуле: 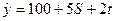 , где S - число лет обучения индивида, t -трудовой стаж (в годах), x - возраст индивида. Рассчитайте cov(x,t) для выборки из 4-х индивидов, описанных ниже:
, где S - число лет обучения индивида, t -трудовой стаж (в годах), x - возраст индивида. Рассчитайте cov(x,t) для выборки из 4-х индивидов, описанных ниже:
| Индивид | Возраст(годы) | Годы обучения | Трудовой стаж | Доход |
а) 25,5 б) 26 в) 26,5 г) 32,7
8 Дайте экономическую интерпретацию параметрам уравнения  , где у – объем валовой продукции, х – стоимость основных производственных фондов:
, где у – объем валовой продукции, х – стоимость основных производственных фондов:
а) с увеличением стоимости основных производственных фондов на один млн. тенге объем валовой продукции увеличится на 0,43%;
б) с увеличением объема валовой продукции на 1 млн. тенге стоимость основных фондов увеличивается в 0,43 млн. тенге;
в) с увеличением стоимости основных производственных фондов на 1% объем валовой продукции уменьшается на 0,43 млн. тенге;
г) с увеличением стоимости основных производственных фондов на один млн. тенге объем валовой продукции уменьшается в среднем на 0,43млн. тенге.
9. Что значит проверить значимость уравнения регрессии:
а) проверить, соответствует ли построенная модель моделируемому реальному экономическому объекту или процессу;
б) оценить тесноту корреляционной зависимости;
в) проверить, соответствует ли математическая модель экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных;
г) выразить в математической форме обнаруженные связи и соотношения.






