Основные понятия: нормализованное представление вещественных чисел, выравнивание порядков, нормализованный результат.
Условные обозначения:
 - задания до чтения текста
|  - задания во время чтения
|  - задания после чтения
|
|
| Прочитайте текст. Во время чтения делайте пометки на полях, выделяя главное. |
К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ.
Сложение и вычитание
При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков.
В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу.
В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются.
В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.
Пример 1. Сложить двоичные нормализованные числа 0,10111•2–1 и 0,11011*210. Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо:
Пример 2. Выполнить вычитание двоичных нормализованных чисел 0,10101*210 и 0,11101*21. Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:
Результат получился не нормализованным, поэтому его мантисса сдвигается влево на два разряда с соответствующим уменьшением порядка на две единицы: 0,1101*20.
Умножение
При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются.
Пример 3. Выполнить умножение двоичных нормализованных чисел:
(0,11101•2101) • (0,1001•211) = (0,11101•0,1001) • 2(101+11) = 0,100000101•21000.
Деление
При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется.
Пример 4. Выполнить деление двоичных нормализованных чисел:
0,1111•2100: 0,101•211 = (0,1111: 0,101) • 2(100–11) = 1,1•21 = 0,11•210.
Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического устройства.
|
|
|
|
| Выполните действия, используя правила выполнения арифметических действий над вещественными числами: а) 0,10101•2–11 + 0,01011•210; б) 0,11101•2101 и 0,01101•211; в) (0,10101•2100)*(0,0011•210) г) (0,1101•2111): (0,111•21). |
Модуль 5.
Алгебра логики
Тема 5.1 Основные понятия алгебры логики.
Основные понятия: алгебра логики, высказывание, логическая переменная, логическая функция.
Условные обозначения:
| - задания до чтения текста
| - задания во время чтения
| - задания после чтения
|
|
| По указанным ключевым словам составьте мини-рассказ из трех-четырех предложений. Ключевые слова: алгебра, высказывание, вычисление, истина, формула. |
|
| Прочитайте текст. Во время чтения текста составьте глоссарий (словарь) новых терминов, встречающихся в тексте. |
Математическая логика - это современная форма логики, которая полностью опирается на формальные математические методы. Частью математической логики является алгебра логики - раздел, изучающий строение сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Алгебру логики иногда называют алгеброй Буля, или булевой алгеброй, по имени ее создателя - Джоржа Буля - английского математика (кстати, отца Этель Л. Войнич, написавшей "Овод"). Основные результаты теории были сформулированы им в книге "Исследование законов мышления", изданной в 1854 году. Во введении Буль писал, что назначение трактата - исследовать основные законы тех операций ума, посредством которых производится рассуждение, выразить их на символическом языке некоторого исчисления и на этой основе установить науку логику и построить ее метод.
Основным объектом изучения математической логики являются элементарные высказывания. Под термином "высказывание" мы будем понимать повествовательное предложение. При этом нас будет интересовать не построение: подлежащее - сказуемое - дополнение, а характерные свойства рассматриваемых образований: являются они истинными или ложными. Высказывания отличаются от других языковых образований тем, что мы можем присвоить им определенное значение истинности - " истина ", если они истинны, значение " ложь ", если они ложны. При этом мы исходим из "принципа исключенного третьего", или "третьего не дано", который состоит в том, что каждое высказывание или истинно, или ложно, и других возможностей нет. Ситуация, когда ни истинно, ни ложно, была бы и в обычном смысле неразрешимой. Этот принцип называют принципом двузначности.
Все научные знания (законы и явления физики, химии и биологии, математические теоремы и т.д.), события повседневной жизни, ситуации, возникающие в процессах управления, формулируются в виде высказываний.
Примеры высказываний:
" 35 делится на 7 ",
"Москва - столица России".
Все они имеют значение истинности " истина ".
Следующие высказывания имеют значение истинности " ложь ":
" Мышь больше слона ",
" Молодые лошади называются щенятами ",
" 6 больше 8 ".
Повелительные (" Войдите, пожалуйста! "), вопросительные (" Знаешь ли ты информатику? ") и бессмысленные предложения не являются высказываниями.
Если логика имеет дело со смыслом высказываний, то в алгебре логики работают с формулами. Любое элементарное высказывание обозначается малой буквой латинского алфавита (в нашем повествовании - х i), совершенно так же, как в элементарной алгебре обозначаются величины, когда мы абстрагируемся от того, какие именно предметы изучаются, нас интересует только их количество и соотношение между ними.
Поскольку высказывание может принимать одно из двух значений, то говорят о "переменных высказываниях". Это означает, что рассматривается не только конкретно определенное высказывание хi , но также некоторая логическая переменная х i , которую можно использовать для обозначения произвольного высказывания. Замещение переменной конкретным высказыванием означает предоставления одного из значений " истина " или " ложь ".
Итак, в алгебре логики в каждом высказывании мы будем отвлекаться от всех особенностей высказывания, кроме одного - истинно оно или ложно. Истинное высказывание условно обозначается единицей (если x1 - высказывание " 35 делится на 7 ", то x1 = 1), а ложное - нулем (если x2 - высказывание " мышь больше слона ", то x2 = 0).
Таким образом, диапазон изменения переменного - xi в алгебре логики существенно меньше, чем изменение переменного в элементарной алгебре: оно принимает только одно из двух значений - или 1, или 0.
Из элементарных высказываний с помощью логических связок " и ", " или ", " не ", " если -то " и других (логических операций) строятся сложные высказывания - формулы (или функции) алгебры логики.
Способы построения новых высказываний из заданных с помощью логических связок, их преобразования и установления истинности изучаются в логике высказываний с помощью алгебраических методов.
Сущность алгебраического подхода к логике поясним на примере элементарной алгебры - алгебры арифметики. Основные объекты алгебры арифметики - выражения (формулы), состоящие из букв, знаков операций и скобок. С формулами производят процедуры двух типов: вычисления и преобразования.
Вычисления - вместо букв подставляют числа, знаки указывают действия, а скобки их порядок. Каждая формула задает функцию. Переменные - буквы формулы.
Преобразование формулы происходит так: исходная формула или ее часть F1 заменяется другой, в результате получается новая формула F2, которая эквивалентна F1 (т.е. при любых значениях аргументов F1 и F2 дают один и тот же результат). Преобразование выражений производится на основе законов арифметики, а также полученных из них соотношений типа (a + b) 2 = a 2 + 2ab + b 2 и т.п.
По аналогии строится алгебра логики. Она рассматривает логические выражения как алгебраические, которые можно преобразовать по определенным правилам. Разница заключается в том, что в выражениях алгебры логики переменные являются логическими (0 и 1). Знаки операций обозначают логические операции (логические связки).
В логических задачах исходными данными являются суждения, подчас неожиданные и нередко весьма запутанные. Высказывания и связи между ними бывают иногда столь противоречивыми, что такие "твердые орешки" не под силу "раскусить" и вдумчивому математику.
В данных случаях большую помощь может оказать ЭВМ как необходимый инструмент эффективного решения логических задач с многими переменными. В настоящее время нет ни одного языка программирования, который не включал бы логических операций.
|
| Выделите из новых терминов ключевые. Сравните содержание мини-рассказа по ключевым словам, который Вы составили вначале работы, с интерпретацией этих понятий в тексте лекции. Заполните таблицу:
|
|
| Ответьте письменно на вопросы и выполните задания: 1) Являются ли высказываниями следующие предложения: а) Все студенты получают стипендию. б) Сегодня на улице хорошая погода. в) 2>5. г) Как вы себя чувствуете? д) Бегемоты летают очень низко. е) Который час? ж) 2х + 5 = 9. 2) Определите значение истинности следующих простых высказываний: а) А = Урок длится 45 минут; б) В = Процессор является устройством обработки информации; в) С = Переименуй данный файл; г) D = Оперативная память является устройством кодирования информации; д) E = Что такое сканер? 3) Приведите примеры истинных простых высказываний (три примера). 4) Приведите примеры ложных простых высказываний (три примера). 5) Приведите примеры предложений, которые не являются высказываниями (три примера). |
Тема 5.2 Основные логические операции.
Основные понятия: логические операции, инверсия, конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, эквиваленция (эквивалентность).
Условные обозначения:
| - задания до чтения текста
| - задания во время чтения
| - задания после чтения
|
|
| Прочитайте текст. Во время чтения текста составьте таблицу:
|
В алгебре логики основными (элементарными) операциями являются отрицание, логическое сложение (дизъюнкция), логическоеумножение (конъюнкция), импликация, эквивалентность.
Отрицание. Операция отрицания соответствует в обычном языке частице не. Функция, получающаяся в результате применения операции отрицания к высказыванию x, обозначается так: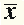 
. Читается " не икс ". Заметим, что в математической логике до сих пор нет единых обозначений, поэтому вместо 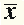можно встретить и другие обозначения, смысл которых тот же самый, например, 
или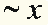 
.
Новое сложное высказывание 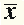- ложно при условии, что высказывание x истинно и истинно при условии, что x - ложно. Запишем эти зависимости в виде таблицы истинности (формальное определение дадим позднее) для операции отрицания:
| x |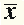
|
Пример 1. Обозначим суждение (высказывание) " Я иду в кино " через x 1, а суждение " Я достаю билеты в театр " через x 2. Тогда в сложном суждении " Если я завтра достаю билеты в театр, то не иду в кино (x 2 = 1, x 1 = 0), а если я не достану билеты в театр, то пойду в кино (x 2 = 0, x 1 = 1)" высказывания x 1 и x 2 связаны между собой операцией отрицания: x 1 = .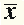
Логическое умножение (конъюнкция). Обозначается x1  x 2 Другие обозначения: x 1 x 2, x 1 & x 2. Читается " икс один и икс два ". Это сложное суждение, которое истинно только в том случае, когда и суждение x1, и суждение x 2 истинны. В остальных случаях сложное высказывание ложно.
Таблица истинности для конъюнкции (логического умножения):
Пример 2. Рассмотрим условия, необходимые для получения человеком водительских прав. Суждение " Человек получает права водителя " обозначим через y. Для получения прав необходимо получить положительное заключение медицинской комиссии о состоянии здоровья. Сформулируем высказывание " Человек здоров " и обозначим его x1. Кроме здоровья, надо еще сдать два экзамена: по вождению и по правилам дорожного движения (ПДД). Высказывания: x 2 - " Экзамен по вождению сдан успешно "; x 3 - " Экзамен по ПДД сдан успешно ". В символической записи имеем: y = x 1 Суждение y будет истинным (y = 1) только в том случае, если истинны все три суждения: x 1 = 1, x 2 = 1 и x 3 = 1. При всех других комбинациях y = 0, то есть высказывание y ложно: человек не получит прав водителя. Логическое сложение (дизъюнкция). Обозначается x 1 Логическое сложение выражает суждение (сложное высказывание), которое истинно в том случае, если хотя бы одно из суждений истинно. Таблица истинности логического сложения: | |||||||||||||||
Пример 3. Боря давно хотел иметь книгу "Основы информатики и вычислительной техники", где рассматриваются вопросы алгебры логики. Он попросил своих товарищей Андрея и Валерия, чтобы они обязательно купили для него эту книгу, если она им попадется. У Бориса будет книга (суждение y) при выполнении равенства: y =x 1 где x 1 - высказывание " Андрей купил книгу ", x 2 - высказывание " Валерий купил книгу ". Высказывание y =x 1 |
x 2. Читается " икс один или икс два ". Знак " Импликация (следование). Обозначается x 1 
x 2. Логически реализует связку естественной речи " если …, то… ". Импликация определяется следующим образом:
| x 1 | x 2 | x 1 x 2
|
Например, в профессиональной речи следователь часто логически рассуждает примерно так: "Если кража произошла до полуночи, то наверняка это совершил Вольдемар". Нетрудно заметить, что два высказывания: x 1 -" Кража произошла до полуночи "и x 2 -" Вор - Вольдемар " связаны операцией импликации x 1 x 2
Данное умозаключение будет истинным, если при истинном x 1 истинно x 2. Логическое выражение будет ложным, если при истинном x 1 оказывается ложным x 2.
Замечание. Если x 1 = 0 (высказывание - предположение ложно, или, говорят, ложная посылка), то x 2 (следствие) может быть как истинным (" Вор - Вольдемар ", x 2 =1), так и ложным (" Вор - не Вольдемар ", x 2 = 0). Но логического смысла выражение не имеет. Данное положение вещей выражается с помощью поговорки " ex falso guod libet ", или " из ложной посылки можно вывести всякое ".
В обычной речи такие высказывания не имеют значения, поскольку выражения типа " Если кто-то сумасшедший, то 5 меньше 2 " рассматриваются как бессмысленные. Это связано с тем, что в обычной речи предусматривается содержательная связь, причинные отношения между посылкой (причиной) x 1 и заключением (следствием) x 2, которые здесь не заданы. Такая содержательная связь не может быть описана с помощью логики высказываний.
Эквиваленция (равносильность). Эквиваленцией (или эквивалентностью) двух высказываний x 1 и x 2 называется новое высказывание, которое считается истинным, когда оба высказывания x 1 и x 2 либо одновременно истинны, либо одновременно ложны, и ложным - во всех остальных случаях.
Эквиваленция высказываний x 1 и x 2 обозначается символом x 1 
x 2 (или x 1 = x 2, или x 1 
x 2), читается " для того, чтобы x 1, необходимо и достаточно, чтобы x 2 " или " x 1 тогда и только тогда, когда x 2 ". Высказывания x 1 и x 2 называются членами эквивалентности.
Логические значения операции эквивалентности описываются следующей таблицей истинности.
| x 1 | x 2 | x 1 x 2
|
Например, эквиваленция " Треугольник SPQ с вершиной S и основанием PQ равнобедренный тогда и только тогда, когда угол P равен углу Q " является истинной, так как высказывания " Треугольник SPQ с вершиной S и основанием PQ равнобедренный " и " В треугольнике SPQ с вершиной S и основанием PQ угол P равен углу Q " либо одновременно истинны, либо одновременно ложны.
Эквиваленция играет важную роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквиваленции. В этом случае, зная об истинности или ложности одного из двух членов эквиваленции и доказав истинность самой эквиваленции, мы заключаем об истинности или ложности второго члена эквиваленции.
Итак, мы дали определения элементарных логических операций. Они позволяют строить сложные (составные) высказывания на основе заданных высказываний.
Пусть x 1, x 2, x 3, x 4 - переменные высказывания (логические переменные), тогда следующие высказывания:
представляют формулы алгебры высказываний.
Так же, как и в алгебре арифметики, в алгебре логики устанавливается приоритет выполнения логических операций. Они упорядочены в следующей последовательности:
При этом отрицание является наиболее сильной операцией, эквивалентность - самой слабой. С учетом указанного порядка две формулы:
и
имеют одинаковые значения.
Истинность составных высказываний (логических формул), образованных в результате выполнения логических операций над простыми высказываниями, зависит от истинности исходных высказываний.
|
| 1. Сформулируйте мнемонические правила (правила для запоминания) построения таблиц истинности для инверсии, конъюнкции, дизъюнкции, импликации, эквиваленции.
2. Приведите примеры сложных высказываний, образованных из двух простых инверсией. Запишите это высказывание формулой.
3. Приведите примеры сложных высказываний, образованных из двух простых конъюнкцией. Запишите это высказывание формулой.
4. Приведите примеры сложных высказываний, образованных из двух простых дизъюнкцией. Запишите это высказывание формулой.
5. Приведите примеры сложных высказываний, образованных из двух простых импликацией. Запишите это высказывание формулой.
6. Приведите примеры сложных высказываний, образованных из двух простых эквиваленцией. Запишите это высказывание формулой.
7. Приведите примеры сложных высказываний, образованных из трех простых конъюнкцией и дизъюнкцией. Запишите это высказывание формулой.
8. Приведите примеры сложных высказываний, образованных из трех простых конъюнкцией и импликацией. Запишите это высказывание формулой.
9. Логическими переменными A, B, C, D, E обозначены следующие простые высказывания: A – яблоко красное, B – яблоко вкусное, C – яблоко сладкое, D – яблоко крупное, E – яблоко твердое. Записать формулой сложное высказывание: "яблоко вкусное, хотя зеленое, но и не кислое".
10. Логическими переменными A, B, C, D, E обозначены следующие простые высказывания: A – яблоко красное, B – яблоко вкусное, C – яблоко сладкое, D – яблоко крупное, E – яблоко твердое. Записать формулой сложное высказывание: "красный цвет яблока необходим и достаточен для того, чтобы оно было вкусное и одновременно мягкое"
11. Логическими переменными A, B, C, D, E обозначены следующие простые высказывания: A – яблоко красное, B – яблоко вкусное, C – яблоко сладкое, D – яблоко крупное, E – яблоко твердое. Записать формулой сложное высказывание: "яблоко вкусное, хотя зеленое, но и не кислое"
12. Логическими переменными A, B, C, D, E обозначены следующие простые высказывания: A – яблоко красное, B – яблоко вкусное, C – яблоко сладкое, D – яблоко крупное, E – яблоко твердое. Записать формулой сложное высказывание: "неверно, что если яблоко зеленое, то оно или твердое или кислое"
13. Придумайте сложное высказывание, которое можно записать формулой:
а)  ;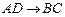
б)  .
|
Тема 5.3. Упрощение логических выражений с использованием законов алгебры логики
Основные понятия: логические выражения, тождественные преобразования логических выражений, законы алгебры логики.
Условные обозначения:
| - задания до чтения текста
| - задания во время чтения
| - задания после чтения
|
|
| Прочитайте текст. Сделайте конспект. |
В алгебре логики выполняются некоторые законы, позволяющие производить тождественные преобразования логических выражений. Эти законы сведены в таблицу 6.1.
Таблица 6.1
| Закон | Для «ИЛИ» | Для «И» |
| Переместительный | 
| 
|
| Сочетательный | 
| 
|
| Распределительный |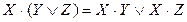 
| 
|
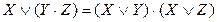
| Правила де Моргана | 
| 
|
| Идемпотенции | 
| 
|
| Поглощения | 
| 
|
| Склеивания |  
| 
|
| Операция переменной с ее инверсией | 
| 
|
| Операция с константами | 
| 
|
| Двойного отрицания | 
|
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0, 0), (0, 1), (1, 0), (1, 1).
Если формула содержит три переменные, то возможных наборов значений переменных восемь: (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Задача 6.1. Выяснить, является ли формула 
тождественно истинной.
Решение
Составим таблицу истинности для формулы , которая содержит две переменные X и Y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу 6.2. Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.
Таблица 6.2
| Переменные | Промежуточные логические формулы | Формула | |||||
| x | y | 
| 
| 
| 
| 
| 
|
Задача 6.2. Выяснить, является ли формула 
тождественно ложной.
Решение
Таблица истинности для формулы показана в таблице 6.3. Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.
Таблица 6.3
| Переменные | Промежуточные логические формулы | Формула | ||||
| x | y | 
| 
| 
| 
| 
|
Задача 6.3. Является ли выполнимой формула 
?
Решение
Таблица истинности для формулы показана в таблице 6.4.
Таблица 6.4
| Переменные | Промежуточные логические формулы | Формула | ||||||
| x | y | z |
| 
| 
|
| 
|
|
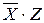
Из таблицы видно, что формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Под упрощением формулы понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций либо содержит меньшее число вхождений переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1) 
(законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами);
2) 
(применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией);
3) 
(повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания);
4) 
(сначаладобиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания);
Из этих примеров видно, что при упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином шаге.
|
| Ответьте письменно на вопросы и решите задачи:
1. Сформулируйте основные законы алгебры логики.
2. Составить таблицы истинности логических формул:
3. Упростить логические формулы: а) б) в) 4. Упростите логическое выражение. Упрощенный вид должен содержать одну логическую операцию
5. Является ли тождественно истинным данное выражение?
|
;
;
.
Тема 5.4 Упрощение логических выражений с использованием совершенных форм
Основные понятия: совершенные нормальные формы, совершенная конъюнктивная нормальная форма (СКНФ), совершенная дизъюнктивная нормальная форма (СДНФ).
Условные обозначения:
| - задания до чтения текста
| - задания во время чтения
| - задания после чтения
|
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Например,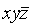 
является простой конъюнкцией,
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение 
является ДНФ.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке.
Например, выражение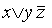 
является ДНФ, но не СДНФ. Выражение 
является СДНФ.
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение 
– простая дизъюнкция,
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение 
– КНФ).
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение 
является СКНФ.
Пример нахождения СДНФ
Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. Пусть дана некоторая функция f(x1, x2, x3, x4),заданная своей таблицей истинности:
Таблица 1
| 
| 
| 
| 
|
В ячейках результата отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.
Первая строка содержит 1 в указанном поле. Отмечаются значения всех четырёх переменных, это:
· 
· 
· 
· 
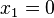
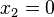
Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так: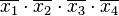 
Переменные второго члена:
·
·
·
· 
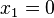
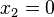
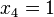
в этом случае будет представлен без инверсии: 
Таким образом анализируются все ячейки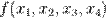 
. Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).
СДНФ этой функции:
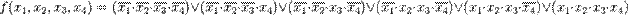
Пример нахождения СКНФ
Для того, чтобы получить СКНФ функции, требуется составить её таблицу истинности (Таблица1).
В ячейках строки́ отмечаются лишь те комбинации, которые приводят логическое выражение в состояние нуля.
Четвёртая строка содержит 0 в указанном поле. Отмечаются значения всех четырёх переменных, это:
·
·
· 
·
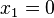
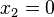
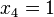
В дизъюнкцию записывается переменная без инверсии, если она в наборе равна 0, и с инверсией, если она равна 1. Первый член СКНФ рассматриваемой функции выглядит так: 
Остальные члены СКНФ составляются по аналогии.
