Функции F на границах
| № шага | Значения границ | Значения функции F ([O]) | ||||
| [O]1 | [O] | [O]2 | F ([O]1) | F ([O]) | F ([O]2) | |
| 1. | 5·10-4 | 3·10-4 | 1·10-4 | – 6,76·10-1 | – 1,41·10-2 | 1,41 |
| 2. | 3·10-4 | 2·10-4 | 1·10-4 | – 1,41·10-1 | 5,13·10-1 | 1,41 |
| 3. | 3·10-4 | 2,5·10-4 | 2·10-4 | – 1,41·10-1 | 2,23·10-1 | 5,13·10-1 |
| 4. | 3·10-4 | 2,75·10-4 | 2,5·10-4 | – 1,41·10-1 | 1,0·10-1 | 2,23·10-1 |
| 5. | 3·10-4 | 2,88·10-4 | 2,75·10-4 | – 1,41·10-1 | 3,89·10-2 | 1,0·10-1 |
| 6. | 3·10-4 | 2,94·10-4 | 2,88·10-4 | – 1,41·10-1 | 1,21·10-2 | 3,89·10-2 |
| 7. | 3·10-4 | 2,97·10-4 | 2,94·10-4 | – 1,41·10-1 | – 1,06·10-3 | 1,21·10-2 |
| 8. | 2,97·10-4 | 2,96·10-4 | 2,94·10-4 | – 1,06·10-3 | 3,31·10-3 | 2,94·10-4 |
| 9. | 2,97·10-4 | 2,965·10-4 | 2,96·10-4 | – 1,06·10-3 | 1,126·10-3 | 3,31·10-3 |
| 10. | 2,97·10-4 | 2,9675·10-4 | 2,965·10-4 | – 1,06·10-3 | 3,1·10-5 | 1,126·10-3 |
| 11. | 2,97·10-4 | 2,9687·10-4 | 2,9675·10-4 | – 1,06·10-3 | – 4,951·10-4 | 3,1·10-5 |
Для ускорения поиска ошибок, проверку необходимо выполнить студенту, у которого такой же раскислитель.
Как следует из табл. 1, в качестве границ начального отрезка (шаг 1 в таблице) приняты [O]1 = 5 ·10-4 и [O]2 = 1 ·10-4. Деление отрезка пополам дает значение [O] = 3 ·10-4.
На границах отрезка значения функции имеют различные знаки F ([O]1) = -6,76 ·10-1 и F ([O]2) = 1,41, поэтому находим середину отрезка (операция 1) [O] = 3 ·10-4 и подсчитываем F ([O]) = – 1,41·10-2 (операция 2). Далее рассматриваем новый отрезок [3·10-4, 1·10-4] (операция 3), на границах которого функция принимает различные знаки (-1,41·10-2, 1,41). Затем операции (1-3) продолжаются на каждом шаге таблицы.
Итак, корень уравнения (30) находится на отрезке [2,9675·10-4, 2,9687·10-4], на границах которого функци я F принимает значения различных знаков (-4,951·10-4 и 3,1·10-5). Оценим погрешность определения точного значения корня:
Итак, погрешность находиться в пределах заданной.
Учитывая, что 
ближе к 0, чем 
, принимает в качестве корня значение 
.
Для тестирования программы сравниваем [O]* и 
и оцениваем относительную величину отличия полученного методом половинного деления решения [O]* от программного :
.
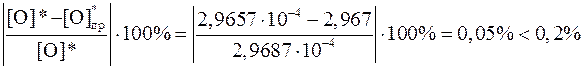Итак, отличие решений несущественное и программа готова к расчетам.
Далее согласно заданию работы 1.4 в п.1 при 
необходимо варьировать концентрацию раскислителя для различных значений активности оксида раскилителя и находить по программе расчета концентрации кислорода, равновесной с раскислителем. Результаты расчета заносят в табл. 2.
Таблица 2
Результаты расчета концентрации кислорода [O]·104, равновесной с раскислителем Al, при варьировании концентрации Al для различных значений активности оксида Al2O3 и 
| [Al], % | Активность оксида Al2O3 | ||
| 0,1 | 0,5 | 1,0 | |
| 0,1 | 2,017 | 3,454 | 4,356 |
| 0,11 | 2,07 | 3,544 | 4,47 |
| 0,12 | 2,136 | 3,657 | 4,613 |
| 0,13 | 2,214 | 3,792 | 4,782 |
| 0,14 | 1,872 | 3,947 | 4,978 |
| 0,15 | 2,406 | 4,124 | 5,200 |
| 0,16 | 2,52 | 4,318 | 5,447 |
Результаты расчета в графическом виде представлены на рис. 1 в виде зависимостей концентрации кислорода от концентрации раскислителя для различных значений активности оксида Al2O3.
Далее согласно заданию 1.5 проводим расчеты по программе расчета концентрации кислорода [O], равновесных с раскислителем Al, при различных значениях температуры для различных значений активности оксида Al2O3 и [Al] = 0,13 %. Результаты расчета концентрации кислорода [O]·104 заносят в табл. 3.
На рис. 2 результаты расчета (табл. 2) представлены в виде зависимостей концентрации кислорода, равновесного с раскислителем Al, от температуры для различных значений активности оксида Al2O3 при [Al] = 0,13 %.
 |
В заключении работы выполняются пункты 1.6 и 1.7 задания.
Рис. 1. Зависимость концентрации кислорода
от концентрации раскислителя для различных значений
активности оксида Al2O3
Таблица 3
| Т, °С | Активность оксида Al2O3 | ||
| 0,1 | 0,5 | 1,0 | |
| 1,528 | 2,616 | 3,298 | |
| 1,732 | 2,964 | 3,738 | |
| 1,960 | 3,355 | 4,231 | |
| 2,214 | 3,792 | 4,782 | |
| 2,498 | 4,280 | 5,399 | |
| 2,816 | 4,825 | 6,088 | |
| 3,170 | 5,434 | 6,856 |
Рис. 2. Зависимость концентрации кислорода, равновесного
с раскислителем Al, от температуры для различных значений
активности оксида Al2O3 при [Al] = 0,13 %.
Приложение 1
Справочные таблицы
Таблица П.1.1 – Стандартная энергия Гиббса образования оксидов
из элементов (D G = A + BT Дж/моль) при температурах
сталеплавильных процессов (1800 – 2000 К)
| Реакция | А | В |
| -1681000 | 324,08 |
| -118000 | -83,77 |
| -397000 | 0,2 |
| -408400 | |
| -947000 | |
| -936000 | |
| -1131000 |
Таблица П.1.2 – Термодинамические данные реакций
