Методика изложена на примере раскисления стали алюминием.
Для определения константы равновесия реакции раскисления необходимо составить схему реакции таким образом, чтобы элемент-раскислитель и кислород были в растворенном состоянии [5]. В качестве примера рассмотрим реакцию раскисления стали алюминием:
.
Расчет, lgK и К реакции раскисления стали
Алюминием
Используя данные работы [1] и табл. П.1.1-П.1.2, составим следующую схему расчета для реакции раскисления стали:
1. Образование оксида Al2O3 из исходных веществ, находящихся в термодинамически устойчивом при данной температуре состоянии:
(1) 
; 
Дж/моль. (16)
2. Растворение алюминия в расплаве металла:
(2) 
; 
Дж/моль.
3. Растворение кислорода в расплаве металла
(3) 
; 
Дж/моль.
Тогда величину 
исходной реакции можно вычислить комбинируя уравнения реакций (1)-(3):
Дж/моль (18)
По формуле (14) находим температурную функцию константы равновесия реакции раскисления металла алюминием
lgК = 62890/ T – 19,85. (19)
Для температуры 1873К вычисляем константу равновесия реакции
lgК = 13,73.
Сравним полученные значения константы равновесия реакции с литературными данными.
Для реакции раскисления металла алюминием
2/3[Al](1 %) +[O] (1 %) = 1/3 (Al2O3)тв
в работе [2] получено уравнение:
, Дж/моль. (20)
Приведенная реакция отличается от рассматриваемой в примере стехиометрическими коэффициентами.
После приведения в соответствие указанных коэффициентов и внесения поправок – уравнение (20) принимает следующий вид:
, Дж/моль. (21)
Откуда получим
lgК = 64160/ T – 20,36. (22)
При температуре 1873К имеем
lgК = 13,89.
Таким образом, вычисленное значение логарифма константы равновесия реакции показывает достаточно хорошую сходимость с найденным в нашем примере. Далее выведем уравнение типа (16) для определения равновесных концентраций кислорода в стали известного состава.
Расчет равновесных концентраций кислорода в металле,
Раскисленном алюминием
Исходные данные для расчета (задаются вариантом).
Состав металла, % по массе: 0,45C; 0,17Si; 1,0Mn; 0,10-0,16Al; 0,04P; 0,03S.
Температура, °С: 1560-1620.
Из Приложения табл. П.1.3 выбираем термодинамические массовые параметры взаимодействия первого порядка элементов 
.
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
;
; 
.
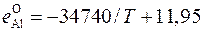Запишем константу равновесия реакции раскисления металла алюминием
. (23)
В результате логарифмирования уравнение (23) можно записать:
. (24)
Последовательно выражая общие коэффициенты активности f Al и f O через частные и термодинамические массовые параметры взаимодействия первого порядка элементов, получим выражения для расчета lg f Al и lg f O:
, (25)
, (26)
, (27)
, (28)
После подстановки (27) и (28) в уравнение (24) и несложных преобразований получим уравнение изотермы раскисления в общем виде:
(29)
Для определения равновесной концентрации кислорода [O] необходимо решить уравнение (29). Однако, уравнение (29) является трансцендентным относительно [O], поэтому оно решается с помощью пакета Matcad-2000, установленного на компьютерах в аудитории 27б. Для этого составляется программа на языке Matcad. Пример программы для решения уравнения (24), которое имеет более общий вид по сравнению с уравнением (29), приведен ниже. В начале программы указаны исходные данные по концентрации раскислителя (Al, %), температуре (Т, °К) и активности оксида раскислителя (
), затем термодинамические массовые параметры взаимодействия первого порядка элементов и выражение для функции f, которой обозначена левая часть уравнения (24). Последний оператор 100 t (а, b) определяет корень уравнения F ([O]) = 0. С помощью значений а и b указываются границы интервала, в котором предположительно находится корень уравнения. При написании программы использованы идентификаторы, похожие на обозначения величин в формулах, поэтому программу можно легко преобразовать для расчета равновесной концентрации кислорода в стали другого химического состава и раскислителя, согласно заданному варианту (табл. П.2.1).
Пример программы для расчета концентрации кислорода,
Равновесных с алюминием
Исходные данные (определяются вариантом)
aAl2O3:= 1 Т:= 1560 + 273 Al: = 0,1
Химический состав стали
С: = 0,45 Si:= 0,24 Mn:= 0,68 P:= 0,034 S:= 0,032
 |
Термодинамические параметры взаимодействия первого порядка элементов
Константа равновесия реакции равновесия алюминием
Коэффициенты активности алюминия и кислорода
lgfAl(O):= eAlAl(T)·Al + eAlC·C + eAlO(T)·O + eAlSi·Si +
+ eAlMn·Mn + eAlP·P + eAlS·S
lgfO(O):= eOAl(T)·Al + eOC·C + eOO(T)·O + eOSi·Si +
+ eOMn·Mn + eOP·P + eOS·S
Уравнение изотермы раскисления алюминием
f(O):= log(aAl2O3,10) - 2·lgfAl(O) - 2·log(Al,10) –
- 3·lgfO(O) – 3log(O,10) – lgK(T)
Определение равновесной концентрации кислорода
root(f(O),O,10-8,0,1) = 2,851·10-4.
После ввода исходных данных для соответствующего варианта задания производится запуск расчета после подвода курсора к последнему оператору и щелчка левой кнопки «мышки». Для исходных данных =1, Т = 1833°К и [Al] = 0,1 получим [O]пр = 2,967·10-4. К сожалению, пакет Matcad выдает только три цифры после запятой.
После получения первого результаты по активности кислорода в правой части последнего оператора необходимо выполнить тестирование программы, путем сравнения программного результаты с решением уравнения (20) с помощью калькулятора. Для этого подставим в уравнение (29) значения термодинамических массовых параметров взаимодействия первого порядка элементов и константы равновесия (19). В результате получим:
Подставляя в последнее уравнение концентрации элементов в стали ([C] = 0,45 %, [Si] = 0,17 %, [Mn] = 1,0 %, [P] = 0,04 %, [S] = 0,03 %) получим при Т = 1833°К, [Al] = 0,1 %, = 1 уравнение:
(30)
Обратим внимание, что количество значащих цифр в значениях коэффициентов уравнения (30) должно быть не менее, чем приведено в (30).
Решаем транцендентное уравнение (30), т.е. находим его корень [O]* для которого F ([O])* = 0, методом половинного деления.
Для нахождения корня этим методом назначают отрезок [[O]1, [O]2], на котором находится искомый корень, т.е. [O]1 ≤ [O]*≤ [O]2. Для назначения [O]1 и [O]2 используют данные по раскисленной способности раскислителя, приведенные в П.3. Затем вычисляют F ([O]1) и F ([O]2). Если [O]1 и [O]2 выбраны верно, то F ([O]1) и F ([O]2) имеют разные знаки. Если знаки одинаковы, то длину отрезка увеличивают путем переноса той границы, на котором наблюдается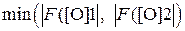 
. Таким образом добиваются условия разных знаков величин F ([O]) на границах
Далее вступает в действие алгоритма половинного деления. Для этого выполняют следующие операции:
1. Определяют новое значение границы по формуле
.
2. Подсчитывают F ([O]).
3. Выбирают отрезок ([O]1;[O]) или ([O];[O]2) в зависимости от того, на границах которого значения функции имеют разные знаки. В результате длина отрезка, на котором находится корень уравнения, сократится в два раза. Далее операции 1-3 повторяют до выполнения условия: 
. В этом случае принимают в качестве корня [O]* = [O]2, которое сравнивают с результатом 
полученным по программе. Если 
, то в программе имеются ошибки, либо некорректен вывод функции F ([O]). Результаты применения метода половинного деления для поиска корня уравнения (30) представлена в табл. 1.
Таблица 1
