Определение грузоподъемности статически. неопределимой шарнирно-стержневой конструкции (задача № 6)

I. Определение грузоподъемности системы расчетом

по упругой стадии деформаций

Найдем степень статической неопределимости системы. В данной конструкции имеем три неизвестные продольные силы в стержнях. Число уравнений статики, которые можно составить для системы сил, сходящихся в одной точке, равно двум. Таким образом, число неизвестных больше числа уравнений равновесия на единицу, и система является один раз статически неопределимой. Можно определить степень статической неопределимости и по-другому. Шарнир (модель которого - точка) для неподвижного закрепления на плоскости требует наложения двух линейных связей. Такими необходимыми связями являются любые два стержня из имеющихся трех стержней системы. Следовательно, оставшийся третий стержень становится лишней кинематической связью (лишним стержнем), а система является один раз статически неопределимой.

Рис. 1.16. План перемещений при расчете по упругой стадии

Для раскрытия статической неопределимости требуется составить уравнения статики, одно (по числу лишних связей) кинематическое соотношение (условие совместности деформаций) и физические уравнения. Рекомендуем начинать решение задачи с записи условия совместности деформаций, построив предполагаемый план перемещений. Для составления уравнений равновесия строим план сил, направления усилий на котором должны быть согласованы с планом перемещений.

1. Уравнение совместности деформаций. Построим предполагаемый план перемещений (рис. 1.16). Величины двух абсолютных деформаций задаем произвольно (например, считаем, что стержни 2 и 3 удлиняются, и откладываем произвольные отрезки и 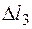вдоль стержней). На пересечении траекторий поворота концов двух стержней (перпендикуляров к направлениям стержней) получаем новое положение шарнира – точку С ¢ на рис. 1.16. Опустив из этой точки перпендикуляр на направление оси стержня 1, найдем величину его абсолютной деформации .

Разложим полное перемещение шарнира – отрезок – на составляющие и . Найдем абсолютные деформации стержней, выразив их через и , используя их геометрическую связь:

,

,

.

Исключив из этих выражений и , получим искомое соотношение между абсолютными деформациями

.

Допускается составлять уравнение совместности деформаций приближенно, измеряя отношения между абсолютными деформациями по построенному в масштабе плану перемещений. Для приближенного определения связи между абсолютными деформациями представим эту связь в виде

.

Неизвестные параметры данной зависимости и определим из двух планов перемещений. При построении первого плана перемещений предположим, что . Измерим деформации первого и третьего стержней. Тогда

.

Построив второй план перемещений в предположении, что , найдем отношение деформаций первого и второго стержней и получим

.

2. Уравнения равновесия. Составим их на основании плана сил. Нарисуем план сил, вырезав узел и заменив отброшенные части стержней внутренними усилиями, причем направления усилий покажем в соответствии с планом перемещений растягивающими (рис. 1.17). Запишем два независимых уравнения статики. Для данной системы таковыми являются:

; ;

; .

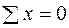Рис. 1.17. План сил в упругой стадии работы

3. Физические соотношения. Поскольку расчет ведется по упругой стадии деформаций, то материал конструкции подчиняется закону Гука (1.3) и для каждого стержня записываем физические уравнения:

; ; .

Полученную систему уравнений решаем относительно усилий , , . Например, при , 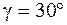это решение имеет вид

, , .

Найденное решение показывает, что усилие в первом стержне отрицательно, т. е. стержень не растянут, как мы предполагали, а сжат. Полученные положительные знаки и подтверждают предположение о том, что эти стержни растянуты.

Для проверки прочности конструкции определим напряжения в стержнях системы:

;

;

.

При расчете по упругой стадии деформации считаем, что предельное состояние конструкции наступит тогда, когда потечет один, наиболее напряженный, стержень. Поскольку пластичный материал имеет одинаковые пределы текучести при сжатии и растяжении, то знак напряжения не имеет значения и первым потечет стержень, в сечении которого возникают наибольшие по модулю напряжения. В данном случае это третий стержень. Из условия его текучести находим предельную нагрузку:

, ;

а из условия прочности - допускаемую нагрузку на конструкцию:

, .

Отметим, что при расчете по упругой стадии деформаций нагрузка и напряжения на всем участке деформирования связаны прямой пропорциональной зависимостью, а потому коэффициенты запаса по напряжениям и по нагрузке равны между собой.

II. Определение предельной грузоподъемности системы

расчетом по упругопластической стадии

Рис. 1.18. Диаграмма Прандтля

Проследим за дальнейшим развитием процесса нагружения – деформирования системы после того, как напряжения в третьем стержне достигли предела текучести. Примем, что материал конструкции работает в соответствии с идеализированной диаграммой упругопластического тела – диаграммой Прандтля (рис. 1.18). При продолжении роста нагрузки напряжения в третьем стержне будут оставаться постоянными и равными . При работе конструкции в упругопластической стадии напряжения в остальных стержнях будут расти в соответствии с упругим законом, но при изменившихся параметрах линейной зависимости от нагрузки. Эти изменения связаны с перераспределением нагрузки только на упругие стержни, обеспечивающие неизменяемость системы в этой стадии ее работы.

Поскольку усилие в стержне 3 уже известно, задача становится статически определимой и усилия в стержнях 1 и 2 находим из уравнений равновесия узла (план сил на рис. 1.19):

; ;

; .

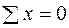Решение этой системы уравнений при , :

, .

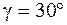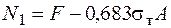Зависимости напряжений от нагрузки на данной стадии работы системы:

, .

Предельное пластическое состояние конструкции достигается тогда, когда напряжения в одном из упругих стержней 1 и 2 достигнут предела текучести и конструкция превратится в механизм. Определим, какой из стержней потечет первым, приравняв напряжения в стержнях пределу текучести и найдя, при каком значении нагрузки стержни потекут:

, ;

, .

Рис. 1.19. План сил в упругопластической стадии работы

Видно, что нагрузка, при которой , меньше и первый стержень потечет раньше второго. Нагрузка, при которой будут течь два стержня (3 и 1), и есть предельная нагрузка для всей конструкции

.

Заметим, что в предельном состоянии напряжения в первом и третьем стержнях достигли предела текучести. При этом первый стержень потек вслед за третьим, хотя к концу упругой стадии напряжения в нем были меньше, чем во втором стержне. Зависимость между напряжениями и нагрузкой с начала деформирования в упругопластической стадии уже не является линейной, а потому одинаковым коэффициентам запаса по нагрузке и по напряжениям в наиболее напряженном упругом стержне будут соответствовать различные значения допускаемой нагрузки. Так, в нашем случае допускаемая нагрузка с коэффициентом запаса по напряжениям определяется из условия

; ; .

Если же исходить из коэффициента запаса 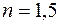по нагрузке, то

; ; .

Очевидно, что расчет по допускаемой нагрузке приводит к повышенному запасу прочности в отдельных стержнях системы, а расчет по допускаемым напряжениям не обеспечивает заданного коэффициента запаса по нагрузке. Поэтому значение допускаемой нагрузки принимаем из условия прочности по нагрузке: .

Следует отметить, что современными строительными нормами проектирования предусматривается раздельное применение коэффициентов надежности по нагрузке и по материалу. Условие прочности в этом случае приняло бы вид

,

где и - коэффициенты надежности (запаса) по нагрузке и по материалу соответственно.

III. Определение предельной грузоподъемности системы

расчетом по предельному пластическому состоянию

Заданная система имеет три деформируемых стержня, один из которых является лишним, так как система один раз статически неопределима. В предельном состоянии, когда конструкция превращается в механизм, должны потечь два стержня (один лишний и один необходимый). В рассмотренных ранее способах решения этой задачи рассматривался порядок перехода материала стержней в пластическую стадию работы, было выяснено, какой стержень потечет первым, какой – вторым. При этом конструкция сначала работает в упругой стадии (материал всех стержней подчиняется закону Гука), затем переходит в упругопластическую стадию работы. Решение вопроса о предельной нагрузке на конструкцию, при которой последняя переходит в механизм, может быть получено и без рассмотрения упругой и упругопластической стадий работы конструкции. Для этого достаточно исследовать равновесие системы в момент перехода в предельное пластическое состояние, т. е. в так называемое предельное равновесие. Сложность состоит в том, что конкретный механизм перехода системы в предельное пластическое состояние заранее неизвестен. Поэтому приходится рассматривать все кинематически возможные варианты перехода к предельному равновесию и для каждого из них вычислять предельную нагрузку. Фактически будет иметь место тот вариант предельного состояния, которому соответствует минимальное значение предельной нагрузки.

В данной задаче возможны три варианта предельного равновесия конструкции: 1) текут стержни 1 и 3; 2) текут стержни 2 и 3 и, наконец, 3) текут стержни 2 и 1.

В качестве примера рассмотрим два варианта предельного пластического состояния в нашей задаче. Согласно первому варианту допустим, что напряжения в стержнях 1 и 3 равны , а стержень 2 работает упруго. Для определения направления усилий в стержнях 1 и 3 построим план перемещений, используя те же правила построения плана перемещений, которые описаны при решении задач № 3 и 5. Поскольку упругие деформации стержня 2 много меньше пластических деформаций стержней 1 и 3, то при построении плана перемещений стержень 2 можно считать абсолютно жестким. Под действием нагрузки жесткий стержень 2 повернется вокруг шарнира А, и этот поворот вызовет укорочение стержня 1 на D l ₁ и удлинение стержня 3 на D l ₃ (рис. 1.20, а). Соответствующий плану перемещений план сил для первого варианта перехода в предельное состояние показан на рис. 1.20, б.

Чтобы неизвестное усилие N ₂ не входило в уравнение, в качестве условия предельного равновесия выберем уравнение "сумма моментов относительно шарнира равна нулю" (см. рис. 1.20, б):

; .

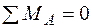Из этого уравнения при 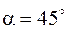, найдем .

Во втором варианте предельного пластического состояния напряжения в стержнях 2 и 3 равны s_т, а первый стержень работает в упругой стадии. Планы сил и перемещений показаны на рис. 1.21. Запишем уравнение предельного равновесия для узла С (такое уравнение равновесие, в которое не входит неизвестное усилие N ₁):

Рис. 1.21. Вариант 2 предельного пластического состояния: а – план перемещений; б – план сил

; .

Отсюда .

Аналогично можно определить предельную нагрузку для третьего варианта, в котором пластически деформироваться будут стержни 1 и 2. Фактической предельной нагрузкой будет минимальное значение из трех полученных. В нашей задаче это (первый вариант предельного состояния), что совпадает со значением, найденным ранее расчетом по упругопластической стадии.

Надо отметить, что число кинематически возможных вариантов предельного состояния может уменьшиться, если ось какого-либо стержня совпадает с линией действия нагрузки (в этом случае поворота этого стержня не происходит и механизма не образуется).

Допускаемое значение нагрузки определяем как отношение предельного значения нагрузки к коэффициенту запаса прочности n.

IV. Определение остаточных напряжений

Процесс нагружения конструкции в упругой и упругопластической стадиях, рассмотренный в пп. I и II, можно отобразить на диаграмме в осях (рис. 1. 22). Характерные точки этой диаграммы получены по соответствующим зависимостям для трех стержней конструкции.

Рассмотрим процесс полной разгрузки системы из положения предельного равновесия (на диаграмме это соответствует вертикальной прямой с абсциссой ). Процесс разгрузки можно трактовать как наложение на существующие напряжения напряжений от отрицательного приращения нагрузки. Закон изменения последних определяется упругим решением задачи до тех пор, пока величина напряжения в одном из стержней не достигнет , поэтому линии разгрузки каждого стержня будут направлены параллельно линиям упругого нагружения (левый участок диаграммы). Если одно из напряжений при разгрузке достигнет величины (как это имеет место в нашем случае), то законы изменения напряжений станут соответствовать упругопластической стадии, а их графики будут параллельны соответствующим линиям нагружения (правый участок диаграммы).

Зависимости можно записать, пользуясь уравнением прямой с известным угловым коэффициентом, проходящей через заданную точку:

,

где - угловой коэффициент прямой линии нагружения, параллельной рассматриваемой линии разгрузки; и - начальные параметры (напряжение и нагрузка в начале участка). В нашем случае , 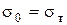для стержней 1 и 3, а для стержня 2 .

Запишем эти зависимости непосредственно после начала разгрузки:

,

,

.

Напряжение , как легко вычислить, достигнет значения при снижении нагрузки до . При этом напряжения в остальных стержнях будут , .

Пользуясь найденными значениями как начальными параметрами, запишем зависимости для напряжений на втором участке разгрузки, проходящей в упругопластической стадии:

,

,

.

При полной разгрузке () получаем следующие значения остаточных напряжений: , , . В заключение следует проверить равновесие узла при полученных значениях остаточных напряжений.