Пусть задано линейно преобразование вида
 , (1)
, (1)
которое вполне определяется матрицей коэффициентов 
(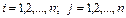 )
)
 .
.
Матрица А называется матрицей линейного преобразования.
Вектор 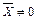 называется собственным вектором линейного преобразования, заданного матрицей А, если найдется такое число λ, что выполняется условие
называется собственным вектором линейного преобразования, заданного матрицей А, если найдется такое число λ, что выполняется условие  .
.
Это число λ называют собственным значением линейного преобразования, соответствующим собственному вектору 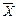 .
.
Каждое собственное значение матрицы А является корнем ее характеристического уравнения
 . (2)
. (2)
Координаты собственных векторов, соответствующих найденным собственным значениям, находят из системы уравнений
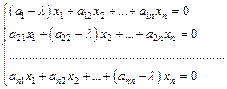 . (3)
. (3)
Пример. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей
 .
. 
Решение. Составляем характеристическое уравнение
 .
.
Раскроем определитель по правилу треугольника

В результате преобразований последнее выражение примет вид:
 .
.
Разложим левую часть уравнения на множители
 ,
,
 ,
,
 .
.
Решением уравнения  будут значения
будут значения  ,
,  , которые являются собственными значениями матрицы А.
, которые являются собственными значениями матрицы А.
Для отыскания координат собственных векторов составим систему уравнений

Найдем собственные векторы, соответствующие значению  .
.
При  получим систему уравнений
получим систему уравнений
 ,
,
или
 .
.
Легко видеть, что ранг матрицы системы равен 1, и система эквивалентна одному уравнению:
 ,
,
откуда
 .
.
Если принять 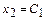 , а
, а  , то значение
, то значение 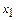 будет равно
будет равно  , где
, где  и
и  - произвольные действительные числа.
- произвольные действительные числа.
Таким образом, все собственные векторы, соответствующие  , определяются равенством
, определяются равенством
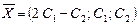 .
.
Найдем собственные векторы, соответствующие 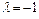 .
.
При 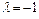 получим систему уравнений
получим систему уравнений
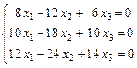
или
 .
.
Запишем матрицу этой системы уравнений
 .
.
Так как определитель этой матрицы равен 0, а минор второго порядка
 ,
,
то ранг матрицы равен двум, и первые два уравнения системы линейно независимы. Оставим в системе только независимые уравнения, члены с  перенесем в правые части уравнений:
перенесем в правые части уравнений:
 .
.
Пусть  , где
, где  - любое действительное число. Тогда система уравнений примет вид:
- любое действительное число. Тогда система уравнений примет вид:
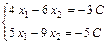 .
.
Решим эту систему методом Гаусса
 ~
~  ,
,
 ,
,
 ,
,  .
.
Таким образом, все собственные векторы, соответствующие 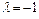 , определяются равенством
, определяются равенством

или
 .
.
Ответ. При собственном значении  собственные векторы равны
собственные векторы равны  . При собственном значении
. При собственном значении 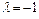 собственные векторы равны
собственные векторы равны  .
.
Задачи для самостоятельного решения
Найти собственные векторы матрицы и соответствующие им собственные значения:
-
 .
. -
 .
. -
 .
.
Ответы: 1)  ,
,  ,
, 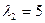 ,
,  ,
,
2)  ,
,  ,
, 


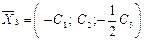 , 3)
, 3)  ,
,  ,
,

 - любой вектор, удовлетворяющий условию
- любой вектор, удовлетворяющий условию  .
.
ОГЛАВЛЕНИЕ
СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Основные понятия и определения
1.2.Методы решения систем линейных уравнений
Метод Крамера
Матричный метод
Метод Гаусса
1.3.Задачи для самостоятельного решения
1.4 Вопросы для подготовки к экзамену
КОМПЛЕКСНЫЕ ЧИСЛА






