AX = B, (5)
где А - основная матрица системы, Х - матрица-столбец неизвестных,
В - матрица-столбец свободных членов
, 
, 
.
Решением матричного уравнения будет матрица Х, которую находят путем умножения обратной матрицы А -1 на матрицу В – столбец свободных членов
Х = А -1 В. (6)
Пример 2. Решить матричным методом систему уравнений
.
Решение. Составим основную матрицу системы А, матрицу – столбец свободных членов В, матрицу – столбец неизвестных Х
, 
, 
.
Найдем обратную матрицу А -1. Для этого вычислим определитель матрицы системы
.
Определитель отличен от нуля, следовательно, систему уравнений можно решать матричным способом.
Далее найдем алгебраические дополнения для всех элементов матрицы по формуле
,
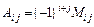где Мij – это определитель, полученный из определителя матрицы системы, путем вычеркивания строки с номером i, столбика с номером j.
,
,
,
,
,
,
,
,
.
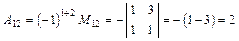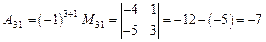Обратную матрицу вычислим по формуле
.
Получим обратную матрицу 
.
Далее воспользуемся формулой (6) для определения неизвестных x, y, z.
=
= 
, то есть, получено решение системы:
x = 2, y = 0, z = -1.
Правильность полученного результата устанавливаем с помощью проверки, подставляя найденные значения переменных х, y, z
в каждое уравнение системы
.
Ответ. (2, 0, 1).
Метод Гаусса
Одним из наиболее универсальных и эффективных методов решения систем линейных алгебраических уравнений является методГаусса, состоящий в последовательном исключении неизвестных.
Рассмотрим систему (1)
.
Процесс решения такой системы методом Гаусса состоит из трех этапов.
На первом этапе с помощью элементарных преобразований получают систему уравнений, эквивалентную системе (1). Другими словами систему (1) сводят к ступенчатому виду
(7)
где 
- коэффициенты при неизвестных и свободные члены, полученные в результате элементарных преобразований.
На втором этапе исследуют систему линейных алгебраических уравнений, то есть определяют количество ее решений по теореме
Кронекера - Капелли.
Теорема 1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы
.
Правила практического поиска всех решений совместной системы линейных уравнений вытекают из следующих теорем.
Теорема 2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение
.
Теорема 3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений
.
На третьем этапе последовательно находят все решения, начиная поиск неизвестных членов хi c последнего уравнения эквивалентной системы (7).
Пример 3. Решить систему методом Гаусса:
.
Решение. Переход к эквивалентной системе проведем с помощью элементарных преобразований расширенной матрицы заданной системы уравнений (получим нули под главной диагональю):
~ 
~ 
~ 
~ 
.
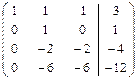