ѕ≥д час анал≥зу EEC та њхн≥х п≥дсистем у часткових пох≥дних застосовуютьс€ т≥льки р≥вн€нн€ г≥пербол≥чного й ел≥птичного типу. –≥вн€нн€ г≥пербол≥чного типу у форм≥ так званих телеграфних ≥ хви≠льових р≥вн€нь використовуютьс€ п≥д час анал≥зу електромагн≥тних процес≥в к≥л з розпод≥леними параметрами (л≥н≥й електропередач≥ електричних машин, трансформатор≥в тощо). ≈л≥птичн≥ р≥вн€нн€, на≠приклад у форм≥ р≥вн€нь Ћапласа та ѕуассона, застосовуютьс€ п≥д час розв'€зуванн€ задач теор≥њ електромагн≥тного пол€.
ƒе€к≥ методи розв'€зуванн€ г≥пербол≥чних р≥вн€нь. ” загальному випадку диференц≥йн≥ р≥вн€нн€ у часткових пох≥дних, под≥бно €к ≥ р≥вн€нн€ у звичайних пох≥дних, мають безл≥ч розв'€зань, ≥ дл€ вид≥ленн€ з них де€ких конкретних, однозначних розв'€зань необх≥дно задати певн≥ додатков≥ умови. ƒл€ г≥пербол≥чних р≥вн€нь ц≥ умови задають у форм≥ початкових ≥ крайових (граничних) умов.
¬ивченн€ метод≥в розв'€зуванн€ таких р≥вн€нь зд≥йснимо на при≠клад≥ р≥вн€нь однор≥дноњ багатопров≥дноњ л≥н≥њ, €к≥ запишемо у вигл€д≥ системи
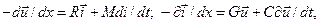
| (5.160) |
де 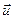 Ц багатовим≥рний вектор-стовпець напруг провод≥в (у тому числ≥ й трос≥в) в≥дносно земл≥;
Ц багатовим≥рний вектор-стовпець напруг провод≥в (у тому числ≥ й трос≥в) в≥дносно земл≥; 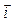 Ц в≥дпов≥дний вектор-стовпець струм≥в;
Ц в≥дпов≥дний вектор-стовпець струм≥в; 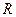 Ц квадратна матриц€ резистанс≥в петель пров≥д Ц земл€ (у
Ц квадратна матриц€ резистанс≥в петель пров≥д Ц земл€ (у 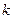 -му д≥агональному елемент≥ записуЇтьс€ сума резистансу
-му д≥агональному елемент≥ записуЇтьс€ сума резистансу 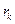
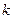 -го проводу й земл≥
-го проводу й земл≥ 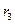 , у взаЇмних елементах Ц резистанси земл≥) на одиницю довжини л≥н≥њ;
, у взаЇмних елементах Ц резистанси земл≥) на одиницю довжини л≥н≥њ; 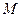 Ц квадратна матриц€ ≥ндуктивностей (записуютьс€ по д≥агонал≥) ≥ взаЇмо≥ндуктивностей (записуютьс€ у взаЇмних елементах) петель пров≥д Ц земл€ на одиницю довжини л≥н≥њ;
Ц квадратна матриц€ ≥ндуктивностей (записуютьс€ по д≥агонал≥) ≥ взаЇмо≥ндуктивностей (записуютьс€ у взаЇмних елементах) петель пров≥д Ц земл€ на одиницю довжини л≥н≥њ; 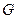 Ц квадратна матриц€ кондуктанс≥в на одиницю довжини л≥н≥њ
Ц квадратна матриц€ кондуктанс≥в на одиницю довжини л≥н≥њ 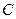 Ц квадратна мат≠риц€ динам≥чних Їмностей на одиницю довжини л≥н≥њ
Ц квадратна мат≠риц€ динам≥чних Їмностей на одиницю довжини л≥н≥њ 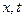 Ц аргументи (в≥д≠стань в≥д початку л≥н≥њ ≥ час). ѕоздовжн≥ параметри (коеф≥ц≥Їнти матриць
Ц аргументи (в≥д≠стань в≥д початку л≥н≥њ ≥ час). ѕоздовжн≥ параметри (коеф≥ц≥Їнти матриць 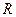 та
та 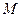 ) л≥н≥њ залежать в≥д частоти, поперечн≥ параметри (коеф≥≠ц≥Їнти матриць
) л≥н≥њ залежать в≥д частоти, поперечн≥ параметри (коеф≥≠ц≥Їнти матриць 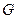 та
та 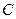 ) залежать в≥д напруг.
) залежать в≥д напруг.
ѕочатков≥ умови дл€ р≥вн€нн€ (5.160) задаютьс€ у вигл€д≥ законо≠м≥рностей розпод≥лу вектор≥в напруг ≥ струм≥в уздовж л≥н≥њ в початко≠вий момент часу, тобто
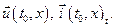
| (5.166) |
райов≥ (граничн≥) умови визначаютьс€ конкретними схемами к≥н≠цевих пристроњв ≥ записуютьс€ у вигл€д≥ р≥вн€нь стану цих пристроњв.
–≥вн€нн€ (5.160) можна записати також у координатах напруг 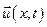 Ц зар€д≥в
Ц зар€д≥в 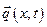 , €кщо п≥дставити
, €кщо п≥дставити
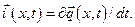
|
’вильовий метод. ¬≥н Ї узагальненн€м в≥домого з кур≠су теоретичних основ елек≠тротехн≥ки методу ƒ'јламбера. ¬икладемо цей метод у форм≥, розроблен≥й Ћен≥нградською школою електроенергетик≥вї —першу розгл€немо однофазну л≥н≥ю. «астосовуючи до њњ р≥вн€нь у вигл€д≥ (5.160) операторне перетворенн€, знаходимо (матриц≥ перетво≠рюютьс€ у власн≥ параметри, вектори Ц у скал€ри):
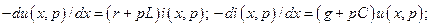
|
–озв'€зуванн€ г≥пербол≥чних р≥вн€нь на основ≥ њх зведенн€ до зви≠чайних диференц≥йних р≥вн€нь. “ак≥ методи широко застосовують завд€ки простот≥ й наочност≥. ƒл€ розв'€зуванн€ р≥вн€нь г≥пербол≥ч≠ного типу використовують звичайно метод пр€мих ≥ метод розд≥ленн€ зм≥нних.
|
|
|
ћетод пр€мих. ÷ей метод пол€гаЇ в апроксимац≥њ пох≥дних по одн≥й з незалежних зм≥нних в≥дношенн€м ск≥нченних прирост≥в функц≥й й аргументу, тобто по сут≥ в≥н Ї методом ск≥нченних р≥зниць по одному з аргумент≥в. “ака зам≥на пох≥дних по одному аргументу перетворюЇ диференц≥йн≥ р≥вн€нн€ у часткових пох≥дних по двох не≠залежних зм≥нних до вигл€ду звичайних диференц≥йних р≥вн€нь. ќчевидно, метод пр€мих справедливий дл€ будь-€ких тип≥в р≥вн€нь ” часткових пох≥дних (г≥пербол≥чних, ел≥птичних, парабол≥чних).
ѕ≥д час розв'€зуванн€ телеграфних р≥вн€нь (5.160) цей метод за≠стосовують по аргументу 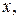 що набагато точн≥ше, н≥ж по аргументу
що набагато точн≥ше, н≥ж по аргументу 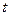 , бо в≥дносна зм≥на координат режиму вздовж л≥н≥й електропередач≥ набагато менша, н≥ж за часом. ќтже, при однаков≥й точност≥ по
, бо в≥дносна зм≥на координат режиму вздовж л≥н≥й електропередач≥ набагато менша, н≥ж за часом. ќтже, при однаков≥й точност≥ по 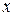 одержуЇмо значно менше ≥нтервал≥в, н≥ж по
одержуЇмо значно менше ≥нтервал≥в, н≥ж по 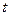 .
.
ћетод розд≥ленн€ зм≥нних (метод ‘урТЇ). —уть його пол€гаЇ у знаходженн≥ розв'€зань диференц≥йних р≥вн€нь у вигл€д≥ добутк≥в функц≥й окремих зм≥нних, п≥дставленн€ €ких у вих≥дне диференц≥йне р≥вн€нн€ в часткових пох≥дних даЇ змогу перетворити њх у систему звичайних диференц≥йних р≥вн€нь.
«астосуванн€ методу ‘ур'Ї справедливе т≥льки дл€ одновим≥рного р≥вн€нн€. “ому в задачах електроенергетики дл€ ≥нтегруванн€ телеграфних р≥вн€нь в≥н вико≠ристовуЇтьс€ у поЇднанн≥ з методами, €к≥ дають змогу зводити багатофазн≥ системи до однофазних.
ќтже, класичним прикладом г≥пербол≥чних р≥вн€нь дл€ застосуванн€ цього ме≠тоду е система вигл€ду.
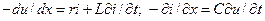
| (5.183) |






