В качестве примера рассмотрим класс двухкомпонентных АИА (2-АИА), определенных следующим образом:
I. Каждый АИА воспринимает только одну компоненту информации и творит тоже только по одной информационной компоненте.
II. Для каждого АИА одна компонента описывает процесс, а другая - состояние.
III. Для каждого АИА одна компонента рациональны, а другая - иррациональна.
Как следует из вышесказанного, этот класс АИА является простейшим из возможных. Будем обозначать такие АИА как 2-АИА.
Корректное определение 2-АИА как объекта, реализующего те или иные режимы управления на данном уровне иерархии в ИСС, возможно лишь только так, как описано выше:
· Действительно: первым условием определяется то, что АИА имеет лишь только две компоненты.
· Если принять, что 2-АИА и программируются процессом и творят также процесс, то мы не получим оптимального управления. Например, рассмотрим 2-АИА <П-Топ|П-КС>, который программируется процессами на всем иерархическом уровне и творит процессы же, изменяя отдельные КС. В этом случае "результатом труда" такого 2-АИА было бы беспрерывное и безостановочное изменение в отдельной (отдельных) КС, так как имеет место кольцо положительной обратной связи: 2-АИА "видит" процесс - но никогда сам не сумеет его остановить (то есть "зафиксировать состояние")! Аналогично если бы 2-АИА строился только лишь "на состояниях", то он никогда не сумел бы "запустить" ни одного процесса. Конечно, оптимального управления с использованием таких АИА достигнуто быть не может! Таким образом, второе условие является прямым следствием требования оптимальности управления.
· А если определить 2-АИА так, чтобы одни из них реализовывали управление только по рациональным компонентам, а другие только по иррациональным, - то придется вводить специальный тип АИА, который бы "анализировал ситуацию на всем иерархическом уровне и раздавал бы задания таким "однорациональным" АИА". Зачем это делать? Поэтому третье условие также следует из требования оптимальности управления, реализуемого системой 2-АИА.
Таким образом, 2-АИА преобразует одну компоненту информации (посредством своей "программной функции") в другую (своей "творческой функцией").
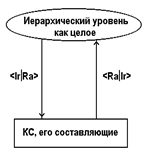
Другими словами, 2-АИА устроены таким образом, что одна из их компонент (будем для нее также использовать название "функция") соответствует рассматриваемому уровню иерархии в ИСС как целом, а вторая ее компонента соответствует конкретным КС, из которых этот уровень состоит. Схематически это показано на Рис.1, где через Ir и Ra обозначены иррациональная и рациональная компоненты информации, соответственно. Из Рис. 1 видно, что класс 2-АИА вследствие условия III формирует кольца обратной связи.
|
Условиями I-III класс 2-АИА определен однозначно и состоит из 16 различных типов, перечисленных в Таблице I во Введении.
16 типов 2-АИА структурируются Теоремой 1.
Теорема 1. Система (класс) 2-АИА самоорганизуется в 4 кольца самопрограммирования (кольца адекватной передачи информации, кольца выработки нового режима управления).
Доказательство. Произвольный 2-АИА может адекватно воспринять информацию только от того 2-АИА, у которого вторая (творческая) функция эквивалентна его первой (программной) функции. Таким образом, условие адекватной передачи информации от одного 2-АИА к другому задает отношение упорядочения на множестве 2-АИА. Поэтому класс 2-АИА распадается на 4 непересекающиеся группы: внутри каждой из которых информация движется от одного 2-АИА до другого. Конец доказательства.
Введенные таким образом 4 кольца самопрограммирования могут быть записаны так:
| <С-Топ½П-КС> Þ <П-КС½С-Мемб> Þ <С-Мемб½П-Отн> Þ <П-Отн½С-Топ> Þ <С-Топ½П-КС> Þ... | (2a) |
| <П-Мемб½С-Отн> Þ <С-Отн½П-Топ> Þ <П-Топ½С-КС> Þ <С-КС½П-Мемб> Þ <П-Мемб½С-Отн> Þ... | (2b) |
| <С-Отн½П-Мемб> Þ <П-Мемб½С-КС> Þ <С-КС½П-Топ> Þ <П-Топ½С-Отн> Þ <С-Отн½П-Мемб>Þ... | (2c) |
| <П-КС½С-Топ> Þ <С-Топ½П-Отн> Þ <П-Отн½С-Мемб> Þ <С-Мемб½П-КС> Þ <П-КС½С-Топ>Þ... | (2d) |
Замечание 5. Ситуация, когда два 2-АИА, которые имеют вид <F1|F2> и <F2|F1> соответственно (Fi - информационные компоненты), реализуют совместное управление тем же самым объектом (объектами), является конфликтной: так как при этом один 2-АИА разрушает ту же самую информационную компоненту, которую только что сотворил другой 2-АИА.
Замечание 6. 2-АИА может воспринимать не только информацию от предыдущего 2-АИА в соответствующем кольце самопрограммирования, но, в общем случае, также и другую (получаемую от других 2-АИА) информацию в рамках своей программной функции. А также - интерпретировать деятельность других 2-АИА в рамках своей творческой функции.
Теорема 2. Система 2-АИА самоорганизуется в 2 спаренных кольца самопрограммирования (кольца адекватной передачи информации, кольца выработки оптимального управления), которые определяются однозначно и в которых и воспринимаются, и творятся все 8 компонент информации.
Доказательство. Рассмотрим (2). Два кольца адекватной передачи информации могут быть объединены в единое кольцо, в котором все "звенья" функционируют совместно, только в том случае, когда два 2-АИА, которые находятся в одном и том же звене, реализуют совместно бесконфликтное управление.
Рассмотрим произвольный 2-АИА, - например,
<С-Топ½П-КС> (3)
Этот 2-АИА "работает" с двумя компонентами информации. На компоненту С-Топ он опирается как на заданность (то есть - программируется ею), а творит он по компоненте информации П-КС (то есть - он изменяет процессы в единичных объектах для рассматриваемого уровня иерархии). Однако активность нашего 2-АИА будет возможна лишь только в случае, когда состояние взаимодействия между КС (единичными объектами для данного уровня)) являются фиксированными: в противном случае отсутствует "инструмент" как для фиксирования, так и для изменения состояния для рассматриваемого иерархического уровня. Такое состояние взаимодействия между КС как фиксирует тот 2-АИА, который имеет С-Отн как вторую (творческую) функцию. Как видно из (2), требуемый 2-АИА находится только в кольце (2b). И более того: для объединенных таким способом двух колец - (2a) и (2b) - рассмотренная выше "дополнительность" имеет место для всех звеньев в этом спаренном кольце самопрограммирования.
Если рассмотреть программные функции 2-АИА, то придем к тем же самым результатам. Действительно, состояние внутреннего строения для иерархического уровня как целого может быть совместимо только с процессами на мембране: так как если топологическое строение уровня фиксировано, то только процессы на мембране могут иметь место как отклик на внешнее воздействие.
Кольца (2c) и (2d) могут быть объединены аналогично. Конец доказательства.
Таким образом, система 2-АИА разбивается на 2 спаренных кольца 2-АИА, которые связаны между собой отношениями самопрограммирования (будем использовать термин "дуальная пара" для двух 2-АИА из одного и того же звена из Теоремы 2).
Из Теоремы 2 вытекает следующее следствие.
Следствие. Два 2-АИА будут оптимально (бесконфликтно) управлять (то есть - реализовывать адекватное преобразование информации) при выполнении таких условий:
a) программные функции этих 2-АИА есть одновременно либо рациональные, либо иррациональные;
b) программная функция одного 2-АИА описывает процесс, а другого - описывает состояние;
c) программные функции для обоих 2-АИА описываются различными компонентами информации.
Для творческих функций вследствие условия II из определения 2-АИА будут справедливы те же самые условия.
Интересно, что дуальная пара 2-АИА реализует управление только или по Ir -, или по Ra - информационным компонентам (см. Рис. 1). Такое управление является оптимальным, что следует из Теоремы 2.
Новая информация может поступать в популяцию[14] 2-АИА через произвольный 2-АИА (то есть от произвольного 2-АИА). Максимально полная реализация управления (то есть - изменение всей информации на рассматриваемом уровне ИСС) имеет место только в случае, когда каждый вид 2-АИА будет принимать участие в преобразовании информации (в выработке совместного режима управления). Можно сказать, что только при этих условиях может быть получена "социализация" новой информации, и вследствие этого будут разработаны "нормативные" (общепринятые) новые алгоритмы управления (информации, которая необходима для управления), при помощи которых действуют 2-АИА.
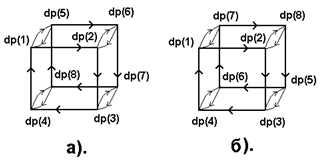
Легко видеть, что такая организация обработки новой информации и социализации ее на иерархический уровень ИСС (то есть - управление этим уровнем ИСС) может быть осуществлено путем самоорганизации всех 16 2-АИА в 2 структуры (кольца) самопрограммирования[15], которые в общем случае должны работать совместно. В одной такой структуре преобразуются Ir - информационныекомпоненты, а в другой такой структуре трансформируются Ra - информационные компоненты (см. Рис. 2: a) есть Ir -, и b) есть Ra - кольца самопрограммирования, соответственно; в вершинах представлены дуальные пары, - обозначение см. в Таблице I во Введении).
В Ir - кольце самопрограммирования происходит социализация иррациональной компоненты информации (например, обогащение языка новыми структурами). В творческом плане в Ir - структуре самопрограммирования происходит формирование информации об иерархическом уровне как целом, так как для каждого "звена" в такой структуре рациональные компоненты фиксированы.
|
В Ra - структуре самопрограммирования происходит социализация рациональных компонент информации, соответственно.
Отметим, что только при таком способе построения колец самопрограммирования все 4 2-АИА, которые находятся в той же самой "вершине", имеют одновременно или рациональные, или же иррациональные программные функции. При любых других способах конструирования таких структур будут иметь место случаи, когда в одной и той же вершине как рациональные, так и иррациональные компоненты информации будут использоваться разными 2-АИА в качестве программных. Однако такое управление будет конфликтным, так как в этих условиях два 2-АИА, находящиеся в той же вершине, одновременно должны работать в противоположных направлениях: один, базируясь на фиксированных свойствах иерархического уровня как целого, создает КС (состояния или процессы) или отношения между КС, тогда как второй - совершенно наоборот. Другими словами, работая в той же вершине, один 2-АИА создает состояния (процессы), тогда как другой эти же состояния (процессы) немедленно разрушает. Очевидно, что управление, реализуемое таким структурами, является конфликтным.
Таким образом, имеет место следующая теорема.
теорема 3.Вследствие необходимости социализации новой информации, которая нужна для управления иерархическим уровнем ИСС, во всю совокупность 2-АИА, все 16 2-АИА самоорганизуются в два описанных выше кольца самопрограммирования, в которых происходит социализация Ir - и Ra - информационных компонент.
Так как два описанных выше кольца самопрограммирования работают одновременно, и так как передача информации в этих структурах однонаправленна, систему из всех 16 различных 2-АИА в этих двух структур можно рассматривать как объект с нетривиальным топологическим строением.
Рассматривая Рис. 2 как развертку двумерного многообразия, а направление передачи информации (самопрограммирования) как способ задания ориентации многообразия, с использованием стандартных топологических методов[16] получаем следующую теорему:
Теорема 4. Направление самопрограммирования при социализации новой информации, которая необходима для управления иерархическим уровнем ИСС, приводит к самоорганизации всех 16 различных 2-АИА в единую структуру (объект) нового иерархического уровня управления, - в структуру, топологическое строение которой диффеоморфно двумерной сфере с 7 вклеенными пленками Мебиуса.
Отметим, что из Теоремы 4 может быть разработан новый математический формализм для описания процессов переработки информации.
Определение 9. Объект, который описывается Теоремой 4, мы будем называть соционом (подчеркивая тот факт, что управление данным иерархическим уровнем ИСС может быть осуществлено только совместной, кооперативной, социальной активностью всех 16 2-АИА).
Следствие 1. Эйлерово число для социона есть c=-5.
Следствие 2. Топологическое строение социона гомотопически эквивалентно букету из 6 окружностей.
Базируясь на описанном в этом разделе множестве 2-АИА может быть построена ИСС для осуществления управления в Природных и Социальных ИСС: в этой "управляющей" ИСС каждый единичный управляющий объект эквивалентен (в смысле управления) определенной 2-АИА, а объекты нового иерархического уровня управления возникают путем самоорганизации 16 таких новых 2-АИА в социон.
Теорема 5. Если соционы удовлетворяют условиям I-III, то каждый такой социон может быть описан как определенный 2-АИА, с помощью которого реализуется управление на соответствующем иерархическом уровне. Такая управляющая ИСС, которая может быть сконструирована из соответствующих 2-АИА (реализующих управление на соответствующих иерархических уровнях), есть самоорганизованная ИСС для реализации управления в том смысле, что на каждом ее уровне используются как те же самые единичные конструкции для управления, так и те же самые методы управления.
Следствие 1. Для произвольно сложной Природной или Социальной ИСС может быть сформирована путем самоорганизации иерархическая система из 2-АИА, которые реализуют управление такими ИСС. "Начальные" 2-АИА (для наиболее низкого уровня управления ИСС) могут осуществлять преобразование информации на произвольно низком уровне иерархии в Природной или Социальной ИСС (например, эти 2-АИА могут основываться на достаточно полной системе аксиом, описывающей произвольно низкий иерархический уровень в Природной или Социальной ИСС).
Четырехкомпонентные АИА
Так как кольца самопрограммирования, которые необходимы для конструирования социона, состоят из дуальных пар 2-АИА, то получаем теорему:
Теорема 6. Для восьми 4-АИА (сохраняя обозначения, которые были использованы для дуальных пар - см. Введение и Таблицу I во Введении)
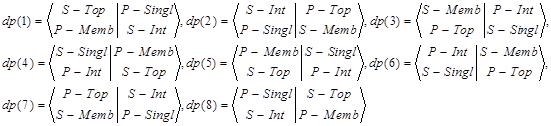
которые сконструированы с использованием Следствия 1 из Теоремы 2 справедливы, как Теоремы 3-5, так и Следствия из них. Компоненты информации внутри как программных, так и творческих функций перестановочны.
Другими словами, с точки зрения информационной динамики и управления классы как 2-АИА, так и 4-АИА являются эквивалентными в смысле возможностей для конструирования ИСС, которые могут осуществлять управление в Природных и Социальных ИСС.
Следствие 1. Если социон, сконструированный из 2-АИА или 4-АИА, удовлетворяет условиям Теоремы 5 или Теоремы 6, то из этих соционов (которые сами являются 2-АИА или 4-АИА для каждого иерархического уровня и имеют одинаковое топологическое строение) может быть сконструирована иерархическая управленческая система для управления Природными или Социальными ИСС, которая описана в Теореме 5,.
В общем случае могут быть сконструированы для конкретных нужд (реализации управления в некоторых специфических ИСС) также и АИА, которые отличаются от 2-АИА и 4-АИА. Например, - с m входами и n выходами (в общем случае m¹n). Кроме того могут быть случаи, когда некоторые АИА могут программироваться и/или творить на разных иерархических уровнях тех же самых (или - разных) Природных или Социальных систем. В ряде случаев это может приводить к объектам с топологическим строением, которое отличается от социона.
1.3. Режимы управления как типы личности
...иногда при анализе старых понятий создается новая наука.
В.И. Вернадский, "Научная мысль как планетное явление"
Дадим характеристику 2-АИА для социальных ИСС, когда данный иерархический уровень как целое - это совокупность всех людей, Человек в обобщенном смысле. Конкретный же объект - КС - это конкретный отдельный человек. Поэтому трактовку компонент информации при описании как людей, так и их отношений друг с другом удобно выражать в антропоморфном виде.
Для рациональных компонент информации КС - это конкретный человек. Тогда С-КС и П-КС компоненты информации описывают соответственно состояния и процессы как происходящие с конкретным человеком, так и те, в которых он непосредственно участвует. Их можно называть логикой, так как ими описывается порядок следования событий, причинность, общие для некоторого класса объектов (КС) характеристики и т.п. на уровне конкретных объектов: весь комплекс информации, описывающей поведение индивидуального человека обычно связывают именно с логикой. (В частности, именно логика определяет способ объединения совокупности из нескольких объектов в некую общность.) В типологии Юнга-Майерс-Бриггс[17] (MBTI® types of personality) эти компоненты информации названы "рассудочностью" (thinking).
С-Отн и П-Отн соответствуют компонентам информации, с помощью которых можно описать состояния и процессы во взаимодействии людей друг с другом. Их можно назвать этикой, подчеркивая то обстоятельство, что весь комплекс информации об отношениях между людьми (в общем случае - об отношениях между КС) обычно полагают предметом именно этики. Следует отметить, что состояние отношений естественно связать с эмоциями - как способом сокращенного их описания. В типологии Юнга-Майерс-Бриггс эти компоненты информации названы "эмоциями" (feeling).
Для интерпретации иррациональных компонент надо учесть следующее. Восприятие объекта - конкретного человека - по компоненте С-Топ означает осознание его места (его “важности”, его "принадлежности", его "причастности") в структуре данного социального уровня как целого. Компонента П-Топ описывает процесс перестройки структуры рассматриваемого социального уровня как целого, и восприятие конкретного человека по этой компоненте означает осознание причастности данного человека к такому процессу, - что задает также некоторые временные интервалы. В типологии Юнга-Майерс-Бриггс эти компоненты информации названы "интуицией" (intuition).
Компонента информации С-Мемб описывает состояние границы между данным социальным уровнем как целым и его окружением, что позволяет проводить разграничение на “внутреннее” и “внешнее”, а также - осознавать место данного человека и его возможности относительно принадлежности его к мембране и к "своим", - в частности его способность противостоять всему “внешнему”, успешно “защищать” данный социальный уровень как целое (а также свои собственные интересы, конечно!). Компонента П-Мемб описывает процесс реструктурирования мембраны, - на уровне конкретного человека этому соответствуют сенсорные ощущения во всем их спектре (весь комплекс сенсорных ощущений связан именно с поверхностью соответствующих органов человека). В типологии Юнга-Майерс-Бриггс эти компоненты информации названы "сенсорикой" (sensation).
Все 2-АИА, программируемые состоянием, порождают процесс. Такие типы называют “ экстравертами ” - "направленными наружу" в своей деятельности (типологии Юнга-Майерс-Бриггс используется термин extraversion). Все 2-АИА, программируемые процессом, порождают состояние - они называются “ интровертами ” - соответственно "направленными внутрь" себя (introversion).
Все 2-АИА, которые программируются иррациональными компонентами информации, называются иррациональными, - и наоборот, те, которые программируются рациональными компонентами - рациональными. Образно можно сказать, что иррациональные типы программируются преимущественно “идеями” (ибо только в такой неоднозначной форме можно выразить вербально те характеристики информации, которые относятся к рассматриваемому иерархическому уровню как целому; - это особенно наглядно для социальных иерархических уровней, для которых такое описание действительно возможно только на уровне идей “общечеловеческого характера”!), а рациональные - преимущественно “словами” (ибо на уровне конкретных КС и их взаимодействий допускается большая конкретность в вербальном выражении их характеристик).
Подытожим:
тип 2-АИА на социальном уровне определяется последовательным применением четырех дихотомий: "рациональный - иррациональный", "экстраверт - интроверт", "логик - этик" и "сенсорик - интуит". Такое деление можно производить в произвольном порядке - см. Приложение 1.
В типологии Юнга-Майерс-Бриггс (MBTI types of personality) терминов иррациональность и рациональность нет: вместо них вводятся термины judging (решающий) и perceiving (воспринимающий). Если в представлении типа как 2-АИА (в нашей терминологии) имеется описывающая состояние рациональная компонента информации - то используется обозначение judging, а если рациональная компонента информации описывает процесс - то используется обозначение perceiving.
Нетрудно видеть, что типология 2-АИА является тождественной типологии Юнга-Майерс-Бриггс - см. Таблицу 1 во Введении, в которой приведены также широко используемые[18] в США ролевые псевдонимы для названий типов.
Типология Юнга-Майерс-Бриггс более полувека широко используется в экономически развитых странах, но только в наших книгах она получила свое теоретическое обоснование. Весьма принципиальной особенностью оказалось то, что эта - считавшаяся ранее психологической! - типология не имеет ничего общего с психологией: все маркеры типов (большая часть которых получена впервые нами с использованием результатов, изложенных в предыдущей и этой наших книгах) проявляются исключительно через деятельность человека и могут быть объективно зафиксированы, - в отличие от используемых в психологии нечетких и часто крайне двусмысленных понятий. Вследствие этого, рассматривая тип человека как присущий ему режим управления Реальностью, можно не только ставить вопрос о соответствии типа человека и функциональных обязанностей той или иной специальности, - но и решать вопрос о профессиональной пригодности данного человека.
В качестве методического примера[19] опишем, как теоретически найти типы личности, оптимальные для профессиональной деятельности пилота самолета (пилота космического летательного аппарата, водителя автомобиля или иного движущегося объекта). Пилот должен реагировать на состояние окружающей среды - то есть программная функция его должна описывать состояние (иными словами - он должен быть экстравертом).
Причем желательно, чтобы эта компонента информации описывала либо состояния конкретного объекта (самолета, КЛА) - и была, следовательно, логикой, либо состояния границы всего рассматриваемого иерархического уровня как целого - и была соответственно сенсорикой (ибо события на границе уровня предшествуют появлению топологических событий).
Итак, сразу выделяются как подходящие для управления самолетом типы личности < С-КС |П-Топ > и < С-КС |П-Мемб >, то есть ЛСЭ и ЛИЭ (обозначения см. в Таблице 1 во Введении). Причем у ЛСЭ должны быть преимущества перед ЛИЭ, так как панель управления расположена на поверхности (границе), что как раз подходит творческой функции ЛСЭ.
Далее: пилот должен в ответ на внешние события манипулировать конкретным объектом (самолетом, КЛА), но совсем не отношениями между объектами, то есть творческая функция его должна быть П-КС. Тогда из возможного выбора творческих компонент информации для иррациональной программной функции С-Мемб получаем < С-Мемб|П-КС >, то есть - СЛЭ.
При этом именно СЛЭ в нестандартных ситуациях должен проявлять оптимальное и адекватное понимание, реагирование, описание событий и коммуникацию, так как его творческая функция управляет динамикой конкретного объекта (отсюда и его адекватные ситуации и комментарии, и действия), тогда как и у ЛСЭ, или у ЛИЭ творческие функции относятся ко всему иерархическому уровню в целом - отсюда и менее конкретная вербализация как ситуации, так и собственных действий (а также и относительная шаблонность действия, вследствие чего более быстрая, чем у СЛЭ, обучаемость).
Полученные результаты имеют полное подтверждение: экспериментально исследовано[20] влияние типа личности на качество подготовки летчиков (объем выборки 30 человек).
Выявлено, что именно представители типов ЛСЭ и СЛЭ добиваются наилучших результатов в процессе предполетного обучения на тренажерах и требуют наименьшего количества вывозных (перед самостоятельным) полетов при высоком их качестве, - в результате чего сделан вывод о том, что представители именно этих двух типов - СЛЭ и ЛСЭ - являются наиболее подходящими для овладения профессией летчика. Также в экспериментах отмечено, что в экстремальных условиях именно у СЛЭ наблюдаются лучшие как ориентировка в ситуации, так и речевой обмен с инструктором.
Поскольку разработанный формализм достаточно общ, а тип есть режим управления, реализуемый данным человеком (причем, как отмечено еще Юнгом, тип человека остается неизменным на протяжении его жизни), то получены новые маркеры типов, большинство из которых связано непосредственно с профессиональной деятельностью человека. Поэтому выраженные в терминах настоящей работы особенности функционирования типа успешно используются при определении эффективности выполнения человеком заданных профессиональных обязанностей.
1.4. Самоорганизация людей для выработки новых режимов управления (отношения между типами личности)
Мы называем систему самоорганизующейся, если она без специфического воздействия извне обретает какую - то пространственную, временную или функциональную структуру.
Г. Хакен, "Информация и самоорганизация"
Для обеспечения оптимального функционирования в составе социона каждый из 2-АИА должен обладать способностью к осуществлению постоянного обмена информацией с несколькими другими 2-АИА (то есть обладать способностью находиться в постоянном контакте одновременно со всеми ними). Оптимально - с 7 другими 2-АИА: со своими дуалом, с двумя дуальными парами (с которыми он находится в одном звене в Ir - и Ra -кольцах - см. Рис.2 в параграфе 1.2), и еще с двумя 2-АИА (один их которых программирует его, а другого - программирует он). Для того, чтобы данный 2-АИА вообще мог участвовать в работе социона, он должен обладать способностью одновременно удерживать в своем внимании не менее 5 других 2-АИА (своего дуала + 2 дуальные пары - по одной из Ir - и Ra -колец). Максимальное же число коммуникантов, которое может без ущерба для оптимальной работы социона удерживать во внимании данный 2-АИА, есть 9 (к 7 упомянутым ранее необходимо добавить еще 2-х: того, который программирует его дуала и того, которого его дуал - программирует). Итак, доказана справедливость теоремы:
Теорема 7. Для того, чтобы иметь возможность участвовать в работе социона (то есть для того, чтобы 2-АИА мог участвовать в выработке нового режима управления), каждый 2-АИА должен обладать способностью удерживать в своем внимании одновременно 7±2 своих коммуникантов.
Тем самым получено, вероятно, первое доказательство того известного из психологии восприятия, коммуникации и менеджмента факта[21], что устойчивая коммуникация возможна лишь с 7±2 коммуникантами (большее их количество приводит к структурированию коммуникантов в отдельные группы).
Поскольку отношения самопрограммирования 2-АИА однонаправленны, нетрудно видеть (например, из Рис. 2 параграфе 1.2), что в соционе они задают 5 пар разных типов отношений упорядочения, которые собраны в Таблице 2 во Введении. Гетеровертные отношения - отношений между интровертом и экстравертом, гомовертные - в противном случае. А, Б и В - это отношения между обоими рациональными или обоими иррациональными типами, а Г и Д - между рациональным и иррациональным типами.
Всего же разных типов отношений между 2-АИА есть 16 - к 10 из Таблицы 2 надо добавить отношения тождества (между двумя одинаковыми типами), дуальные, 2 отношения самопрограммирования (“передача” и “прием” информации), и еще 2 - по одному с дуалами "приемника" и "передатчика" (или, что то же самое, с передатчиком и приемником своего дуала). Последние 4 отношения - асимметричные. Таким образом, наличие таких 16 интертипных отношений является следствием топологического строения социона (которое, в свою очередь, задается определением 2-АИА - алгебраическое доказательство см. ниже в конце этого параграфа). Итак, получаем теорему
Теорема 8. При выработке нового режима управления (в процессе социализации - освоения новой информации) между 2-АИА возможны только 16 типов отношений.
Эксперименты убедительно свидетельствуют, что эффективность выполнения задач в условиях изменчивости обстановки прямо зависит от вида интертипных отношений: например, экспериментально обнаружено[22], что уровень успешности в выполнении задач летными экипажами (обследовано 19 летных экипажей армейской авиации) напрямую зависит от степени оптимальности для реализации управления интертипных отношений.
Собственные наблюдения (наблюдалось несколько сотен отношений между конкретными людьми) показывают, что характеристика отношений между типами людей, которая основана на развитом выше формализме, адекватно описывают реальность. Отметим, что отношения между конкретными людьми описывались исходя исключительно только из их уже известных типов: вначале определялись типы людей, а после - им сообщалась теоретическая характеристика отношений для конкретной пары людей. Таким образом, при каждом описании пары типов производилась апробация развитого в работе формализма. Подробное описание отношений представлено в нашей книге "Социальные Технологии...".
Итак,
описанный формализм позволяет впервые математически однозначно описать отношения между типами людей, которые возникают при освоении новой информации.
Легко видеть, что при самопрограммировании (в индивидуальном и дуальном кольцах, - а также в составе социона) каждый из 2-АИА в ответ на поступившую новую информацию вырабатывает свой собственный режим управления, причем совсем не тот, которого "хотел" от него другой 2-АИА (например, - его передатчик). Тем самым среди людей реализуется определенный вариант метода "проб и ошибок", известный как "ассоциативный режим управления". И хотя для нормативных ситуаций (когда знания, умения, навыки и опыт у всех коммуникантов одинаковы[23]) этот метод поиска решения весьма неоптимален, такая деятельность может принести успех - но лишь только в тех ситуациях, которые вызваны НОВЫМИ, ранее не наблюдавшимися воздействиями (и требуют поэтому выработки НОВЫХ режимов управления). Интересно, что реализация такого метода обычно вызывает огромные затруднения при математическом моделировании функционирования и деятельности живых организмов, а особенно - мышления Человека. Невозможность адекватного разрешения такой ситуации, имеющая место при классическом подходе к моделированию Человека, ранее не позволяли приступить к моделированию развития Человечества: возникновение НОВОГО может быть описано лишь только в терминах такого АССОЦИАТИВНОГО, ЭВРИСТИЧЕСКОГО мышления. Интересно, что одновременно получен также и механизм формирования нового нормативного блока, который закрепляется - социализируется, вербализируется - в случае успеха. Таким образом, на социальном уровне кольца индивидуального и дуального самопрограммирования реализуют способ ассоциативного управления природными и социальными системами!
Способность Человека по-разному воспринимать высказывания других людей - то есть ассоциативность восприятия - часто оказывается источником нового знания. Такое "непонимание" одного человека другим часто выступает как "побудительный мотив" к получению новых знаний.
Несколько примеров из истории физики: эта область знакома нам очень хорошо - и, к тому же, ее история "задокументирована" наиболее полно.
1) Ричард Фейнман искренне полагал, что он всего лишь "детализировал" одно из высказываний Поля Дирака, которое тот привел в "слишком кратком" виде в одной из его статей. Оказалось же, что Р. Фейнманом разработан новый формализм, и притом настолько мощный, что позволил за пару часов (в буквальном смысле слова!) выполнить расчет, на который квалифицированный физик потратил несколько месяцев работы: Р. Фейнман прослушал доклад одного из физиков о выполненной работе и на следующий день принес решение более общей ситуации! И лишь после этого формализм так называемых "Фейнмановских диаграмм" был опубликован, - за что его автор и получил впоследствии Нобелевскую премию.
2) Эрвин Шредингер, записывая впервые свое уравнение, был уверен, что он просто приводит "более удобную" форму предоставления материала диссертации Луи де-Бройля (снова Нобелевская премия).
3) Давид Гильберт, впервые услышав о "матричной квантовой механике" Вернера Гейзенберга, сказал, что матрицы "сами по себе" в математике не встречаются: они всегда появляются на промежуточных этапах решения так называемых "краевых задач" теории дифференциальных уравнений в частных производных. Физики над ним втихомолку посмеялись ("Гильберт ничего не понял!"), - но потом, после появления уравнения Шредингера, над ними смеялся уже Д. Гильберт.
АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ ОТНОШЕНИЙ МЕЖДУ ТИПАМИ
Операторы на множестве 2-АИА как исчисление на множестве режимов управления. Нетрудно видеть, что каждый из типов 2-АИА может быть описан в виде 4-компонентного вектора вида {a,b,c,d}, где первые два компонента описывают программную функцию 2-АИА (первый - ее рациональность или иррациональность, а второй - конкретный класс информации, к которому она относится), а последние два компонента описывают творческую функцию 2-АИА (третий компонент вектора описывает конкретный класс информации, к которому принадлежит творческая функция, а четвертый - описывает творческая компонента информации состояние или процесс). Заметим, что вследствие такого определения вторая и третья компоненты вектора типа 2-АИА имеют разную рациональность (в частности, при смене рациональности типа 2-АИА вторая и третья компоненты вектора типа должны поменяться местами). Такая форма записи однозначно соответствует сокращенным аббревиатурам записи типа из Таблицы 1 во Введении.
Как следует из приведенного выше определения для записи типа 2-АИА, каждая компонента вектора типа может принимать два значения - 0 или 1 (выбор фиксации конкретных соответствий значений переменных для дальнейшего несущественен). Таким образом, тип как вектор может быть записан как {a,b,c,d}, где a,b,c,d=0,1. Обозначим множество векторов типов 2-АИА через {Тi}.
Введем класс операторов, которые определены на множестве векторов типов 2-АИА и которые переводят один тип в другой. Легко видеть, что этот класс операторов может быть представлен как покомпонентное сложение вектора типа с 4-компонентным вектором, которые является представлением соответствующего оператора. Сложение должно производиться по mod 2 (таким образом, компоненты всех векторов образуют в алгебраическом смысле поле из двух элементов 0 и 1 - см.[24]).
Базис этого представления операторов образуют 4 вектора, которые можно записать как e1={1,0,0,0}, e2={0,1,0,0}, e3={0,0,1,0} и e4={0,0,0,1}.
Легко видеть, что существует только 16 различных операторов, переводящих один тип в другой: исключая 4 базисные векторы и нулевой вектор e0={0,0,0,0} (тождественное преобразование) это векторы e5= e1+ e2, e6=e1+ e3, e7=e1+ e4, e8=e2+ e3, e9=e2+ e4, e10=e3+ e4, e11=e1+ e2+ e3, e12=e1+ e2+ e4, e13=e1+ e3+ e4, e14=e2+ e3+ e4, e15=e1+ e2+ e3+ e4. Так как после действия оператора e1 изменяется рациональность типа - и одновременно меняются местами рациональные и иррациональные классы информации, то для операторов e5 - e15 операцию перевода "типа в тип" - то есть "закон суммирования" для компонент информации - определим так: оператор e1 действует первым (изменяя рациональность типа), вследствие чего вторые и третьи компоненты вектора типа меняются местами, а уже после этого имеет место действие других базисных операторов (то есть происходит суммирование с другими компонентами вектора типа еi при i>1). Вследствие этого условия совокупность операторов e0 - e15 будет рассматриваться как совокупность упорядоченных операторов в смысле В.П. Маслова - см.[25].
Структуру множества операторов {ei} задает следующий блок теорем:
Теорема 9. Совокупность операторов {ei} образует группу некоммутативную, так как, например, e7•e13¹e13•e7).
Теорема 10. Группа {ei} имеет 11 циклических подгрупп порядка 2.
Теорема 11. Группа {ei} распадается на 3 вида комплексов, элементы которых обладают следующими свойствами: e0•e0=e0 (1 комплекс), ei•ei=ei2=e0 (11 наборов комплексов - циклических подгрупп порядка 2, - такие операторы будем называть "симметричными"), и ei4=e0 (4 набора комплексов - циклических подгрупп порядка 4, - такие операторы будем называть "асимметричными").
Теорема 12. Группа {ei} является векторным пространством, размерность которого равна 4.
Следствие 1. Если описаны действия любых 4 линейно независимых операторов из {ei}, то действие остальных 11 операторов может быть выражено в терминах действия этих операторов (действие тождественного оператора e0 - тривиально).
Асимметричные операторы из {ei} структурируют множество типов 2-АИА {Тi}:
Теорема 13. Множество типов 2-АИА {Тi} каждым из асимметричных операторов разбивается на 4 равномощных непересекающихся подмножества (4 орбиты, содержащие соответственно по 4 разных типа 2-АИА).
Следствие 1. Множество {Тi} есть сумма 4 множеств, каждое из которых образовано оператором, обладающим свойством ei4=e0.
Определение 10. Оператор ei из {ei}, переводящий один тип 2-АИА в другой, будем называть отношением между данными типами 2-АИА.
Таким образом, на множестве типов 2-АИА имеется 16 отношений: 1 - тождественное отношение, 11 - симметричныхотношений (когда последовательное применение операторов перехода от типа к типу не выводит за пределы этой пары типов), и 4 асимметричныхотношений (когда последовательным применением данного отношения 4 разных типа 2-АИА замыкаются в кольцо).
Асимметричное отношение e13 является выделенным, так как именно оно обеспечивает наиболее высокую степень самопрограммирования между парой 2-АИА. Действительно: только при таком соотношении между этими 2-АИА творческая функция первого 2-АИА совпадает с программной функцией второго 2-АИА. Иными словами, активность первого 2-АИА вторым 2-АИА воспринимается как вполне равнозначная замена всему окружающему миру (ведь этот второй 2-АИА "видит" лишь только одну компоненту информации - причем как раз ту, которая является творческой для первого 2-АИА).
Совокупность операторов {ei} можно представить также в виде графов - отрезков, соединяющих две точки (два 2-АИА разных типов). Тогда легко видеть, что асимметричные отношения представимы в виде ориентированных графов.
Наконец, как следует из определения операторов {ei}, если любой асимметричный оператор применить дважды,. то получим симметричный оператор: ei2=e8. Имеются следующие соотношения: e12 • e13 = e13 • e12 = e5 • e6 = e6 • e5 = e0. Наличие "перекрестных" соотношений e14 • e5 = e13 и e14 • e6 = e12 и подобных им позволяет выделить отношение e14 среди всех симметричные отношений. При этом соотношение e14 • e5 = e13 вследствие ориентированности графа e13 приводит к тому, что граф e5 также оказывается ориентированным (так как граф e14 - неориентированный).
Таким образом, получаем Теорему:
Теорема 14. Система графов {ei} структурирована следующим образом: e0 - кольцо (точка), e1- e4, e7 - e11, e14, e15 - неориентированные графы (симметричные отношения, причем граф e14 является выделенным в плане состыкования между собой орбит, образованных действием асимметричных операторов), e5, e6, e12, и e13 - ориентированные графы (причем информация распространяется только по графам e13 и e5, а графы e12 и e6 ориентированы противоположно направлению распространения информации, - и поэтому могут рассматриваться как "информационные пробки"). Граф e1 является выделенным, т.к. его применение приводит к радикальной перестройке вектора представления типа.
СЛОВА из {ei} как цепочки выработки решений (цепочки распространения информации). Введенный выше формализм позволяет решать два класса задач.
· задачи об организации оптимального управления заданным типом 2-АИА с помощью некоего множества других 2-АИА (включая и тождественные типы 2-АИА), и
· задачи об организации выработки оптимального нового режима (способа, управления, алгоритма) для управления данным уровнем заданной ИСС.
Определение 11. Произвольную последовательность операторов из {ei} будем называть словом (последовательность применения операторов - справа налево).
Каждое такое слово задает цепочку выработки нового режима (способа, метода, алгоритма) для управления на данном иерархическом уровне в ИСС. Иначе говоря, каждое слово задает некую цепочку распространения новой информации.
Нетрудно видеть, что условия для оптимизации введенных выше задач будут разными.
Так, условие для оптимизации первойзадачи - по целенаправленному управлению деятельностью заданного 2-АИА с помощью некоторого множества других 2-АИА выглядит так:
Найти на множестве всех заданных 2-АИА слово минимальной длины, с минимальным количеством операторов, изменяющих рациональность и с минимальным количеством асимметричных операторов, которое заканчивается на заданном 2-АИА (часто при этом "начальный" 2-АИА задается также). Оптимальным является случай, когда асимметричный оператор e13 (или e5) стоит в конце слова (то есть - перед заданным 2-АИА).Наличие в слове операторов e12 и e6 означает наличие "информационной пробки", после которой информация дальше по слову не распространяется.
А условие для оптимизации второйзадачи - по выработке оптимального нового режима управления на данном множестве 2-АИА выглядит так:
Найти на множестве всех заданных 2-АИА слово максимальной длины, с минимальным количеством операторов, изменяющих рациональность и с максимальным количеством асимметричных операторов e13 и/или e5 (часто при этом "начальный" 2-АИА задается: именно через него, как правило, вводится новая информация в рассматриваемое множество 2-АИА). Оптимальным является случай, когда такое слово формирует замкнутый путь на рассматриваемом множестве 2-АИА (при выполнении такого условия тот 2-АИА, через который введена новая информация, осуществляет также "апробацию" выработанного нового режима управления, - то есть определяет, достигнуты ли цели управления и какова степень эффективности такого управления).
Замечание. Нетрудно видеть, что "общаться" между собой "на равных" могут только типы, обладающие одной и той же рациональностью. Действительно, иррациональный тип реализует управление "от общего к частному", тогда как рациональный тип - наоборот, "от частного к общему" (см. Теорему 14).
Весьма важным является то обстоятельство, что одно и то же слово может объединять в некоторый путь разные совокупности 2-АИА (особенно наглядно это при представлении операторов в виде графов).
Определение 12. Слова на множестве рассматриваемых типов 2-АИА будем называть эквивалентными в смысле передачи информации, если они опираются своими началом и концом на фиксированные типы 2-АИА (которые могут быть как разными, так и совпадающими, - в последнем случае получим цикл (кольцо) из 2-АИА).
Можно сказать, что слова - это топологически инвариантные конструкции на множестве {Тi}.
Таким образом, общий алгоритм решения задач по управлению данным уровнем ИСС произвольной природы с помощью некоего множества 2-АИА выглядит следующим образом.
1. На первом этапе определяются все типы 2-АИА, которые содержатся в рассматриваемом множестве 2-АИА.
2. На втором этапе определяются все типы операторов, которые связывают пары разных типов 2-АИА, содержащихся в рассматриваемом множестве 2-АИА.
3. Наконец, на третьем этапе выбираются слова, которые оптимальны для решения поставленной цели управления. Отметим, что цели управления в общем случае могут быть отличны от тех, которые перечислены выше: они будут определяться конкретным наполнением задачи на управление.
Таким образом, вместо того, чтобы исследовать цепочки передачи информации (цепочки выработки нового режима управления) между конкретными типами 2-АИА, теперь можно исследовать слова, которые являются инвариантными и не зависят уже от выбора конкретных типов.
Несколько вспомогательных конструкций. Сейчас рассмотрим некоторые конструкции, которые возникают на множестве всех типов 2-АИА {Тi} при условии максимально полной выработки нового режима управления. Иначе говоря, необходимо найти конструкцию, в которой задействованы все 16 типов 2-АИА и все 16 типов отношений между ними, и которая максимально приспособлена для выработки новых режимов управления.
Согласно алгоритму оптимизации для второй задачи - о выработке нового режима управления - такая конструкция должна содержать максимально большое количество замкнутых путей из асимметричных операторов.
Построим такую конструкцию
Данный тип 2-АИА (тот, который "ставит задачу" перед всеми остальными типами 2-АИА) формирует кольцо " индивидуального " самопрограммирования при помощи последовательного действия оператора e13.
Действие этого же оператора разбивает множество {Тi} еще на 3 кольца самопрограммирования. Только одно из таких колец индивидуального самопрограммирования может быть состыковано с данным типом 2-АИА с тем, чтобы образовать единое целое - кольцо сдвоенного (будем использовать для него название - " дуального ") самопрограммирования. Такое кольцо дуального самопрограммирования получится, если к данному типу 2-АИА присоединить при помощи оператора e14 соответствующий тип 2-АИА вместе с содержащим его кольцом индивидуального самопрограммирования.
Таким образом, множество {Тi} разбивается на два кольца дуального самопрограммирования, одно из которых содержит данный тип 2-АИА, а другое - нет.
Два кольца индивидуального самопрограммирования, которые составляют такое второе кольцо дуального самопрограммирования, можно присоединить к данному 2-АИА лишь только еще 4 разными способами: при помощи 4 разных операторов, не изменяющих рациональность типа. При этом присоединение происходит с теми типами, у которых либо программная, либо творческая функции совпадают с соответствующими функциями данного типа 2-АИА или типа, полученного из данного при помощи оператора e14 (такой тип называется " дуальным ").
При других способах присоединения колец индивидуального самопрограммирования к данному типу оптимальной передачи информации достигнуто не будет (так как информация будет искажаться при состыковании - коммуникации данного типа 2-АИА с другими типами 2-АИА).
Таким образом, получаем теорему:
Теорема 15. Конструкция на множестве типов 2-АИА {Тi}, которая оптимально способна преобразовать новую информацию, в топологическом смысле эквивалентна букету из 6 окружностей.
Следствие 1. Описанная в Теореме 15 конструкция диффеоморфна двумерной сфере с 7 вклеенными пленками Мебиуса (математические детали см., например, в[26]).
Определение 13. Введенную в Теореме 15 конструкцию будем называть соционом - такое определение совпадает с определением 9 из параграфа 1.2.
Нетрудно видеть, что в соционе для любого из типов 2-АИА присутствуют все возможные на множестве {Тi} операторы (отношения между типами). Таким образом, социон является объектом, содержащим наиболее длинное слово, в котором все типы 2-АИА из {Тi} присутствуют лишь один раз (наиболее длинный путь без повторов). В соционе реализован случай, когда отдельные 2-АИА осуществляют коммуникацию с наибольшим количеством других 2-АИА.
Итак, социон является как раз тем объектом, который должен быть образован для того, чтобы выработать всю совокупность возможных режимов (способов, алгоритмов, методов) для реализации управления данным уровнем в произвольной ИСС.
Замечание. Полученные в этом разделе результаты могут быть получены также "геометрическим" способом, когда соответствующие операторы представимы графами - как это было сделано выше в этом параграфе
Сети из {ei}. Как следует из построения социона, следующим шагом является построение сети из графов - представлений операторов {ei}. В этом случае придется оперировать объектами, являющимися разветвлениями графов - операторов: их можно представить как "точку (тип 2-АИА)", в которую "входит" n графов - операторов и из которой выходит m графов - операторов (в общем случае n¹m).
Построению соответствующего формализма будет посвящена отдельная работа (отметим, что здесь открываются широкие возможности для компьютерного моделирования и формирования объектов различного топологического строения и различной размерности - см., например[27]). Интересно, что, как следует из Теоремы 15, оптимальный для функционирование социона разветвленный граф может быть описан в виде объекта, в котором имеется 1 " вход " - асимметричный оператор, 1 " выход " - асимметричный оператор, и 5 неориентированных графа - симметричных оператора (нетрудно видеть, что любой 2-АИА может функционировать в составе социона лишь только тогда, когда на него опирается граф с 7±2 разветвлениями) - см. также Теорему 7.
Примеры приложений развитого формализма. Ниже описан один пример применения развитого выше формализм.
Нами также проведена апробация ряда слов для реализации управления. Например, уже год в одной из частных фирм для организации управления конкретным человеком - директором фирмы - применяется слово e13 • e4 - такое слово было предложено нами как оптимальное при анализе конкретного состава типов людей в данной фирме. Необходимость в таком управлении была вызвана тем обстоятельством, что типы нашего "заказчика" (человека, задающего управление) и директора фирмы связаны асимметричным отношением e6, то есть наш "заказчик" не имеет никакой возможности передать информацию своему директору (информация идет лишь только от директора к нашему "заказчику"). Интересно, что директор фирмы даже не подозревает, что он уже год "находится под управлением" (то есть управление происходит настолько "естественно", что он принимает его за... свои собственные решения). Отметим, что морально - этические аспекты этой проблемы нами были специально оговорены с нашим "заказчиком".
Крайне интересным представляется то обстоятельство, что множество разных слов для управления конкретными людьми имеет место, по нашим наблюдениям, среди ведущих Украинских политиков.
Подробнее эти аспекты описаны в парграфе 9.3.
Таким образом, получаем следующую Теорему:
Теорема 16. Векторы е0 - е15 задают ту же самую совокупность отношений между типами, которая описывается топологическим строением социона.
Следствие 1. 16 отношений между типами, описанные в настоящей книге, являются следствием способа определения типа и могут быть получены уже в рамках типологии Юнга-Майерс-Бриггс (так что можно только удивляться, почему для обнаружения этого и для их описания понадобилось почти полвека!).
Выводы:
1. Построено исчисление операторов, задающих отношения между парой типов режимов управления (парой 2-АИА) и описана структура множества таких операторов.
2. Описаны классы задач на оптимальное управление, которые решаются с применением введенного исчисления.
3. Описаны как общие методы решения задач на управление, так и некоторые характерные структуры из операторов, возникающие при этом, - результаты апробации свидетельствуют о высокой эффективности разработанных методов
1.5. Количественная модель для описания нормативных режимов общения между социальными группами и личностью
Дело в том, что одних наблюдений недостаточно: ими надо пользоваться, а для этого необходимо их обобщать. Так всегда и поступали; однако поскольку память о бывших ошибках делала человека все более осмотрительным, то наблюдать стали все больше, а обобщать все меньше.
А. Пуанкаре, "Наука и гипотеза"
В предыдущих параграфах мы рассмотрели эффекты, сопровождающие усвоение - социализацию новой информации, - то есть процесс выработки нового режима управления.
Вместе с тем ситуация, когда управление реализуется без необходимости в выработке новых режимов управления, - то есть когда уже имеющихся разработанных ранее режимов управления вполне достаточно для управления (например, когда мы встречаемся со стандартной ситуаций) - встречается довольно часто. Это не значит, что человеку при этом не приходится обрабатывать информацию, это не значит, что ему не приходится решать текущие задачи по управлению данным иерархическим уровнем. Это просто значит, что все необходимые режимы управления, все необходимые способы решения возникающих ситуаций - среди людей уже имеются, это значит - что каждый из рассматриваемых людей такие режимы управления уже знает, знаком с ними и научен им, - так что именно поэтому и не возникает необходимости в выработке чего-либо нового.
Итак, рассмотрим ситуацию, когда
· все люди обладают одинаковым набором способов управления Реальностью (то есть одинаковым набором знаний, умений, навыков и опыта), - и, в конечном счете, одинаковой информацией.
В этом случае тип от типа будет отличаться не количеством информации, а - "временем принятия решения", то есть каждый из типов будет просто иметь разное "время запаздывания" в реализации управления, разное "характерное время обработки данных".
Далее весьма кратко и схематично напомним некоторые сведения из нашей книги "Социальные Технологии...".. (Подробный вывод этой модели изложен именно в ней – см. http://soctech.narod.ru)
Построение модели
Итак, рассмотрим временные аспекты реализации управления каждым из типов при нормативном режиме управления, - то есть когда все типы обладают одинаковой информацией.
Прежде всего, опишем наиболее яркие и выразительные различия:
1) рациональный тип реагирует быстрее, чем иррациональный: ведь последний начинает действие лишь чтобы выйти из состояния - вот он и теряет время на "вхождение" в него. А рациональный тип реагирует сразу, "без раскачки": ведь он раньше уже продумал (!) использование всего, что ему известно (кроме того, временные промежутки, характеризующие конкретные КС значительно меньше, чем временные промежутки, которые характеризуют весь иерархический уровень как целое);
2) экстраверт реагирует быстрее, чем интроверт: ведь он программируется состоянием, тогда как интроверт - процессом, на распознавание которого теряется время;
3) логик реагирует быстрее, чем этик: ведь чтобы а) рациональному этику "рассмотреть" особенности взаимодействия между КС необходимо затратить больше времени, чем рациональному логику для анализа характеристик единственной КС, а б) иррациональный этик будет "раскручивать", "запускать" характеристики взаимодействия между КС большее время, чем иррациональный логик - делать то же, но для единственной КС;
4) сенсорик реагирует быстрее, чем интуит: как "увидеть", так и "сделать" характеристики мембраны можно быстрее, чем характеристики топологии.
Следует отметить, что все это верно лишь для типов, которые различаются лишь только одной из бинарных переменных!
С использованием вышесказанного легко получить следующую Таблицу для распределения типов на "плоскости времени":
® СЛЭ ЭИИ
¯ СЭЭ ЭСИ
ЭСЭ СЭИ
ЛСЭ ЭИЭ СЛИ ИЭИ
ЛИЭ ИЛИ
ЛИИ ИЛЭ
ЛСИ ИЭЭ
Стрелками указано направление времени.
Однако если мы имеем "время по вертикали" и "время по горизонтали", то закономерно возникает вопрос о том: а как же они связаны между собой? Более того: вся полученная таблица имеет смысл лишь только в том случае, когда имеется возможность рассчитать "время запаздывания" в принятии решений между любыми произвольно расположенными двумя типами. Для этого необходимо определение своего рода "расстояния", точнее - метрики на дискретном пространстве гнезд, соответствующих нашей таблице:
® i 2.1 5.1
¯ 3.1 4.1
k 2.2 5.2
1.1 3.2 4.2 6.1
2.3 5.3
3.3 4.3
2.4 5.4
Это будет именно метрика, а не расстояние, по той причине, что, например, Кi(1.2-2.2)=-Кi(2.2-2.1) (здесь Кi(А,В) - “рассто






