Процессы стирки и полоскания в машинах барабанного типа основаны на принципе динамического взаимодействия материальных систем, участвующих в относительном движении барабана. На каждую материальную точку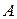 
белья массой 
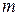(рис. 94) действуют силы: центростремительная, тяжести и инерции. В совокупности все эти силы определяют направление и характер движения данной материальной точки. Отношение центробежной силы 
к силе тяжести 
характеризуется критерием Фруда (фактором разделения):
,
где 
- угловая скорость вращения барабана; 
– расстояние от оси вращения до материальной точки.
Рис. 94. Силы, действующие на материальную точку во вращающемся барабане
Материальная точка массой 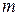приобретает относительное движение в барабане в сторону результирующего ускорения:
.
Движение материального потока (раствора и белья) зависит от угловой скорости барабана. Условно выделяют четыре режима [20]: лавинообразный при 
(рис. 95, а), лавиноводопадный при 
(рис. 95, б), водопадный (критический) при 
(рис. 95, в) и закритический при (рис. 95, г).
Рис. 95. Режимы движения материального потока при различных частотах вращения барабана:
а – лавинообразый; б – лавиноводопадный: 1 и 2 – восходящая и нисходящая ветви потока;
3 – разграничивающая зона; в – водопадный; г – закритический
Для стирки, полоскания задают лавиноводопадный режим движения. Он характеризуется тем, что в определенных точках пространства барабана происходит отделение частей белья и моющего раствора от общей массы и падение их в другую часть барабана. При этом происходит трение белья друг о друга, удар его о поверхность моющего раствора и интенсивное перемешивание. Различают две части потока: восходящую и нисходящую ветви.
Восхождение потока белья вместе с частью жидкости происходит из левого нижнего квадранта окружности барабана в левый верхний квадрант (рис. 96).
Рис. 96. Движение потока белья
Рассмотрим движение материальной точки потока 
относительно барабана, на поверхности которого она находится. Сила, стремящаяся придать точке скольжение, - составляющая силы тяжести:
,
где 
- угол подъема точки в нижнем квадранте.
Силе скольжения противодействует сила трения:
,
где 
– коэффициент трения; 
- радиус барабана.
Точка не будет скользить по барабану, пока 
, т.е. 
, или пока не будет достигнуто условие:
Если барабан неподвижен 
, то 
. Соотнеся 
с углом трения 
, получим:
.
Это означает, что при неподвижном барабане угол не может превысить угол трения 
. При вращающемся барабане и подъеме точки 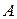выше горизонтального диаметра барабана 
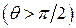ее положение будет характеризоваться углом 
. При этом на точку 
перестанет действовать составляющая силы трения от силы тяжести 
. Если угол 
таков, что 
, т.е.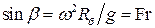 
, то тело в точке 
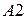будет падать в нижнюю часть барабана по параболе как свободное тело, брошенное со скоростью 
под углом к горизонту 
. Угол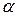 
называют при этом углом отрыва.
До наступления отрыва возможно движение точки с проскальзыванием. Оно наступает, когда угол достигает значения, определяемого по уравнению.
Из-за различия между коэффициентами трения движения 
и трения покоя 
формула дает два значения угла : 
и соответственно. Это означает, что во вращающемся барабане точка 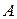поднимается на угол , затем начинает скользить вниз до положения . После этого процесс повторяется.
Движение точки 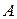в 
-м слое восходящего потока происходит при соответствующих значениях 
, 
, 
и 
. По уравнению можно сделать вывод, что угол по слоям восходящего потока – величина переменная, зависящая от скорости 
.
Относительная скорость скольжения двух смежных слоев 
вызывает взаимное трение белья в процессе стирки и полоскания.
Нисхождение потока характеризуется падением белья в нижнюю часть барабана. Траектория точки 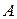белья представляет собой кривую 
, состоящую из двух ветвей: 
(подъем после отрыва от барабана со скоростью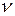 
) и 
(свободное падение).
Высоту 
ветви 
можно определить из уравнения движения тела 
, но 
, следовательно, время падения 
, где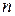 
, 
– частота вращения и диаметр рабочего барабана. Учитывая это уравнение, находим:
.
Отрыв белья от стенки барабана произойдет в момент, когда составляющая силы тяжести станет равной центробежной силе, т.е.:
.
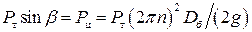С учетом данного равенства уравнение примет вид:
После некоторых преобразований найдем координаты точки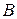 
падения белья:
.
Полная высота падения белья:
.
Величина 
достигнет максимума при условии:
0;
;
.
Мощность, необходимую для вращения барабана при стирке и полоскании, можно определить на основе следующей схемы (рис. 97).
Рис. 97. Схема для определения полезной мощности барабана
Масса белья, находящегося в жидкости внутри вращающегося барабана принимает форму, близкую к форме цилиндрического сегмента 
. Центр тяжести сегмента (точка 
) смещается в сторону вращения. Полезный момент силы сопротивления вращению барабана:
,
где 
- сила тяжести массы изделий и жидкости в барабане;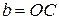 
расстояние от оси вращения барабана до центра тяжести белья и жидкости в барабане; - угол поворота сегмента.
Масса мокрого белья в барабане:
,
где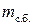 
- масса сухого загружаемого белья; 
- масса жидкости, впитанной бельем (для воды и водных моющих растворов в тканых изделиях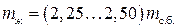 
.
Масса жидкости, увлекаемой бельем при вращении барабана:
.
Общая масса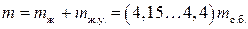 
.
Объем, занимаемый мокрым бельем и свободной жидкостью:
,
где 
- плотности сухого белья и жидкости соответственно.
Обычно принимают 
.
Тогда 
Положение центра тяжести сегмента находится из геометрических соотношений:
,
где 
- длина хорды сегмента;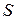 
- площадь сегмента.
Площадь сегмента - это часть площади поперечного сечения барабана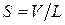 
, где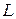 
- длина барабана.
Длина хорды связана с центральным углом сегмента 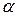через радиус барабана : 
, а угол 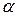находится из соотношения: 
.
Из формулы получим:
Угловую скорость следует задавать так, чтобы при лавиноводопадном режиме обеспечить наибольшую высоту падения отделившихся от основной массы частей белья. Этому соответствует угол отрыва . Из соотношений 
и 
определим оптимальную угловую скорость барабана при стирке и полоскании:
.
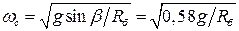Подставив значения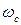 
и других параметров в формулу, определим .
Мощность на валу барабана для преодоления полезного сопротивления должна составлять:
,
где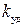 
– коэффициент, учитывающий неравномерность полезной нагрузки вследствие падений и ударов белья внутри барабана 
Мощность для преодоления силы трения в подшипниках:
где 
– коэффициент трения в подшипниках (для шарикоподшипников 
); 
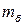- масса барабана (
, кг); 
- вектор силы натяжения ремня привода (
Н).
В период пуска барабана необходима дополнительная мощность:
- на подъем центра тяжести сегмента: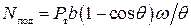 
;
- на преодоление сил инерции масс барабана, белья и жидкости при разгоне барабана: 
, где 
- моменты инерций массы барабана и массы белья и жидкости 
; 
); 
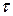- время разгона.
Если принять, что разгон барабана совершается за половину оборота, то:
.
Полная мощность при стирке и полоскании:
.
