Таблица 1.2 – Результаты оценки выигрыша в точности
| Измерительный канал | 
| 
| 
| 
| 
| 
| 
|  , %
|
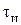
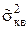
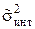
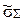| Неоптимизированный канал | ||||||||
| Оптимизированный канал |
Опыт 2. Изучение влияния запаздывания измерительной информации на выбор оптимальных параметров цифровой системы передачи
Использование измерительной информации для управления объектом в реальном масштабе времени требует учета ее задержки. Погрешность запаздывания существенно возрастает при увеличении степени интерполирующего полинома. В настоящем опыте исследуется влияние учета запаздывания сигнала на результирующую погрешность измерительного канала и его оптимальные параметры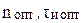 
при линейной интерполяции.
Порядок выполнения опыта
1 Запустить программу расчета оптимальных параметров измерительного канала.
2 Ввести заданные руководителем исходные данные при линейной интерполяции и учете запаздывания измерительной информации. Результаты расчета оптимизированной системы занести в табл. 1.3.
3 Запустить программу на выполнение с теми же исходными данными, но без учета запаздывания. Занести результаты расчета параметров оптимизированной системы в табл. 1.3.
Таблица 1.3 – Оценка влияния запаздывания измерительной информации
на выбор оптимальных параметров
| Измерительный канал | 
| 
| 
| 
| 
| 
| 
|  , %
|
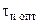
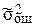
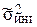
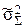
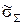| С учетом запаздывания | ||||||||
| Без учета запаздывания |
4 Сделать вывод о влиянии погрешности запаздывания на выбор оптимальных параметров проектируемой цифровой системы передачи измерительной информации.
Опыт 3. Выбор степени интерполирующего полинома
В данном опыте рассматривается оптимизированная цифровая
система передачи аналоговых сигналов, восстановление которых на приемной стороне осуществляется с помощью интерполяционного полинома Лагранжа нулевой или первой степени. Выбор степени полинома должен производиться из условия обеспечения минимальной результирующей погрешности измерительного канала. Сравнение способов интерполяции следует проводить с учетом запаздывания информации.
Порядок выполнения опыта
1 Запустить на выполнение программу расчета оптимальных параметров.
2 Ввести исходные данные, заданные руководителем, при использовании линейной интерполяции. Полученные для оптимизированного канала результаты занести в табл. 1.4.
3 Повторно запустить программу с теми же исходными данными, но при ступенчатой интерполяции. Результаты расчета для оптимизированного канала свести в табл. 1.4.
Таблица 1.4 – Оценка влияния степени интерполирующего полинома
на выбор оптимальных параметров
| Степень интерполирующего полинома |
| 
|
|
| 
|
| 
|  , %
|
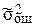
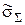4 Сделать вывод о выборе степени интерполирующего полинома.
Опыт 4. Изучение зависимости оптимальных параметров системы от характеристик канала связи и входного сигнала
Как следует из выражения (1.8), результирующая погрешность измерительного канала зависит от частоты среза 
входного сигнала и энергетического параметра 
канала связи. При заданных значениях скорости модуляции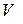 
и вероятности трансформации символа в канале связи 
, отношение мощности сигнала к спектральной плотности шума можно вычислить по следующей формуле:
.
Порядок выполнения опыта
1 Рассчитать значения энергетического параметра для вероятности 
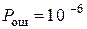и скоростей модуляции 
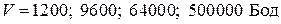. Полученные значения занести в табл. 1.5.
2 Запустить на выполнение программу расчета оптимальных параметров, ввести заданные руководителем исходные данные для системы с линейной интерполяцией, учетом запаздывания информации,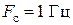 
, 
, 
.
3 Результаты расчета оптимальных параметров занести в табл. 1.5.
4 Повторить запуск программы для тех же исходных данных и значений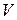 
, указанных в п. 1, свести результаты в табл. 1.5.
Таблица 1.5 – Зависимость оптимальных параметров от характеристик
канала связи
; 
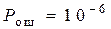
| Оптимизируемый параметр | Энергетический параметр 
| |||
при 
| при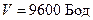 
| при 
| при 
| |
| ||||
| ||||
 , %
|
Запустить программу на выполнение для системы с линейной интерполяцией, учетом запаздывания, 
, 
при частотах среза 
. Оптимальные значения параметров занести в табл. 1.6.
Таблица 1.6 – Зависимость оптимальных параметров от характеристик
входного сигнала
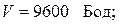
| Оптимизируемый параметр | Частота среза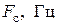 
| |||
| 0.1 | ||||
|
| ||||
|
| ||||
 , %
|
1 Построить графики зависимостей 
и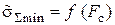 
. Значения 
на графиках откладывать в логарифмическом масштабе.
2 Проанализировать зависимость оптимизируемых параметров системы от характеристик входного сигнала и условий передачи в канапе связи. Сформулировать рекомендации по построению адаптивных систем.
Содержание отчета
1 Модель измерительного канала (см. рис. 1.1).
2 Аналитическое выражение (1.8) критерия качества системы.
3 Табл. 1.2 – 1.6 с результатами опытов.
4 Графики зависимостей 
и 
.
5 Краткие выводы.
Контрольные вопросы
1 Область применения цифровых способов передачи аналоговых сигналов.
2 Преимущества цифровых методов передачи.
3 Статистическая модель измерительного канала.
4 Критерий качества цифровой системы передачи измерительных сигналов. Составляющие результирующей погрешности. Их аналитические выражения с учетом принятых ограничений.
5 Методика оптимизации измерительного канала.
6 Влияние погрешности запаздывания на выбор оптимальных параметров канала.
7 Обоснование выбора способа интерполяции.
8 Зависимость оптимальных параметров системы от частоты входного сигнала и отношения сигнал/шум в канале связи.
Список рекомендуемой литературы
1. Оптимизация систем цифровой передачи измерительных сигналов: Учеб. пособие / Терентьев С.Н., Глухов А.Б., Константинова Л.В. – Харьков НТУ «ХПИ», 2002. – 268 с.
2. Новоселов О.М., Фомин А.Т. Основы теории и расчета информационно-измерительных систем / Под ред. А.В. Фремке. – М.: Машиностроение, 1960. – 280 C.
Лабораторная работа №2
