ВСТУПЛЕНИЕ
Одной из важнейших проблем при создании информационно-измерительных систем (ИИС) является разработка методов повышения верности передачи аналоговых измерительных сообщений по дискретным каналам связи. Существенной особенностью каналов преобразования и передачи количественной информации является повышенное требование к их точностным характеристикам.
Настоящие методические указания содержат описание четырех лабораторных работ, в которых рассматриваются принципы построения измерительных каналов ИИС и изучаются их основные характеристики.
В первой лабораторной работе на основе анализа статистической модели канала преобразования и передачи измерительной информации и зависимостей погрешностей от основных параметров измерительного канала и характеристик входного сигнала рассматривается методика оптимального по критерию точности выбора параметров ИИС.
Вторая лабораторная работа посвящена изучению кодов Хемминга и оценке целесообразности их использования в зависимости от условий в канале связи.
В третьей работе приводится анализ помехоустойчивости некогерентного приема по огибающей узкополосного процесса. Исследуются преобразования законов распределения случайных процессов типовыми звеньями радиотехнических устройств. Изучается аппаратурный метод измерения плотности распределения вероятностей.
Четвертая работа посвящена анализу помехоустойчивости оптимального способа приема, реализованного на основе согласованного фильтра приемника.
Темы лабораторных работ представляют интерес для будущей практической деятельности выпускников и соответствуют программе курса «Информационно-измерительные системы» для студентов специальности «Метрология и измерительная техника».
Лабораторная работа №1
ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ ИЗМЕРИТЕЛЬНОГО КАНАЛА ПО КРИТЕРИЮ ТОЧНОСТИ
Цель работы – изучение статистической модели канала преобразования и передачи измерительной информации, углубление теоретических знаний в области расчета погрешностей измерительных каналов, исследование зависимости оптимальных параметров цифровых систем передачи аналоговой информации от выбора структуры измерительного канала, характеристик входного сигнала и условий передачи в канале связи.
Опыт 1. Изучение модели измерительного канала. Параметрическая оптимизация цифровой системы передачи измерительной информации по критерию точности
В работе исследуется измерительный канал, лежащий в основе цифровой системы передачи измерительной информации, которая в свою очередь является частью территориально рассредоточенной автоматизированной информационно-управляющей системы. Для достижения высокой точности управления необходимо обеспечить высокую точность преобразования и передачи измерительных сигналов. При этом следует иметь в виду, что задержка информации, использующейся для целей управления, равносильна потере точности.
Цифровые методы передачи измерительной информации получили широкое распространение в таких областях, как автоматизация технологических процессов производства, в системах телеизмерения и телеуправления подвижными объектами, летательными аппаратами и в ряде других областей – всюду, где на основании измерительной информации необходимо судить о поведении объекта и вырабатывать управляющие воздействия.
Хорошо известные преимущества цифровых методов передачи аналоговых сигналов (а к ним относится большинство измерительных) привели к тому, что в настоящее время практически все системы передачи измерительной информации являются цифровыми. Цифровые системы обеспечивают высокую эффективность и помехоустойчивость передачи сигналов, совместимость каналов различных типов, а также возможность построения аппаратуры на перспективной элементной базе, что повышает надежность устройств и улучшает их эксплуатационные и экономические показатели.
Описать процесс преобразования и передачи измерительного сигнала, выбрать критерий качества системы целесообразно с помощью модели, учитывающей основные источники погрешностей. Модель канала преобразования и передачи измерительной информации представлена на рис. 1.1. Аналоговый сигнал 
квантуется по времени и уровню, преобразуется в цифровой код. Передающее устройство превращает элементы цифрового кода в сигналы. При примитивном кодировании эта процедура сводится к модуляции, а при помехоустойчивом еще и к дополнению контрольными символами. Затем сигнал передается по каналу связи, где подвергается воздействию аддитивной помехи. В приемном устройстве по принятым колебаниям принимаются решения о том, каким из возможных значений кодовых символов они соответствуют. Из-за искажающего действия помех принятые сигналы в общем случае могут не совпадать с переданными. В декодере принятые цифровые символы кодового слова преобразуются в дискретную величину. Интерполятор осуществляет переход от дискретного представления процесса к непрерывному.
В соответствии с назначением системы целесообразно выбрать критерий качества в виде среднего риска с квадратичной функцией потерь. Этот критерий можно рассматривать как дисперсию результирующей погрешности, основными составляющими которой являются: погрешность квантования измерительного сигнала по уровню, погрешность в передаче квантованных значений сигнала по цифровому каналу связи, погрешность восстановления аналоговой формы сигнала на приемной стороне, погрешность запаздывания за счет аналого-цифрового преобразования, интерполяции и декодирования. Существенным здесь является то, что моделью учитывается погрешность, возникающая в результате запаздывания измерительного сигнала.
Модель не учитывает погрешности датчиков, инструментальные погрешности преобразователей, не влияющие на оптимизируемые параметры системы.
При определении результирующей погрешности сделано допущение о статистической независимости ее составляющих. Основанием для этого может служить рассмотрение физической сущности процессов преобразования с учетом принятых конкретных способов дискретизации и квантования.
Для определенности принято:
квантование входного сигнала по уровню и дискретизация по времени равномерные, сообщение представляется регулярными выборками с периодом 
;
передача в бинарном канале осуществляется частотно-модулированным сигналом, прием – посимвольный, некогерентный;
кодирование в канале безызбыточное, 
– значным равномерным кодом;
при аналого-цифровом преобразовании аналоговое значение сигнала запоминается на время преобразования;
кодовая комбинация передается за время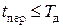 
.
Принятые условия позволяют записать аналитические зависимости составляющих результирующей погрешности, выраженные через параметры системы.
Известно, что погрешность квантования определяется из выражения
, (1.1)
т.е. приведенная дисперсия погрешности квантования 
зависит только от 
– разрядности кодовых чисел.
Здесь и в дальнейшем приведенное значение дисперсии определяется как отношение дисперсии погрешности к квадрату максимального значения входного сигнала.
Погрешность от трансформации символов в канале связи при поэлементном некогерентном приеме
, (1.2)
где 
– отношение мощности сигнала к спектральной плотности шума в канале связи; 
– длительность канального импульса. Таким образом, при заданных условиях в канале связи приведенная дисперсия погрешности передачи зависит только от длительности импульсов .
Обобщенные выражения дисперсий погрешностей интерполяции и запаздывания получены для трех наиболее часто встречающихся видов корреляционной функции входного сигнала:
1) 
;
2) 
;
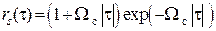3) 
.
При восстановлении входного процесса по дискретным выборкам с помощью интерполяционного полинома Лагранжа, который является наиболее простым в технической реализации и для достаточно широкого класса сигналов дает приемлемую точность,
, (1.3)
где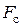 
– верхняя граничная частота спектра входного сигнала; коэффициент 
и показатель степени 
зависят от вида корреляционной функции измерительного процесса и степени интерполирующего полинома. Из последнего выражения следует, что при заданных характеристиках входного сигнала и способе восстановления аналогового сигнала приведенная дисперсия погрешности интерполяции 
зависит от частоты дискретизации 
входного процесса.
При частотном уплотнении линии связи и использовании времени полностью для передачи двоичного числа
. (1.4)
Для указанных выше корреляционных функций дисперсия погрешности запаздывания
, (1.5)
где коэффициент 
и показатель степени 
определяются видом корреляционной функции измерительного сигнала; 
– время запаздывания, определяющееся при линейной интерполяции выражением
, (1.6)
где 
– параметр быстродействия АЦП (время преобразования одного разряда), при ступенчатой интерполяции восстановление аналоговой формы сигнала не требует задержки, тогда
, (1.7)
т.е. при заданных параметрах входного сигнала и степени интерполирующего полинома приведенная дисперсия погрешности запаздывания зависит только от разрядности двоичных чисел и длительности кодового импульса.
С учетом выражений (1.1 – 1.7) приведенная дисперсия результирующей погрешности может быть записана в виде:
, (1.8)
где 
– степень интерполирующего полинома.
В табл. 1.1 приведены значения величин 
, позволяющие записать выражения результирующей погрешности для каналов с различной структурой.
Таблица 1.1 – Значения величин 
| Корреляционная функция входного сигнала | Структура канала |
| 
|
| 
|
| линейная интерполяция с учетом запаздывания ступенчатая интерполяция с учетом запаздывания линейная интерполяция без учета запаздывания | 0,5818·10–1 0,8727·10–1 0,5818·10–1 | 0,3491 0,3491 | – | |
| линейная интерполяция с учетом запаздывания ступенчатая интерполяция с учетом запаздывания линейная интерполяция без учета запаздывания | 0,3062 0,9139·10–1 0,3062 | 0,2647·101 0,2647·101 | – | |
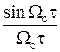
| линейная интерполяция с учетом запаздывания ступенчатая интерполяция с учетом запаздывания линейная интерполяция без учета запаздывания | 0,7215·10–1 0,3046·10–1 0,7215·10–1 | 0,3655 0,3655 | – |
Анализ составляющих результирующей погрешности показывает, что все они противоречивым образом зависят от двух параметров цифровой системы передачи – числа разрядов кодового слова 
и длительности импульсов в канале связи 
. Таким образом, задача минимизации результирующей погрешности сводится к двумерной вариационной задаче, исходными данными для которой с учетом принятых ограничений являются: вид корреляционной функции, ширина частотного спектра измерительного сигнала, быстродействие АЦП, способ интерполяции и отношение сигнал/шум в канале связи. В результате решения задачи находятся: комбинация оптимальных параметров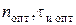 
и соответствующее им значение результирующей погрешности.
Доказанная в [1] единственность решения позволяет перейти от двумерной задачи к одномерной и произвести перебор вариантов. В результате предложен следующий порядок решения вариационной задачи:
1) для заданных 
из условия 
определяются значения 
;
2) по формуле (1.8) вычисляются значения 
при 
и ;
3) находятся оптимальные 
и 
.
Блок-схема алгоритма, реализующего предложенный способ оптимизации, приведена на рис. 1.2. Разработанная на его основе программа служит для определения оптимальных значений 
, минимального значения результирующей погрешности 
и ее составляющих, оценки выигрыша в точности от оптимизации.
Порядок выполнения опыта
1 Запустить программу Монитор.
2 Запустить программу Бейсик.
3 Загрузить программу расчета оптимальных параметров измерительного канала.
4 Запустить программу на выполнение, ввести заданные руководителем исходные данные.
5 Просмотреть результаты вычислений и занести результаты в табл. 1.2. Дать сравнительную оценку составляющих результирующей погрешности измерительного канала.
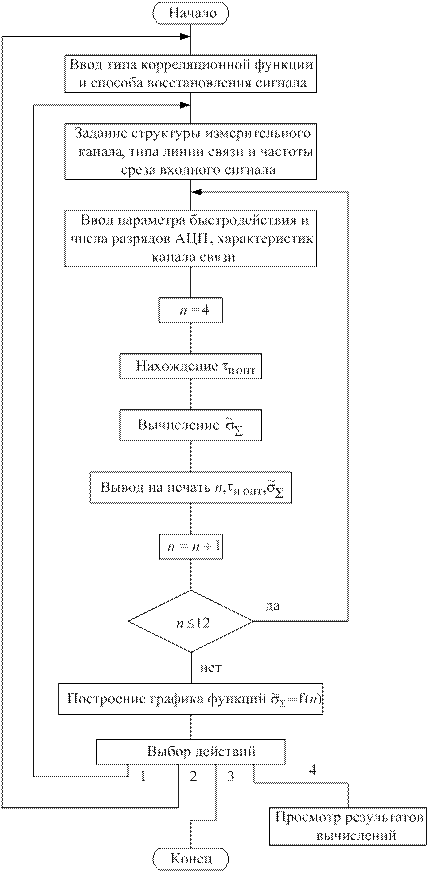
Рисунок 1.2. – Блок-схема алгоритма определения оптимальных
