Качество электрической энергии вместе с надежностью электроснабжения и его экономичностью является важнейшим требованием, предъявляемым к производству и передаче электроэнергии потребителям. ПКЭ регламентированы специальным техническим законом ГОСТ 13109-97.
Одним из основных показателей качества электрической энергии являются отклонения напряжения на зажимах электроприемников от номинального значения. Влияние уровня подведенного напряжения на производительность механизмов, освещенность помещений, надежность и долговечность эксплуатации электрооборудования общеизвестно.
В связи со случайным характером нагрузок отдельных участков электрической сети и большим количеством нагрузок полноценный анализ качества напряжения возможен только вероятностно-статистическими методами. Вероятностными методами можно решать такие задачи как выбор мест установки регулирующих устройств, выбор диапазонов и ступеней регулирования напряжения, выбор мощности, место установки и режимов работы компенсирующих устройств.
Статистический метод дает возможность охарактеризовать суммарное воздействие всех влияющих факторов на исследуемую величину отклонения напряжения с помощью интегральных критериев, учитывающих величину отклонения, продолжительность отклонения и вероятность появления того или иного отклонения с определенной продолжительностью.
Случайной называют функцию у = f(х), которая в результате опыта принимает некоторое заранее неизвестное значение. Каждое такое значение называют реализацией случайной функции, а все полученные реализации данной случайной функции составляют ансамбль реализаций. Случайные функции, непосредственно зависящие от времени, называют случайными процессами.
Процесс называется стационарным, если его вероятностные характеристики инвариантны во времени, т. е. например его математическое ожидание имеет приблизительно постоянную величину, которая сохраняется независимо от начала отсчета времени.
Важнейшим свойством случайных процессов является свойство эргодичности. Эргодичность позволяет перейти от усреднения по ансамблю реализаций к усреднению по времени для одной реализации. Например, математическое ожидание эргодического процесса можно найти не только как предел бесконечной последовательности среднеарифметических значений множества реализаций, но и как среднеарифметическое значение ординат развернутой реализации при стремлении времени усреднения к бесконечности. Это свойство имеет очень большое практическое значение, так как позволяет распространить характеристики, полученные для одной системы на все остальные системы, где наблюдается данный случайный процесс. Это значительно упрощает исследование, т. к. оно связано с накоплением статистических данных, получаемых, например, с помощью самопишущего прибора в серии экспериментов.
Статистический анализ заключается в определении основных вероятностных характеристик процесса. Он может быть произведен как на основе обработки имеющейся реализации, так и непосредственно подключением на вход прибора напряжения, отражающего исследуемый случайный стационарный процесс. В последнем случае чаще всего анализаторы используются для определения плотности распределения вероятностей j(v) случайной величины v - отклонения напряжения от номинального.
Плотность распределения является кривой, позволяющей судить о количестве случаев отклонений напряжения в диапазоне (v 2- v 1) или о вероятности (времени) отклонения напряжения в пределах этого диапазона (рис. 1, а). Получение и обработка непрерывной кривой распределения затруднительны. Поэтому данные целесообразно группировать и представлять в виде гистограммы (рис. 1, б), заменяющей кривую. Диапазон изменения величины в этом случае разбит на ряд интервалов (разрядов) одинаковой ширины D v, которым соответствуют различные вероятности величин в этих интервалах.
Для решения практических задач применяют числовые методы, используя числовые характеристики случайных величин. Они представляются так называемыми моментами: начальными и центральными. Начальные моменты могут быть представлены выражением
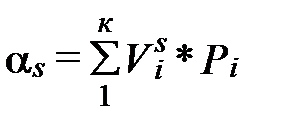 , (1)
, (1)
где Vi – отклонение напряжения в i –й момент измерения; Pi - вероятность появления этого отклонения; К – число разрядов; S - показатель степени, характеризующий порядок момента.
Наиболее важным из начальных моментов является первый начальный момент или математическое ожидание. При достаточно большом числе измерений вычисленное среднее арифметическое отклонение напряжения приближается к величине математического ожидания М (v) и его значение может быть определено из выражения
| j(V) |
| a) |
| V 1 |
| V 2 |
| б) |
| V 1 |
| V 2 |
| V 2 – V 1 |
| D V |
| Pi |
| Рис. 1. Кривая плотности распределения (а) и гистограмма отклонения напряжения (б) |
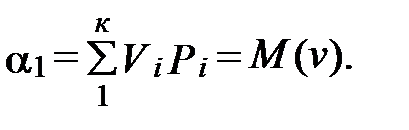 (2)
(2)
Второй начальный момент отклонения напряжения называют «неодинаковостью» и обозначают
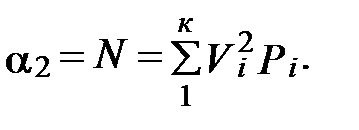 (3)
(3)
Центральные моменты могут быть представлены выражением
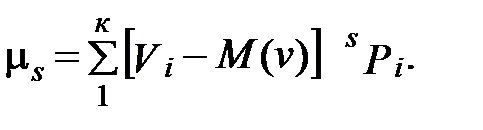 (4)
(4)
Во многих случаях качество напряжения достаточно полно характеризуется моментами первого и второго порядка. Центральный момент первого порядка используется редко. Чаще всего применяется второй центральный момент, характеризующий рассеяние случайной величины от ее математического ожидания и который называют дисперсией
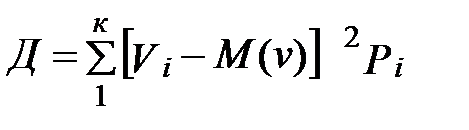 . (5)
. (5)
Часто рассеяние характеризуется стандартным отклонением или стандартом. Стандартом называется среднеквадратическое отклонение случайного процесса от среднего значения (среднеквадратическое отклонение функции V (t) от среднего уровня). Стандарт связан с дисперсией и «неодинаковостью» напряжения соотношениями:
 (6)
(6)
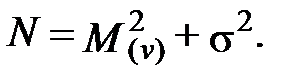 (7)
(7)
Все основные вероятностные характеристики случайного стационарного процесса могут быть вычислены по имеющейся гистограмме распределения отклонений напряжений.






