Цель работы:
1. Уяснение цели повышения коэффициента мощности на предприятии.
2. Исследование влияния нагрузки электрооборудования на значение коэффициента мощности.
3. Исследование влияния установки компенсирующих устройств на величину тока в питающей линии.
4. Исследование зависимости потребления реактивной мощности асинхронного двигателя от его загрузки.
В цепях синусоидального тока, содержащих активное сопротивление r и индуктивность L, различают три вида мощности: активную – Р, реактивную – Q и полную (кажущуюся) мощность – S, равную произведению действующих значений тока – I и напряжения – U.
S = U × I. (1)
Разложив вектор тока на две составляющие: активную – Ia = I × cos j, совпадающую по фазе с напряжением U, приложенным к цепи; и реактивную – Ip = I × sin j, отстающую от напряжения на 90о, выражение (1) примет вид
(2)
Обозначив произведение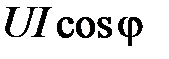 
через Р, а 
через Q, получим
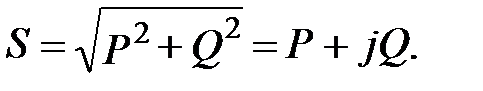(3)
Первая составляющая в (3) называется активной мощностью и расходуется на выполнение приемником полезной работы. Выясним сущность второй составляющей Q, называемой реактивной мощностью.
Полагаем, что приемник электрической энергии присоединен к источнику синусоидального напряжения 
и потребляет из сети синусоидальный ток 
, сдвинутый по фазе относительно напряжения на угол j.
Значение мгновенной мощности на зажимах приемника определится
Используя тригонометрическую формулу
получим
(4)
Таким образом, мгновенная мощность переменного тока может быть представлена в виде суммы постоянной величины P = UI cos j, не зависящей от времени, и синусоидальной q = UI cos(2 wt + j), изменяющейся с двойной (по сравнению с током и напряжением) частотой (рис. 1). Сравнивая (3) и (4), находим, что первый член характеризует активную мощность, а второй – реактивную.
| Рис. 1. График изменения напряжения, тока и мощности индуктивной нагрузкой |
Средняя за период Т мощность Р может быть определена по формуле
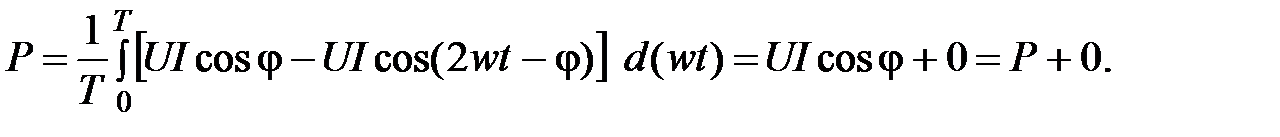(5)
Среднее значение от второго слагаемого мгновенной мощности в (5) равно нулю, т. е. ее создание не требует каких-либо материальных затрат и поэтому она не может совершать полезной работы, а лишь показывает, что между генератором и электроприемником происходит периодический обмен энергией без преобразования ее в другой вид (механическую или тепловую).
Следовательно, реактивная мощность служит лишь для создания магнитных полей в индуктивных электроприемниках.
Хотя на создание реактивной мощности не требуется расхода электроэнергии, тем не менее протекание этой мощности во всех звеньях схемы питания вызывает нежелательные потери напряжения D U, потери активной мощности D Рр и электроэнергии и излишне загружает генераторы электростанций и сеть реактивными токами, что видно из выражений (для 3-х фазного тока)
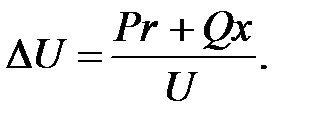(6)
(7)
(8)
До недавнего времени основным нормативным показателем, характеризующим реактивную мощность, был коэффициент мощности
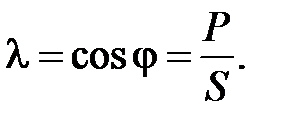(9)
Выражение (9) справедливо при синусоидальном токе. Для нагрузки, потребляющей несинусоидальный ток, например, вентильных преобразователей коэффициент мощности равен
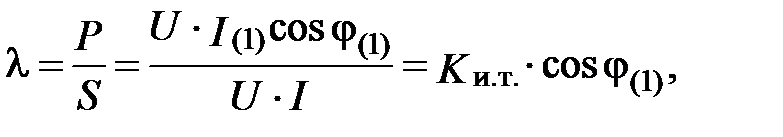(10)
где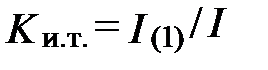 
– коэффициент искажения тока, 
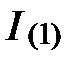– ток основной гармоники, I – действующее значение полного тока в учетом высших гармоник, равно
Но выбор cos j в качестве нормативного не дает четкого представления о динамике изменения реального значения реактивной мощности. Поэтому в настоящее время чаще пользуются значением tg j = Q/P, которое назвали коэффициентом реактивной мощности.
Связь между D P и tg j (cos j) можно найти, разделив (8) на Р2. Тогда полные потери мощности на передачу одного (кВт)2 активной мощности будут равны
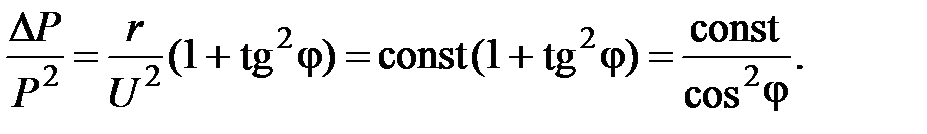(11)
Следовательно, удельные потери на передачу (1 кВт)2 обратно пропорциональны 
, в реактивная составляющая потерь на (1 кВт)2 прямо пропорциональна 
. Поэтому поведение cos j (или уменьшение tg j) является важной народно-хозяйственной задачей, так как позволяет экономить электроэнергию, высвободить мощности генераторов на электростанциях, экономить топливо, увеличить пропускную способность ЛЭП.
Как видно из выражения (11), уменьшить удельные потери на передачу, не изменяя сечения ЛЭП (r = const) и напряжения U, можно разными способами: 1) увеличить загрузку линии или электроприемника по активной мощности при Q = const; 2) уменьшить передаваемую реактивную мощность по сети.
Оба эти способа используются на практике. Это, во-первых, правильная эксплуатация электрооборудования (правильный выбор электродвигателей по мощности и типу); замена недогруженных двигателей, установка ограничителей холостого хода и т. п.; во-вторых, установка источников реактивной мощности (ИРМ) на месте потребления – так называемая компенсация реактивной мощности.
Простым и наиболее распространенным компенсирующим устройством является батареи статических конденсаторов, у которых ток опережает напряжение на 90о (БК). Реактивная мощность БК определяется из выражения
(12)
где Q к – кВар, w = 2p f = 314 (при f = 50 Гц), U – кВ, С – емкость БК, мкФ.
Необходимую мощность компенсирующего устройства Q к определяют расчетным путем по формуле
(13)
где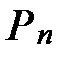 
– мощность, потребляемая предприятием, электроприемником, 
– тангенсы углов до компенсации и после компенсации.
Долевое участие отдельных электроприемников в общем балансе реактивной мощности, потребляемой промышленными предприятиями, таково: асинхронный двигатели – 60 %, трансформаторы – 20 %, преобразователи, реакторы, электрические сети и прочие электроустановки – 20 %.
Поэтому асинхронный двигатель может служить моделью системы электроснабжения промышленного предприятия с точки зрения потребления реактивной мощности. В этой работе моделью системы электроснабжения промышленного предприятия служит асинхронный двигатель.
Задание
1. Ознакомиться с лабораторной установкой, схемой и провести исследования, указанные в разделе «Цель работы».
Паспортные данные электродвигателя: Р н = 1,0 кВт; U н = 380 В; I н = 2,4 А; cos j = 0,79; h = 78,5%; n н = 1450 об/мин.; I пуск = 5 × I н.
2. Опытным путем определить зависимость потребления реактивной мощности из сети при различной загрузке двигателя, которая характеризуется коэффициентом b, равным
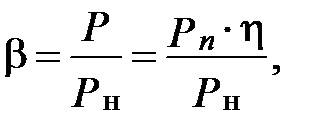
где Р – мощность, развиваемая двигателем на валу; Р н – номинальная мощность двигателя; Рn – мощность, потребляемая двигателем из сети при нагрузке на валу, равной Р
где h – КПД двигателя при нагрузке на валу, Р – определяется из графика (рис. 2).
| Рис. 2. Зависимость КПД от мощности, потребляемой из сети |
3. Провести улучшение (увеличение) cos j двигателя путем параллельного подключения конденсаторов, записывая показания приборов в таблицу и построить графики зависимостей 
до и после компенсации, а также 
до и после подключения конденсаторов.
4. Сделать выводы по работе.
