Цель работы: изучение распределения потока тепловых нейтронов в элементарной ячейке реактора с использованием моделирования на электрической сеточной модели
Теоретические основы
Распределение потока тепловых нейтронов в элементарной ячейке гетерогенного реактора достаточно хорошо описывается одногрупповыми диффузионными уравнениями:
в замедлителе –
, (1)
в топливе –
, (2)
где DM и DF – коэффициенты диффузии в замедлителе и в топливе; 
и 
– сечения поглощения нейтронов в замедлителе и в топливе; q – плотность замедления при тепловой энергии.
Граничные условия для системы (1) и (2) записываются следующим образом:
на границе топлива и замедлителя –
; (3)
на границе ячейки –
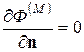, (4)
где n - нормаль к границе ячейки.
При расчете ячейки применяют метод эквивалентной ячейки, в котором производится переход от реальной геометрической формы ячейки к цилиндрической. Если затем решить уравнения (1) и (2) для двухзонной эквивалентной ячейки, то для распределения нейтронного потока в блоке горючего и в замедлителе получается следующие:
, (5)
, (6)
где RF – радиус блока горючего, RM – радиус эквивалентной ячейки, 
, 
.
Деформация ячейки в методе эквивалентной ячейки приводит к искажению действительной картины распределения нейтронного потока в замедлителе и, следовательно, к определенной погрешности при вычислении коэффициента использования тепловых нейтронов. Погрешность эта становится существенной для «тесных» решеток. С определенными затруднениями связан расчет ячеек сложной формы, многозонных, со сборками ТВЭЛ.
Моделирование на электрической сеточной модели позволяет сравнительно легко получить распределение нейтронного потока в ячейке реальной формы.
Для того, чтобы использовать уравнения (1) и (2) в сеточной модели, их нужно предварительно преобразить в конечно-разностную форму и перейти к безразмерным функциям 
и 
. Для узлов (i, k) в замедлителе и (j, l) в блоке горючего эти уравнения запишутся следующим образом (см. рис. 1):
, (7)
, (8)
где 
– безразмерный поток нейтронов; 
– базисное значение потока, hM и hF – шаг сетки в замедлителе и топливе.
Моделирующее устройство и выбор параметров элементов этого устройства. Для решения уравнений (7) и (8) применяется специализированное вычислительное устройство, содержащее электрическую сеточную модель из двух типов ячеек (рис. 2).
 |
Первый тип ячейки (рис. 2а) применяется для моделирования распределения нейтронного потока в замедлителе. Токи в сопротивлениях RM моделируют диффузию в замедлителе, в сопротивлениях
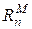– поглощение нейтронов, в сопротивлениях 
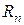– источники тепловых нейтронов.
Ячейки второго типа (рис. 2б) предназначены для моделирования распределения нейтронного потока в топливе. Токи в сопротивлениях 
моделируют диффузию в топливе, в сопротивлениях 
– поглощение нейтронов.
Потенциалы узловых точек сетки 
пропорциональны величинам нейтронного потока 
в соответствующих точках физической ячейки. Источники нейтронов (третий член уравнения (7)) моделируется токами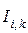 
, подводимыми в узловые точки ячеек сеточной модели в области замедлителя.
Уравнения Кирхгофа, записанные для узлов ячеек сетки, изображенных на рис. 2, имеют следующий вид:
, (9)
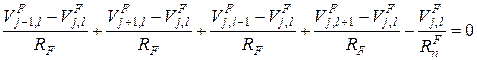. (10)
После перехода к безразмерным величинам уравнения запишутся следующим образом:
, (11)
, (12)
где 
и 
– безразмерные потенциалы; 
и 
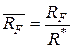–безразмерные сопротивления; 
, 
– базисные значения величин (выбираются произвольно).
Уравнения (7) и (8) и уравнения (11) и(12) имеют одинаковую форму, следовательно, распределение потенциалов в узлах сетки будет соответствовать распределению нейтронного потока в ячейке (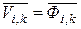
), если выполнить условие равенства коэффициентов в соответствующих членах уравнений (7) и (8) и уравнений (11) и (12). Приравнивая коэффициенты, получим условия моделирования:
; 
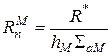; (13)
; (14)
; 
. (15)
Если Ei,k >> Vi,k, то вторым членом () в условии (14) можно пренебречь. Для этого сопротивления 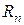нужно выбрать достаточно большими. Для упрощения модели удобно принять 
В работе моделируется квадратная ячейка уран-водного реактора со следующими характеристиками: размер ячейки (шаг решетки) – а = 3 см, диаметр ТВЭЛ – d = 1,2 см, обогащение урана – 5 %;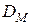 
= 0,164 см; = 0,022 см-1; 
= 0,174 см; 
= 1,49 см-1; 
= 7,45 см2; 
= 0,425 см-1; 
= 0,23 см2.
Шаг сетки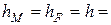 
0,15 см. Базисное значение = 1,2 ком. Величины сопротивлений в модели: 
1,1 ком,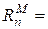 
363 ком, 
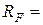230 ом, 
2,35 ком.
Схема моделируемой ячейки и расположение узловых точек показаны на рис. 3. Наличие симметрии позволяет моделировать 
часть ячейки.
Величины сопротивлений в граничных узловых точках (1-11) подсчитываются с учетом их расположения относительно границы топливо-замедлитель. На внешних границах области моделирования, т.е. при 
, 
, 
, 
выполнено граничное условие (4), что соответствует на модели отсутствию электрических токов между соответствующими узлами.
