Цель работы: решение критической задачи на модели, т.е. определение распределения нейтронных потоков в критическом реакторе и определение критического коэффициента размножения
Теоретические основы
 |
Электрические сеточные модели позволяют решать в диффузионном приближении ряд нейтронно-физических задач, в том числе задачу расчета критического состояния реактора. В настоящей работе моделируется реактор наиболее простой формы: плоский реактор с отражателем (рис.1.). При этом определяется пространственные распределения нейтронных потоков критического реактора.
Двухгрупповые диффузионные уравнения для активной зоны плоского реактора имеют следующий вид:
 ; (1)
; (1)
 , (2)
, (2)
где N и Ф – потоки быстрых и тепловых нейтронов; Dб и Dт – коэффициенты диффузии быстрых и тепловых нейтронов;  – сечение замедления;
– сечение замедления;  – сечение поглощения тепловых нейтронов;
– сечение поглощения тепловых нейтронов;  – вероятность избежать резонансного захвата;
– вероятность избежать резонансного захвата;  – коэффициент размножения для бесконечной среды.
– коэффициент размножения для бесконечной среды.
Приведенные уравнения справедливы и для отражателя, если учесть, что в отражателе k = 0 и  =1. Граничные условия (индекс «1» относится к активной зоне, «2» – к отражателю):
=1. Граничные условия (индекс «1» относится к активной зоне, «2» – к отражателю):
1) на внешней границе реактора
N = 0, Ф = 0 (3)
2) на границе активной зоны и отражателя:
N 1 = N 2
Ф 1 = Ф 2 (4)

 . (5)
. (5)
Преобразуем уравнение в конечно-разностную форму и приведем их к безразмерному виду. Шаг сетки обозначим h. Переход к конечно-разностной форме означает замену непрерывной функции распределения Ф (х) набором дискретных значении функций в узловых точках сетки. Произведем в уравнениях подстановки на основании соотношений:
 , (6)
, (6)
где  и
и  –безразмерные величины нейтронных потоков, Ф *–базисное значение потока.
–безразмерные величины нейтронных потоков, Ф *–базисное значение потока.
Кроме того, введем в уравнение базисные величины коэффициентов диффузии  и
и  (делением на них всех членов уравнения).После преобразований уравнения принимают следующий вид:
(делением на них всех членов уравнения).После преобразований уравнения принимают следующий вид:
 , (7)
, (7)
 , (8)
, (8)
где (i -1), (i +1) –номера узловых точек сетки вдоль оси х.
Электрическая сеточная модель и выбор ее параметров. Распределение нейтронных потоков, описываемое уравнениями (7) и (8) моделируются сеткой сопротивлений, два узла которой показаны на рис. 2а – активная зона и рис. 2б – отражатель

Потенциал Vi моделирует величину потока быстрых нейтронов в данной точке, Ui – величину потока тепловых нейтронов. Токи через сопротивления Rб и Rт моделируют диффузию быстрых и тепловых нейтронов, токи через сопротивление Rз моделируют замедление, а через сопротивление Rп – поглощение нейтронов. Токи Ii, которые должны подводится от внешнего источника в узлы “верхней” сетки в активной зоне, моделируют источники быстрых нейтронов, т.е процесс деления. Эти токи пропорциональны потоку тепловых нейтронов в данной точке и коэффициенту размножения, поэтому задаем функцию источника Ei = fUi
Уравнения баланса токов для узла (i, k) имеет вид:
 .
.
Перегруппируем некоторые члены уравнения и приведем уравнения к безразмерной форме Для этого выбираем базисные значения напряжений и сопротивлений U* и R* и вводим в уравнения безразмерные величины потенциалов и сопротивлений:
 ,
,  ,
,  .
.
В результате получим:
 .
. 
Уравнения (7) и (8),описывающие поведение нейтронов в реакторе, и уравнения (9) и (10), описывающие распределение потенциалов в узлах электрической модели, по форме одинаковы. Поэтому можно утверждать, что при выполнении условий моделирования распределение потенциалов в узловых точках модели подобно распределению нейтронного потока в моделируемом реакторе. Условия моделирования, т.е. формулы для расчета сопротивлений модели, можно получить, приравнивая коэффициенты в соответствующих членах уравнений (7) и(9) и уравнений (8) и (10). При этом введем масштабные коэффициенты  для потоков быстрых нейтронов:
для потоков быстрых нейтронов:
 (11)
(11)
Величина коэффициента  выбирается исходя из требований необходимой точности моделирования, причем
выбирается исходя из требований необходимой точности моделирования, причем  >>1, и чем больше величина
>>1, и чем больше величина  , тем меньше погрешность при моделировании (см. соотношения (17) и (18)).
, тем меньше погрешность при моделировании (см. соотношения (17) и (18)).
Условия моделирования для активной зоны и для отражателя (величины  ,
,  , R * выбираются произвольно):
, R * выбираются произвольно):
 ; (12)
; (12)
 ; (13)
; (13)
 ; (14)
; (14)
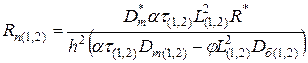 ; (15)
; (15)
 ; (16)
; (16)
 , (17)
, (17)
причем:

Обычно благодаря большой величине масштабного коэффициента  B << A, поэтому можно принять:
B << A, поэтому можно принять:
 . (18)
. (18)
Таким образом, получаем формулу, позволяющую найти коэффициент размножения в данной точке реактора, измерив потенциалы Ei и Ui на модели:
 . (19)
. (19)
Характеристики моделируемого реактора и модели. В работе моделируется распределение потоков быстрых и тепловых нейтронов в плоском реакторе с отражателем (рис.1.). Физические характеристики и размеры реактора следующие:
Толщина активной зоны – 180 см;
Толщина отражателя – 60 см;
Dб1 = Dб2 = 1,1 см; Dт1 = Dт2 = 0,9 см;
 =
=  = 300 см2;
= 300 см2;  = 250 см2;
= 250 см2;
 = 2500 см2;
= 2500 см2;  = 0,9.
= 0,9.
При расчете модели приняты следующие значения величин:
h = 20 см;  = 1 см;
= 1 см;
 = 50;
= 50;  = 0,0475 см;
= 0,0475 см;
R * = 68,4 ком.
Рассчитанные величины сопротивлений в модели:
Rп = 75,2 ком; Rз2 = 110,5 ком;
Rб1 = Rб2 = 62,2 ком; Rп1 = 2,3 ком;
Rт1 = Rт2 = 3,6 ком; Rп2 = 28,3 ком;
Rз1 = 123 ком; А = 87,94.






