


 №3 9
№3 9




 6
6

 1 4
1 4

 2 4
2 4




 6 5 2
6 5 2



 9 5
9 5
 8 7 3
8 7 3


 3 6
3 6



 2 8 3 9
2 8 3 9



 9 8
9 8
6 4
Ответ: 1-3-4-8-11-13; 15.
№4
Производственное объединение выделяет четырем входящим в него предприятиям кредит в сумме 100 млн.ден.ед. для расширения производства и увеличения выпуска продукции. По каждому предприятию известен возможный прирост  выпуска продукции (в денежном выражении) в зависимости от выделенной суммы
выпуска продукции (в денежном выражении) в зависимости от выделенной суммы  . Для упрощения вычислений выделяемые суммы кратны 20 млн ден.ед. (таблица). При этом предполагаем, что прирост выпуска продукции на i - м предприятии не зависит от суммы средств, вложенных в другие предприятия, а общий прирост выпуска в производственном объединении равен сумме приростов, полученных на каждом предприятии объединения.
. Для упрощения вычислений выделяемые суммы кратны 20 млн ден.ед. (таблица). При этом предполагаем, что прирост выпуска продукции на i - м предприятии не зависит от суммы средств, вложенных в другие предприятия, а общий прирост выпуска в производственном объединении равен сумме приростов, полученных на каждом предприятии объединения.
Выделяемые средства  , млн.ден.ед , млн.ден.ед
| Предприятие | |||
| №1 | №2 | №3 | №4 | |
Прирост выпуска продукции на предприятиях 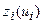 , млн. ден.ед. , млн. ден.ед.
| ||||

| 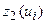
| 
| 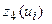
| |
Ответ: 85 (0; 20; 40; 40).
№5
Производственному объединению из трех предприятий выделяется банковский кредит в сумме 60 млн.ден.ед. для увеличения выпуска продукции. Значения  дополнительного дохода, получаемого на предприятиях объединения в зависимости от выделенной суммы
дополнительного дохода, получаемого на предприятиях объединения в зависимости от выделенной суммы  , приведены в таблице. Распределить выделенный кредит между предприятиями так, чтобы дополнительный доход объединения был максимальным.
, приведены в таблице. Распределить выделенный кредит между предприятиями так, чтобы дополнительный доход объединения был максимальным.
Выделяемые средства  , млн.ден.ед , млн.ден.ед
| Предприятие | ||
| №1 | №2 | №3 | |
Прирост выпуска продукции на предприятиях 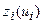 , млн. ден.ед. , млн. ден.ед.
| |||

| 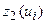
| 
| |
Ответ: 47 (0,40,20).
№6
Производственному объединению из четырех предприятий выделяется банковский кредит в сумме 60 млн.ден.ед. для увеличения выпуска продукции. Значения  дополнительного дохода, получаемого на предприятиях объединения в зависимости от выделенной суммы
дополнительного дохода, получаемого на предприятиях объединения в зависимости от выделенной суммы  , приведены в таблице. Распределить выделенный кредит между предприятиями так, чтобы дополнительный доход объединения был максимальным.
, приведены в таблице. Распределить выделенный кредит между предприятиями так, чтобы дополнительный доход объединения был максимальным.
Выделяемые средства  , млн.ден.ед , млн.ден.ед
| Предприятие | |||
| №1 | №2 | №3 | №4 | |
Прирост выпуска продукции на предприятиях 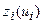 , млн. ден.ед. , млн. ден.ед.
| ||||

| 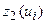
| 
| 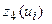
| |
Ответ: 45 (0,0,40,20).
Практическое занятие № 16
Тема «Марковские процессы»
№1 Рассмотрим состояние банка, характеризующееся одной из процентных ставок: 2%, 3%, 4%, которые устанавливаются в начале каждого квартала и фиксированы на всем его протяжении. Таким образом, если за систему S принять рассматриваемый банк, то она в каждый момент времени может находится только в одном из следующих трех состояний: 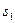 - процентная ставка 2%,
- процентная ставка 2%,  - процентная ставка 3%,
- процентная ставка 3%, 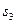 - процентная ставка 4%. Анализ работы банка в предшествующие годы показал, что изменение переходных вероятностей с течением времени пренебрежимо мало.
- процентная ставка 4%. Анализ работы банка в предшествующие годы показал, что изменение переходных вероятностей с течением времени пренебрежимо мало.
Определить вероятности указанных состояний банка в конце года, если в конце предыдущего года процентная ставка банка составляла 3%, а размеченный граф состояний банка представлен на рисунке.


|
|
|




 0,2 0,3
0,2 0,3
 0,2
0,2
0,1
№2 Предположим, что в условиях примера №1 переходные вероятности зависят от моментов установления процентных ставок. Матрицы переходных вероятностей задаются следующим образом:



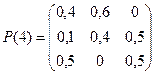 . Построить размеченные графы состояний, соответствующие моментам времени
. Построить размеченные графы состояний, соответствующие моментам времени 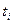 - начало i -го квартала, i =1,2,3,4 и найти вероятности состояний банка в конце года, если в конце предшествующего года процентная ставка была 4%.
- начало i -го квартала, i =1,2,3,4 и найти вероятности состояний банка в конце года, если в конце предшествующего года процентная ставка была 4%.
№3 Инвестиционный фонд размещает средства предприятий в наиболее ликвидные на рынке активы по одной из следующих годовых процентных ставок: 25%, 30%, 35%, которые устанавливаются фондом в начале каждого из рассматриваемых трех месяцев и остаются неизменными на всем его протяжении. Матрицы переходных вероятностей задаются следующим образом: 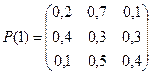
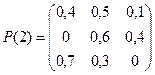
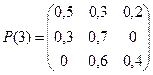 . Построить размеченные графы состояний инвестиционного фонда, соответствующие рассматриваемым месяцам. Определить вероятности данных процентных ставок на третьем месяце, если в месяце, предшествующем первому из рассматриваемых месяцев, инвестиционный фонд мог разместить средства предприятий под 30% годовых.
. Построить размеченные графы состояний инвестиционного фонда, соответствующие рассматриваемым месяцам. Определить вероятности данных процентных ставок на третьем месяце, если в месяце, предшествующем первому из рассматриваемых месяцев, инвестиционный фонд мог разместить средства предприятий под 30% годовых.
№4 Рассмотрим состояние банка  ,
,  ,
, 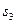 ,
,  характеризующееся соответственно процентными ставками 3%, 5%, 7%, 10%, которые устанавливаются в начале каждого месяца и фиксированы на всем его протяжении. Наблюдение за работой банка в предшествующий период показало, что переходные вероятности состояний в течение квартала остаются неизменными.
характеризующееся соответственно процентными ставками 3%, 5%, 7%, 10%, которые устанавливаются в начале каждого месяца и фиксированы на всем его протяжении. Наблюдение за работой банка в предшествующий период показало, что переходные вероятности состояний в течение квартала остаются неизменными.
Определить вероятности состояний банка в конце квартала, если в конце предшествующего квартала процентная ставка составляла 55, а размеченный граф состояний банка имеет следующий вид:
 |

 0,6
0,6
0,2 0,1

|
|



 0,4
0,4
|
0,3 0,4
№5 Допустим, что в условиях задачи №4 переходные вероятности зависят от моментов установления процентных ставок. Матрицы переходных вероятностей задаются следующим образом:
 ,
,  ,
, 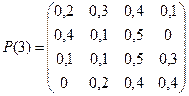 .
.
Постройте размеченные графы состояний, соответствующие началам каждого месяца в квартале, и найдите вероятности состояний банка в конце квартала, если в конце предшествующего квартала процентная ставка составляла 3%.
Практическое занятие №17
В приведенных ниже примерах СМО выделите их основные элементы: входящий поток заявок, каналы обслуживания, выходящий поток заявок.
№1. На таможенном посту работают три инспектора, занимающиеся досмотром транспорта, пересекающего границу. Машины, подъезжающие к посту, становятся в очередь и ожидают досмотра.
№2. В одном из отделений сбербанка работают два кассира, принимающие коммунальные платежи. Каждый кассир одновременно может обслужить только одного клиента. Если клиент заходит в отделение, когда кассиры заняты обслуживанием, он может не ожидать обслуживания и зайти в другое отделение.
№3. На одну телефонную линию поступает простейший поток вызовов с интенсивностью λ=0,9 вызовов в минуту. Производительность телефонной линии μ=0,7 вызовов в минуту (поток обслуживаний - простейший). Вызов, поступивший в момент занятости телефонной линии, получает отказ. Определить предельные значения относительной пропускной способности Q, абсолютной пропускной способности А и вероятности отказа  , среднее время обслуживания одного вызова, вероятность того, что канал свободен, вероятность того, что канал занят.
, среднее время обслуживания одного вызова, вероятность того, что канал свободен, вероятность того, что канал занят.
№4 Телефонная АТС имеет одну линию, на которую в среднем приходит 0,8 вызова в минуту. Средне время разговора 1,5 мин. Вызов, пришедший во время разговора, не обслуживается. Считая потоки вызовов пуассоновскими, найти абсолютную и относительную пропускную способности станции и вероятность отказа абоненту.
№5 На вокзале, в мастерской бытового обслуживания работают 3 мастера. Если клиент заходит в мастерскую, когда все мастера заняты, то он уходит из мастерской не ожидая обслуживания. Среднее число клиентов, обращающихся в мастерскую за 1 час, равно 20. Среднее время, которое затрачивает мастер на обслуживание одного клиента, равно 6 мин. Определить основные характеристики эффективности функционирования данной мастерской в предельном режиме:
1) вероятность того, что клиент получит отказ;
2) вероятность того, что клиент будет обслужен;
3) среднее число клиентов, обслуживаемых мастерской в течение 1 часа;
4) среднее число занятых мастеров.
№6 В отделении банка на обслуживании клиентов работают 3 оператора. Среднее время обслуживания одного клиента оператором 12 минут. В среднем за час в банк обращается 15 клиентов. Если все операторы заняты, клиенты не обслуживаются банком. Найти основные средние характеристики работы банка, а также вероятность того, что не менее двух каналов простаивают.
№7 Один наладчик обслуживает 6 автоматов. Интенсивность поломок каждого автомата λ=1 (поломка в час). Среднее время, которое тратит наладчик на ремонт одного автомата равно 0,1 ч. Определить предельные вероятности состояний данной СМО и найти среднее число неисправных автоматов, т.е. находящихся в ремонте и ожидающих ремонта. Также определить:
1) вероятность того, что наладчик занят ремонтом автоматов;
2) абсолютную пропускную способность СМО;
3) относительную пропускную способность СМО;
4) среднее число неисправных автоматов;
5) среднее число автоматов, ожидающих в очереди ремонта;
6) среднее число автоматов в ремонте.
№8 Бригада из трех человек обслуживает 20 автоматов. Интенсивность поломки каждого автомата λ=1 (поломка в час). Среднее время, которое тратит один наладчик на ремонт одного автомата, равно 0,1 ч. Определить предельные вероятности состояний данной СМО и найти среднее число неисправных автоматов (т.е. находящихся в ремонте и ожидающих ремонта), среднее число автоматов в очереди, ожидающих ремонта, среднее число свободных наладчиков. Также определить:
1) среднее число занятых каналов (среднее число автоматов под обслуживанием);
2) абсолютную пропускную способность СМО;
3) относительную пропускную способность СМО;
4) среднее число автоматов в системе (под обслуживанием и в очереди);
5) среднее число автоматов в очереди.






