Привести к стандартной форме ЗЛП.
№12
Привести к стандартной форме ЗЛП. Найти общее и базисное решения системы ограничений.
№13
Практическое занятие №2
Тема «Графический метод решения задачи линейного программирования»
Решить ЗЛП графическим методом.
№1 №2
Ответ: 
при х 1=6, х 2=2 Ответ: 
=6, точки отрезка с концами (1; 
), (5; 
).
№3 №4
Ответ: решений нет. Ответ: 
при х 1=1, х 2=5
№5 №6
Ответ: 
Ответ: =18 при х 1=0, х 2=6
№7
Ответ: 
при х 1= х 2= 
; =6, точки отрезка с концами (4;2), (1;5).
№8 №9
Ответ: =13 при х 1=5, х 2=3 Ответ: =24 при х 1=6, х 2=4
Практическое занятие №3
Тема «Симплексный метод решения задач линейного программирования (симплексные таблицы)»
Решить ЗЛП симплексным методом (симплексные таблицы).
№1 №2
Ответ: 
Ответ: 
№3 №4
Ответ: 
(
) Ответ: 
№5 №6
Ответ: 
Ответ: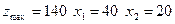 
Практическое занятие №4
Тема «Метод искусственного базиса»
Решить с помощью М -метода
№1 №2
Ответ: 
Ответ: 
№3 №4
Ответ: 
Ответ: задача не имеет решения.
№5 №6
Ответ: 
Ответ: 
№7 №8
Ответ: задача не имеет решения. Ответ: задача не имеет решения.
Практическое занятие №5
Тема «Двойственные задачи линейного программирования»
Построить двойственные задачи к ЗЛП в симметричной форме
№1 №2 №3 №4
№5
Пусть имеются ЗЛП в произвольной форме, построить им двойственные задачи
№6 №7
Для данных задач составить двойственные и применив первую и вторую терему двойственности найти решение двойственных задач (исходные задачи решены при выполнении практического занятия №3).
№8 (практическое занятие №1, задача №2)
.
№9 (практическое занятие №1 задача №1)
№10 (практическое занятие №3, задача №3)
.
№11 (практическое занятие №3, задача №2)
.
Практическое занятие №6
Тема «Целочисленные задачи линейного программирования.
Метод Гомори»
Графическим методом и методом ветвей и границ решить задачу целочисленного программирования
№1
Ответ: =11 при х 1=1, х 2=5.
№2
,
Ответ: =29 при х 1=2, х 2=5.
Решить методом Гомори.
№3
Ответ: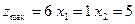 
№4
Ответ: 
№5
Ответ: 
№6
Ответ: 
№7
Ответ: 
№8
Ответ: 
№9
Ответ: 
Практическое занятие №7
Тема «Транспортная задача»
В пунктах А1, А2, А3 производится однородная продукция в количествах а1, а2, а3 единиц. Готовая продукция поставляется в пункты В1, В2, В3, В4, потребности которых составляют b1, b2, b3, b4 единиц. Стоимости сij перевозок единицы продукции из пункта Аi в пункт Вj заданы матрицей 
. Требуется
Составить методом минимального элемента опорный план задачи;
Методом потенциалов найти план перевозок продукции, при котором минимизируются суммарные затраты по ее доставке потребителям;
Вычислить суммарные затраты.
№1 а1= 500 а2= 200 а3= 600 b1= 250 b2= 150 b3= 350 b4= 250
№2 а1= 500 а2= 900 а3= 100 b1= 200 b2= 650 b3= 150 b4= 300
№3 а1= 450 а2= 200 а3= 350 b1= 150 b2= 300 b3= 50 b4= 400
№4 а1= 750 а2= 200 а3= 550 b1= 450 b2= 300 b3= 350 b4= 250
Практическое занятие №8
Тема «Нелинейное программирование.
Решение задач нелинейного программирования
методом множителей Лагранжа»
Найти условные экстремумы функций методом Лагранжа
№1 
при условии 
Ответ: 
=2,77 в точке (
) или (1,38; 0,92).
№2 
при условии 
, 
Ответ: =17278 в точке (91;89).
№3 
при условии 
Ответ: =0,6 в точке (0,83; 0,55), 
=-0,6 в точке (-0,83; -0,55).
№4 
при условии 
,
№5 при условии 
№6 
при условии 
№7 
при условии 
Ответ: =9 в точке (1;-2;2), =-9 в точке (-1;2;-2).
Практическое занятие №9
Тема «Нелинейное программирование.
