В 80-х годах в США был принят стандарт симметричного криптоалгоритма для внутреннего применения DES, который получил достаточно широкое распространение в свое время. Однако на текущий момент этот стандарт полностью неприемлем для использования по двум причинам:
1) основной – длина его ключа составляет 56 бит, что чрезвычайно мало на современном этапе развития ЭВМ;
2) второстепенной – при разработке алгоритм был ориентирован на аппаратную реализацию, то есть содержал операции, выполняемые на микропроцессорах за неприемлемо большое время (например, такие как перестановка бит внутри машинного слова по определенной схеме).
Все это привело к тому, что в 1997 году Американский институт стандартизации (NIST) объявил конкурс на новый стандарт симметричного криптоалгоритма (AES – Advanced Encryption Standard).
На первом этапе в оргкомитет соревнования поступило 15 заявок из разных стран мира. В течение 2 лет специалисты комитета, исследуя самостоятельно, и изучая публикации других исследователей, выбрали 5 лучших представителей, прошедших в финал соревнования: MARS, RC3, Rijndael, Serpent и TwoFish. Все эти алгоритмы были признаны достаточно стойкими и успешно противостоящими всем широко известным методам криптоанализа.
2 октября 2000 года NIST объявил о своем выборе: победителем конкурса стал бельгийский алгоритм Rijndael, разработанный Йоаном Даменом (Joan Daemen) и Винсентом Райменом (Vincent Rijnmen). Название алгоритма составлено из первых букв фамилий авторов.
Шифр Rijndael выполнен в архитектуре "Квадрат" (Square) и имеет следующие параметры:
· размер блока – 128, 192 или 256 бит;
· размер ключа – 128, 192 или 256 бит;
· число раундов – 10, 12 или 14.
В алгоритме Rijndael блоки открытых и зашифрованных данных, соответственно T и T', представляются в виде массивов из N = 16, 24 или 32 байтов. В ходе криптографических преобразований исходный и зашифрованный блоки данных, а также все промежуточные результаты процесса шифрования (состояния) интерпретируются как матрицы байтов, содержащие по 4 строки. Таким образом, в зависимости от размера блока, размер матрицы составляет  байта. Количество столбцов
байта. Количество столбцов  , где
, где  . Матрицы заполняются байтами входного блока (открытого текста при шифровании и шифртекста при расшифровании) по столбцам – сверху вниз и слева направо, и
. Матрицы заполняются байтами входного блока (открытого текста при шифровании и шифртекста при расшифровании) по столбцам – сверху вниз и слева направо, и
точно в таком же порядке извлекаются байты из матрицы-результата:

 . (3.3)
. (3.3)
Схема преобразования данных при шифровании показана на рис. 3.3. На рисунке использованы следующие обозначения: T, T ' – открытый и зашифрованный блоки данных соответственно;  – i -тый ключевой элемент; F, F ' – регулярное нелинейное преобразование и преобразование последнего раунда соответственно;
– i -тый ключевой элемент; F, F ' – регулярное нелинейное преобразование и преобразование последнего раунда соответственно;  – промежуточное состояние шифруемого блока после прибавления i -того ключевого элемента; R – количество раундов шифрования.
– промежуточное состояние шифруемого блока после прибавления i -того ключевого элемента; R – количество раундов шифрования.

|
| Рис. 3.3. Схема преобразования информации в алгоритме шифрования блока Rijndael. |
Как видно на рис. 3.3, процесс шифрования состоит из чередующихся прибавлений ключевых элементов к блоку данных и нелинейного преобразования этого блока:
 .
.
Число раундов шифрования определяется в зависимости от размера блока и ключа: из двух размеров выбирается максимальный, и если он равен 128 бит, то используется 10 раундов, если 192 бита, то 12, и если 256 – то 14 раундов. Эту зависимость можно представить таблицей 3.2.
Таблица 3.2
Зависимость количества раундов от размеров блока и ключа
в алгоритме Rijndael
| Размер блока (бит) | Размер ключа (бит) | ||
Прибавление ключевых элементов, которым начинается и заканчивается процесс шифрования, а также некоторые другие операции раундового преобразования выполняется побайтно в конечном поле Галуа GF(28). Операцией сложения в нем является побитовое сложение по модулю 2. Соответственно, каждый ключевой элемент является байтовой матрицей того же самого размера, что и блок данных.
За один раунд шифрования преобразуется полный блок данных, а не его часть, как в сетях Фейстеля. На последнем раунде функция нелинейного преобразования отличается от аналогичной функции, используемой в остальных раундах – это сделано для обеспечения алгоритмической эквивалентности прямого и обратного преобразований шифрования.
Нелинейное преобразование F матрицы данных состоит из трех шагов: ByteSub – замены байтов матрицы на новые значения (S[]), ShiftRows – циклического сдвига строк матрицы влево ( ) и MixColumns – умножения матрицы данных слева на постоянную матрицу-циркулянт M:
) и MixColumns – умножения матрицы данных слева на постоянную матрицу-циркулянт M:
 .
.
Все входные (X), выходные (X') и промежуточные значения преобразования являются матрицами байтов одинакового размера  .
.
Функция преобразования последнего раунда F' отличается от регулярной функции преобразования F отсутствием шага MixColumns:
 .
.
В преобразовании ByteSub каждый байт исходной матрицы данных заменяется новым значением в соответствии с единственной таблицей замены (S-Box). В этой таблице замен (табл. 3.3) заменяющее значение выбирается на пересечении строки, определяемой старшей 16-ричной цифрой заменяемого значения, и столбца, определяемого его младшей цифрой.
Таблица 3.3
Таблица замен преобразования ByteSub
| x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | xA | xB | xC | xD | xE | xF | |
| 0x | 7c | 7b | f2 | 6b | 6f | c5 | 2b | fe | d7 | ab | ||||||
| 1x | ca | c9 | 7d | fa | f0 | ad | d4 | a2 | af | 9c | a4 | c0 | ||||
| 2x | b7 | fd | 3f | f7 | cc | A5 | e5 | f1 | d8 | |||||||
| 3x | c7 | c3 | 9a | e2 | eb | b2 | ||||||||||
| 4x | 2c | 1a | 1b | 6e | 5a | a0 | 3b | d6 | b3 | e3 | 2f | |||||
| 5x | d1 | ed | fc | b1 | 5b | 6a | cb | be | 4a | 4c | cf | |||||
| 6x | d0 | ef | aa | fb | 4d | f9 | 7f | 3c | 9f | a8 | ||||||
| 7x | a3 | 8f | 9d | f5 | bc | b6 | da | ff | f3 | d2 | ||||||
| 8x | cd | 0c | ec | 5f | c4 | a7 | 7e | 3d | 5d | |||||||
| 9x | 4f | dc | 2a | ee | b8 | de | 5e | 0b | db | |||||||
| Ax | e0 | 3a | 0a | 5c | c2 | d3 | ac | e4 | ||||||||
| Bx | e7 | c8 | 6d | 8d | d5 | 4e | a9 | 6c | f4 | ea | 7a | ae | ||||
| Cx | ba | 2e | 1c | a6 | b4 | c6 | e8 | dd | 1f | 4b | bd | 8b | 8a | |||
| Dx | 3e | b5 | f6 | 0e | b9 | c1 | 1d | 9e | ||||||||
| Ex | e1 | f8 | d9 | 8e | 9b | 1e | e9 | ce | df | |||||||
| Fx | 8c | a1 | 0d | bf | e6 | 2d | 0f | b0 | bb |
В ходе операции ShiftRows каждая строка матрицы данных, кроме первой, циклически сдвигается влево на определенное число позиций, зависящее от номера строки и от числа столбцов матрицы. Табл. 3.4 описывает указанную зависимость.
Таблица 3.4
Зависимость количества сдвигов строки
в преобразовании ShiftRows
| № строки | Количество столбцов (n) | ||
На шаге MixColumns каждый столбец исходной матрицы слева умножается на постоянную матрицу-циркулянт M:
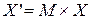 ,
,
 .
.
При выполнении матричного умножения операции сложения и умножения выполняются в конечном поле GF(28). Матрица M является циркулянтом: каждая ее строка получается циклическим сдвигом предыдущей строки вправо на один элемент. Элементы матрицы выбраны таким образом, чтобы свести к минимуму трудоемкость операции умножения: в ней присутствуют лишь небольшие по значению числа 01, 02 и 03, половина элементов – единичные, т.е. реального умножения выполнять для них не требуется. Этим самым обеспечивается высокая эффективность возможных реализаций этой операции.
Следует добавить, что операция умножения в конечном поле GF(28) является достаточно трудоемкой в программной реализации и никаким образом не сводится к обычному арифметическому умножению. Если умножение двоичных чисел реализуется сдвигами и обычным арифметическим суммированием, то умножение полиномов над полем GF(28) – теми же сдвигами и побитовым суммированием по модулю 2. Однако в шифре Rijndael одним из множителей всегда является константа и размер операндов невелик – один байт. Это позволяет реализовать умножение на константу в поле GF(28) как замену, что существенно повышает эффективность программной реализации. Для каждого множителя-константы при этом требуется свой отдельный узел замен. Напротив, наиболее эффективной аппаратной реализацией этой операции является реализация в виде серии сдвигов и побитовых сложений по модулю два в соответствие с ее непосредственным определением.
Рис. 3.4 иллюстрирует операции ByteSub, ShiftRows и MixColumns.
Размер ключа в шифре Rijndael равен 128, 192 или 256 бит. Размер ключевого элемента, используемого на раунде, совпадает с размером блока и также равен 128, 192 или 256 бит независимо от размера ключа. Число раундов шифрования находится в пределах от 10 до 14. Массив ключевых элементов вырабатывается из ключа шифрования с использованием KeyExpansion – процедуры "развертывания" ключа.
Алгоритм KeyExpansion (развертывания ключа) оперирует 32-битовыми ключевыми словами Wi, интерпретируя их как четырехбайтовые массивы:  .
.
Первые  (здесь
(здесь  – количество байтов ключа) ключевых слов получаются простым разделением ключа K на 4-байтовые фрагменты аналогично тому, как байтами шифруемого блока заполняются столбцы матрицы данных:
– количество байтов ключа) ключевых слов получаются простым разделением ключа K на 4-байтовые фрагменты аналогично тому, как байтами шифруемого блока заполняются столбцы матрицы данных:

Необходимое число ключевых элементов на 1 больше числа раундов R, каждый ключевой элемент по размеру равен блоку данных ( байт) и содержит
байт) и содержит  ключевых слов. Таким образом, всего необходимо
ключевых слов. Таким образом, всего необходимо  ключевых слов.
ключевых слов.

|
| Рис. 3.4. Иллюстрация основных операций шифра Rijndael. |
Первые q ключевых слов составлены из байтов ключа как показано выше, остальные Q – q вырабатываются по следующему алгоритму.
При размере ключа 16 или 24 байта ( ) используется следующая итерационная формула:
) используется следующая итерационная формула:

а при размере ключа 32 байта (q = 8) – следующая:

В приведенных выше формулах использованы следующие обозначения: S(W) – побайтовая замена с использованием штатного узла замен S,  – циклический сдвиг 4-байтового вектора на один элемент влево,
– циклический сдвиг 4-байтового вектора на один элемент влево,  – раундовая константа, представляющая собой 4-байтовый вектор
– раундовая константа, представляющая собой 4-байтовый вектор  , где возведение в степень выполняется в поле GF(28).
, где возведение в степень выполняется в поле GF(28).
Таким образом, все усложняющее преобразование может быть представлено в следующей форме:

Как видно из приведенных выше соотношений, ключевые слова вырабатываются порциями, по размеру равными ключу, причем первое слово каждой порции вырабатывается по усложненной схеме с использованием приведенного выше нелинейного преобразования, а остальные – простым побитовым суммированием непосредственно предшествующего элемента с элементом, имеющим тот же порядковый номер в предыдущей порции ключевых слов. При размере ключа 256 бит (32 байта) усложнение используется также и при выработке каждого пятого элемента порции – при нумерации с нуля он имеет индекс 4 в группе из q слов.
Каждые последовательно выработанные  ключевых слов (включая и те, что получены непосредственно из ключа) объединяются в раундовые ключевые элементы:
ключевых слов (включая и те, что получены непосредственно из ключа) объединяются в раундовые ключевые элементы:
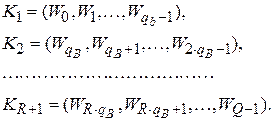
Ключевые элементы, как и блок данных, к которому они прибавляются в процессе шифрования, может быть представлен в виде матрицы байтов размера  .
.
В этом случае столбцы матрицы ключевого элемента образуются ключевыми словами:

Процесс расшифрования блока данных алгоритмически идентичен процессу его шифрования (рис. 3.3), если через T обозначить блок зашифрованных данных, а через T' – открытых. Расшифрование отличается от шифрования по следующим четырем пунктам:
1. Ключевые элементы используются в порядке, обратном тому, в котором они используются при шифровании. Кроме того, все ключевые элементы, кроме первого и последнего, должны быть умножены слева на матрицу, обратную матрице M. Таким образом, если при шифровании используется следующая последовательность ключевых элементов  , то при расшифровании должна быть использована следующая последовательность элементов:
, то при расшифровании должна быть использована следующая последовательность элементов:  .
.
2. На шаге побайтовой замены используется узел замен  обратный тому, что применяется в процедуре шифрования S. Это означает, что каково бы ни было байтовое значение b, всегда справедливо следующее соотношение:
обратный тому, что применяется в процедуре шифрования S. Это означает, что каково бы ни было байтовое значение b, всегда справедливо следующее соотношение:  . Указанный узел замен
. Указанный узел замен  представлен в табл. 3.5.
представлен в табл. 3.5.
Таблица 3.5
Таблица замен обратного преобразования ByteSub
| x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | xA | xB | xC | xD | xE | xF | |
| 0x | 6a | d5 | a5 | bf | a3 | 9e | f3 | d7 | fb | |||||||
| 1x | 7c | e3 | 9b | 2f | ff | 8e | c4 | de | e9 | cb | ||||||
| 2x | 7b | a6 | c2 | 3d | ee | 4c | 0b | fa | c3 | 4e | ||||||
| 3x | 2e | a1 | d9 | b2 | 5b | a2 | 6d | 8b | d1 | |||||||
| 4x | f8 | f6 | d4 | a4 | 5c | cc | 5d | b6 | ||||||||
| 5x | 6c | fd | ed | b9 | da | 5e | a7 | 8d | 9d | |||||||
| 6x | d8 | ab | 8c | bc | d3 | 0a | f7 | e4 | b8 | b3 | ||||||
| 7x | d0 | 2c | 1e | 8f | ca | 3f | 0f | c1 | af | bd | 8a | 6b | ||||
| 8x | 3a | 4f | dc | ea | f2 | cf | ce | f0 | b4 | e6 | ||||||
| 9x | ac | e7 | ad | e2 | f9 | e8 | 1c | df | 6e | |||||||
| Ax | f1 | 1a | 1d | c5 | 6f | b7 | 0e | aa | be | 1b | ||||||
| Bx | fc | 3e | 4b | c6 | d2 | 9a | db | c0 | fe | cd | 5a | f4 | ||||
| Cx | 1f | dd | a8 | c7 | b1 | ec | 5f | |||||||||
| Dx | 7f | a9 | b5 | 4a | 0d | 2d | e5 | 7a | 9f | c9 | 9c | ef | ||||
| Ex | a0 | e0 | 3b | 4d | ae | 2a | f5 | b0 | c8 | eb | bb | 3c | ||||
| Fx | 2b | 7e | ba | d6 | e1 | 0c | 7d |
3. На шаге построчного вращения матрицы данных осуществляется циклический сдвиг строк на то же самое количество элементов, что и при шифровании, но в обратную сторону – вправо.
4. На шаге умножения слева на постоянную матрицу используется матрица  , обратная используемой при шифровании матрице M:
, обратная используемой при шифровании матрице M:







