В 1960 г. было произведено 1283 тыс. т кокса. В 1913 г. – 285 тыс. т стали. В 1940 г. – 124 тыс. т чугуна. В 1950 г. – 772 тыс. т проката. В 1994 г. – 494 тыс.т чугуна. В I960 г. – 1482 тыс. т стали. В 1940 г. – 386 тыс. т проката. В 1992 г. – 642 тыс. т кокса. В 1950 г. – 1027 тыс. т стали. В 1980 г. – 523 тыс. т кокса. В 1940 г. – 428 тыс. т стали. В 1960 г. – 1259 тыс. т проката. В 1970 г. – 716 тыс. т чугуна. В 1940 г. – т кокса. В 1950 г. – 360 тыс. т чугуна. В 1913 г. – 203 тыс. т проката. В 1980 г. – 1771 тыс. т стали. В 1994 г. – 363 тыс. т кокса. В I960 г. – 502 тыс. т чугуна. В 1970 г. – 1658 тыс. т стали. В 1913 г. – 155 тыс. т чугуна. В 1980 г. – 1442 тыс. т проката. В 1992 г. – 664 тыс. т чугуна. В 1970 г. – 1161 тыс. т кокса. В 1992 г. – 1371 тыс. т проката. В 1994 г. – 615 тыс. т стали. В 1980 г. – 913 тыс. т чугуна. В 1970 г. – 1358 тыс. т проката. В 1992 г. – 1037 тыс. т стали.
1.4. Построить поверхность:
. Отрезки х, у и шаг определить самостоятельно.
1.5. Построить поверхность 2-го порядка:
гиперболический параболоид: 
. Отрезки х, у и шаг определить самостоятельно.
Примечание. Здесь а, b, с – некоторые переменные. При необходимости можно воспользоваться любым справочником по высшей математике.
2. Решить задачу, используя функцию ЕСЛИ.
В сельскохозяйственном кооперативе работают 10 сезонных рабочих. Собирают помидоры. Оплата труда производится по количеству собранных овощей. Дневная норма сбора составляет k килограммов. Сбор 1 кг помидоров стоит m рублей. Сбор каждого килограмма сверх нормы оплачивается в 2 раза дороже. Сколько денег в день получит каждый рабочий за собранный урожай?
3. Обобщение данных (см. Приложение)
4. Линейная оптимизационная задача.
Трикотажная фабрика использует для производства свитеров и кофт три вида пряжи: А, В и С,
запасы которых составляют соответственно 900, 400 и 300 кг. Количество пряжи каждого вида (в кг), необходимой для изготовления 10 изделий, а также прибыль, получаемая от их реализации, приведены в таблице:
| Вид сырья | Затраты пряжи на 10 шт. | |
| свитера | кофточки | |
| А | ||
| В | ||
| С | ||
| Прибыль ($) | 5 |
Установить план выпуска изделий, максимизирующий прибыль.
Вариант 7
1. 1. Построить в одной системе координат при х Î [0; 2] графики следующих функций:
у1=Sin(3px)+2Sin(2px)Cos(3px)
y2=Cos(px)- Cos(3px)Sin2(px)
Шаг определить самостоятельно.
1.2. Построить в разных системах координат при х Î [-2; 2] графики следующих функций:
а) с одним условием б) с двумя условиями
1.3. На основе данных составить таблицу и построить не менее 3 - 4 произвольных графиков и диаграмм:
Важнейшие проливы
Длина пролива Босфор - 30 км. Наименьшая ширина Магелланова пролива - 2200 м. Наименьшая глубина судоходной части Ормузского пролива - 27 м. Гудзонов пролив находится в Северном Ледовитом океане. Наименьшая ширина Гибралтарского пролива - 14 км. Пролив Ла-Манш находится в Атлантическом океане. Наименьшая глубина судоходной части Баб-эль-Мандебского пролива - 31 м. Длина Ормузского пролива - 195 км. Пролив Дарданеллы находится в Атлантическом океане. Длина Гудзонова пролива - 806 км. Наименьшая глубина судоходной части Магелланова пролива - 29 м. Длина Берингова пролива - 96 км. Наименьшая ширина пролива Босфор - 700 м. Наименьшая глубина судоходной части пролива Дарданеллы - 29 м. Длина пролива Ла-Манш - 578 км. Баб-эль-Мандебский пролив находится в Индийском океане. Наименьшая глубина судоходной части Берингова пролива - 36 м. Длина Магелланова пролива - 575 км. Гибралтарский пролив находится в Атлантическом океане. Длина пролива Дарданеллы - 120 км. Наименьшая ширина Гудзонова пролива - 115 км. Наименьшая глубина судоходной части Гибралтарского пролива - 53 м. Наименьшая ширина Ормузского пролива - 54 км. Наименьшая глубина судоходной части пролива Ла-Манш - 23 м. Пролив Босфор находится в Атлантическом океане. Наименьшая ширина пролива Дарданеллы - 1300 м. Длина Баб-эль-Мандебского пролива - 109 км. Наименьшая глубина судоходной части Гудзонова пролива - 141 м. Берингов пролив находится в Тихом океане. Наименьшая ширина Баб-эль-Мандебского пролива - 26 км. Магелланов пролив находится в Тихом океане. Наименьшая ширина пролива Ла-Манш - 32 км. Наименьшая глубина судоходной части пролива Босфор - 20 м. Длина Гибралтарского пролива - 59 км. Ормузский пролив находится в Индийском океане. Наименьшая ширина Берингова пролива - 86 км.
1.4. Построить поверхность:
. Отрезки х, у и шаг определить самостоятельно.
1.5. Построить поверхность 2-го порядка:
эллипсоид: 
. Отрезки х, у и шаг определить самостоятельно.
Примечание. Здесь а, b, с – некоторые переменные. При необходимости можно воспользоваться любым справочником по высшей математике.
2. Решить задачу, используя функцию ЕСЛИ.
Если количество баллов, полученных при тестировании, не превышает 12, то это соответствует оценке «2»; оценке «З» соответствует количество баллов от 12 до 15; оценке «4» - от 16 до 20; оценке «5» - свыше 20 баллов. Составить ведомость, тестирования, содержащую сведения: фамилия, количество баллов, оценка.
3. Обобщение данных (см. Приложение)
4. Линейная оптимизационная задача.
Фирма выпускает два типа строительных материалов: А и В. Продукция обоих видов поступает в продажу. Для производства материалов используется два исходных продукта: I и II. Максимально возможные суточные запасы этих продуктов составляют 7 и 9 тонн соответственно. Расходы продуктов I и II на 1 тонну материалов приведены в таблице. Суточный спрос на материал В не превышает спроса на материал А более чем на 1 тонну. Кроме того, спрос на материал А не превышает 3 т в сутки. Оптовые цены одной тонны материалов равны: 3000 у.е для А и 4000 у.е для В. Какое количество материала каждого вида должна производить фабрика, чтобы доход от реализации был максимальным?
| Исходный продукт | Расход исходных продуктов, т (на 1 т. материалов) | Максимально возможный запас, т | |
| Материал А | Материал В | ||
| I | |||
| II |
Вариант 8
1. 1. Построить в одной системе координат при х Î [0; 3] графики следующих функций:
у1=2Sin(2px)Cos(2px)
y2=Cos2(3px)Sin2(3px)
Шаг определить самостоятельно.
1.2. Построить в разных системах координат при х Î [-2; 2] графики следующих функций:
а) с одним условием б) с двумя условиями
1.3. На основе данных составить таблицу и построить не менее 3 - 4 произвольных графиков и диаграмм:
Крупнейшие реки
Обь находится в Азии. Средний расход воды в Амуре - 10900 куб. м./с. Миссисипи находится в Северной Америке. Площадь бассейна Янцзы - 1809 тыс. кв. км. Длина Нила (с Кагерой) - 6671 км. Средний расход воды в Миссисипи -19000 куб.м./с. Площадь бассейна Амазонки (от истока р. Мараньон) - 6915 тыс. кв. км. Меконг находится в Азии. Площадь бассейна Хуанхэ - 771 тыс. кв. км. Средний расход воды в Оби - 12700 куб. м./с. Длина Янцзы - 5800 км. Нил находится в Африке. Площадь бассейна Миссисипи (с Миссури) - 3268 тыс. кв. км. Средний расход воды в Амазонке - 220000 куб. м./с. Длина Хуанхэ - 4845 км. Амазонка находится в Южной Америке. Площадь бассейна Амура (с Аргунью) - 1855 тыс. кв. км. Средний расход воды в Янцзы - 34000 куб. м./с. Длина Меконга - 4500 км. Хуанхэ находится в Азии. Средний расход воды в Ниле - 2600 куб. м./с. Длина Миссисипи (с Миссури) - 6420 км. Амур находится в Азии. Длина Оби (с Иртышом) - 5410 км. Средний расход воды в Меконге - 13200 куб. м./с. Площадь бассейна Нила (с Кагерой) - 2870 тыс. кв. км. Янцзы находится в Азии. Длина Амура (с Аргунью) - 4440 км. Средний расход воды в Хуанхэ - 2000 куб. м./с. Площадь бассейна Меконга - 810 тыс. кв. км. Длина Амазонки (от истока р. Мараньон) - 6400 км. Площадь бассейна Оби (с Иртышом) - 2990 тыс. кв. км.
1.4. Построить поверхность:
. Отрезки х, у и шаг определить самостоятельно.
1.5. Построить поверхность 2-го порядка:
однополосный гиперболоид: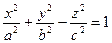 
. Отрезки х, у и шаг определить самостоятельно.
Примечание. Здесь а, b, с – некоторые переменные. При необходимости можно воспользоваться любым справочником по высшей математике.
2. Решить задачу, используя функцию ЕСЛИ.
Компания по снабжению электроэнергией взимает плату с клиентов по тарифу: k рублей за 1 Квт/ч за первые 50 кВт/ч и m рублей за каждый кВт/ч сверх нормы, которая составляет 50 кВт/ч. Услугами компании пользуются 10 клиентов. Подсчитать плату для каждого клиента.
3. Обобщение данных (см. Приложение)
4. Линейная оптимизационная задача.
Компания извлекает из руды минералы А и В. Количество минералов А и В, извлекаемых из руды типа 1 и типа 2, указаны в таблице:
| Руда типа 1 | Руда типа 2 | |
| Минерал А (кг) | ||
| Минерал В (кг) |
Тонна руды типа 1 стоит $50, тонна руды типа 2 - $60. Компания должна произвести не менее 3т минерала А и 2,5т минерала В. Сколько тонн руды каждого типа нужно закупить с минимальными затратами на покупку?
Вариант 9
1.1. Построить в одной системе координат при х Î [-2; 2] графики следующих функций:
у1= 3Sin(2px)Cos(px)Sin(px)- Cos2(3px)
y2=2Cos2(2px)-3Sin(3px)
Шаг определить самостоятельно.
1.2. Построить в разных системах координат при х Î [-2; 2] графики следующих функций:
а) с одним условием б) с двумя условиями
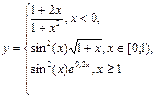
1.3. На основе данных составить таблицу и построить не менее 3 - 4 произвольных графиков и диаграмм:
