Наиболее общей формой закона распределения является функция распределения, представляющая собой вероятность того, что случайная величина Х примет значение меньшее, чем заданное х.
F(х)=Р{X<x} (2).
ФункциюF(x) иногда называют интегральной функцией распределения или интегральным законом распределения.
Геометрически функция распределения интерпретируется как вероятность того, что случайная точка Х попадет левее заданной точки х.
Дан ряд распределения случайной величины Х.
| xi | ||||
| pi | 0,4 | 0,3 | 0,1 | * |
Найти значение *, найти и изобразить графически функцию распределения.
Решение: так как сумма всех вероятностей, стоящих в нижней строке есть величина равная 1, *=1-(0,4+0,3+0,1)=0,2. Т.е. вероятность того, что случайная величина Х примет значение 7, равна 0,2.
Для нахождения функции распределения б удем задавать различные значения х и находить для них F(х)=Р{X<x}.
- Если
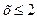, то, очевидно, F(x)=0 в том числе и при х=2 F(2)=P(X<2)=0. - Если
, например, х=3; F(x)=P(X=2)=0,4. очевидно, что и F(4)=P(X<4)=0,4. - Если
, например, х=5; F(x)=P(X=2)+P(X=4)=0,4+0,3=0,7. очевидно, что и F(6)=P(X<6)=0,7. - Если
, например, х=6,123; F(x)=P(X=2)+P(X=4)+P(X=6)=0,4+0,3+0,1=0,8. очевидно, что и F(7)=P(X<7)=0,8. - Если
, например, х=8; F(x)=P(X=2)+ P(X=4)+P(X=6)+P(X=7)==0,8+0,2=1.
|
| . 
|
Заметим, что при подходе слева к точкам разрыва функция сохраняет свое значение, иначе говоря, функция распределения непрерывна слева.
Итак, функция распределения дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующим возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции равна 1.
Свойства функции распределения.
1..
2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси.
3. 
, 
.
4. Р(х1 
Х<x2)=F(x2)-F(x1). (4)
Пример: 
Найти вероятность того, что случайная величина Х примет значение в интервале [2; 5).
Решение: По формулеР(х1 Х<x2)=F(x2)-F(x1). (4)
Р(2 Х<5)=F(5)-F(2)=1-2/3=1/3. (4).
Ответ: 1/3.
Математические операции над случайными величинами.
Определение: Случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какое значение принимает другая случайная величина. В противном случае случайные величины называются зависимыми.
Пример: Суммы выигрыша в двух различных лотереях – независимые случайные величины так как при любом выигрыше в первой лотерее, закон распределения выигрышей по второй лотерее не изменится.
Определим математические операции над дискретными случайными величинами.
Пусть даны две случайные величины: Х и Y
| xi | х1 | х2 | х3 | ….. | xn |
| pi | p1 | p2 | p3 | ….. | pn |
| yj | y1 | y2 | y3 | ….. | ym |
| pj | p1 | p2 | p3 | ….. | pm |
- Произведением kX случайной величины Х на постоянную величину k называется случайная величина, которая принимает значения kxi с теми же вероятностями pi (i=1, …, n).
- Cтепенью m случайной величины Х называется случайная величина Хm, которая принимает значения xim с теми же вероятностями pi (i=1, …, n).
Замечание: так как в ряде случаев одни и те же значения xim могут получаться одними и теми же способами при различных xi, то вероятности таких повторяющихся значений находятся сложением исходных вероятностей.
Пример: Дана случайная величина Х:
| xi | -3 | -2 | |||
| pi | 0,1 | 0,2 | 0,05 | 0,3 | 0,35 |
Найти закон распределения случайных величин 5Х и Х2.
