Ижевск 2011
УДК
Типовые расчеты
по курсу «Высшая математика»
раздел «Теория вероятности и математическая статистика»
П.А. Стаханова, старший преподаватель кафедры ВМ,
Рецензент: М.И. Пономарев, доцент кафедры ВМ.
Типовой расчет содержит 30 вариантов по 14 задач в каждом и предназначен для студентов любых специальностей, изучающих теорию вероятности в рамках общего курса высшей математики. Данный типовой расчет содержит задания, разработанные для усвоения тем «Случайные события, случайные величины».
Объем и характер типового задания соответствует рабочим программам по высшей математике для большинства специальностей ИжГТУ и предназначен для лучшего усвоения студентами курса высшая математика и интенсификации самостоятельных занятий.
В данном пособии представлена также необходимая для выполнения типового расчета теоретическая информация и примеры ее применения.
В конце приводится список литературы, которую можно порекомендовать студентам для изучения данного раздела математики.
© Стаханова П.А. 2011
© Издательство ИжГТУ, 2011
Методические указания к Типовому расчету №1 по теме
«Случайные события, случайные величины».
В соответствии с учебным планом и рабочей программой по По дисциплине «Теория вероятностей, математическая статистика и случайные процессы» направления 230100.62 – «Информатика и вычислительная техника» дневной формы обучения каждый студент должен выполнить два типовых расчета в III семестре 2 курса по курсу теории вероятностей и математической статистики. В данной методичке представлены материалы первого типового расчета по теме «Случайные события, случайные величины».
Типовой расчет №1 «Случайные величины, законы их распределения и числовые характеристики» содержит 14 заданий. Первые четыре задания носят комбинаторный характер; следующее задание связано с непосредственным вычислением вероятности и с применением формул сложения и умножения; задание 7 – геометрическая вероятность; 8 задача связана с применением формулы полной вероятности и формулы Байеса; 9-11 задачи связаны с повторными независимыми испытаниями, три оставшиеся задачи посвящены случайным величинам, законам распределения случайных величин и их числовым характеристикам. Задания контрольной работы охватывают следующие разделы теории вероятностей:
- комбинаторика;
- непосредственное вычисление вероятности случайного события;
- геометрическое определение вероятности;
- формулы суммы и произведения вероятности;
- формулы полной вероятности и формулы Байеса;
– повторные независимые испытания: основные понятия, формула Бернулли, формулы Муавра – Лапласа (локальная и интегральная), формула Пуассона, условия применения указанных формул;
– случайные величины: понятие случайной величины, виды случайных величин (дискретные и непрерывные), способы задания случайных величин (закон распределения, функция распределения и плотность распределения (для непрерывных случайных величин));
– числовые характеристики случайной величины: математическое ожидание, дисперсия, начальные и центральные моменты случайных величин;
– некоторые виды распределений случайных величин: распределения дискретных случайных величин (биномиальное, распределение Пуассона, геометрическое), распределения непрерывных случайных величин (равномерное, показательное, нормальное);
– предельные теоремы теории вероятностей.
Перед выполнением типового расчета необходимо изучить соответствующие разделы литературы (/3/ гл. 5 § 1-3; гл.6 § 1-8; гл. 7 § 1-5; гл. 8 § 1-5, 7, 10; гл. 9 § 1-6; гл. 10 § 1-3; гл. 11 § 1-4, 6; гл. 12 § 2-8; гл. 13 § 1-3) и закрепить с помощью упражнений для самостоятельной работы основные понятия, определения и методы теории вероятностей.
Так же перед решением заданий рекомендуется ознакомиться со всеми примерами, рассмотренными ниже. По каждому заданию типового расчета в методических указаниях приводится основной теоретический материал и разбирается несколько типовых примеров.
Тема 1
Комбинаторика.
Задачи 1-4
Перестановки - это выборки (комбинации), состоящие из n элементов и отличающиеся друг от друга порядком следования элементов.
 ;
;  ;
;
перестановки с повторениями  .
.
Размещениями из n элементов по k элементов будем называть упорядоченные подмножества, состоящие из k элементов, множества, состоящего из n элементов.(порядок важен).  ; размещения с повторениями
; размещения с повторениями  . Одно размещение от другого отличается только не только составом выбранных элементов, но и порядком их расположения.
. Одно размещение от другого отличается только не только составом выбранных элементов, но и порядком их расположения.
Сочетаниями из n элементов по m элементов будем называть любое подмножество, состоящие из m элементов, множества, состоящего из n элементов. (порядок не важен).  ; сочетания с повторениями
; сочетания с повторениями 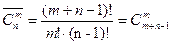 .
.
Одно сочетание от другого отличается только составом выбранных элементов.
Сложная выборка  =
=  .
.
Решения задач:
1. Сколько существует пятизначных чисел, состоящих из цифр 7,8,9, в которых цифра 8 повторяется 3 раза, а цифры 7 и 9 по одному разу.
Решение. Каждое пятизначное число отличается от другого порядком следования цифр, причемn1=1, n2=3, а n3=1, а их количество равна 5, т.е. является перестановкой с повторениями из 5 элементов. Их число находим по формуле (3)  .
.
2. На карточках написаны буквы М,А,Т,Е,М,А,Т,И,К,А. Сколько различных 10-ти буквенных «слов» можно составить из этих карточек? (здесь и далее словом считается любая последовательность букв русского алфавита)
Решение. Перестановка двух букв М, осуществляемая Р2= 2 способами, трех букв А, осуществляемая Р3= 3!=6 способами и перестановка двух букв Т, осуществляемая Р2= 2 способами не меняет составленное из карточек слово.  слов.
слов.
3. Студенты второго курса изучают 10 различных дисциплин. Определить – сколькими способами можно составить расписание на понедельник, если в понедельник планируется поставить 5 пар?
Решение: Каждый вариант расписания представляет собой выборку 5 элементов из 10, причем эти варианты отличаются друг от друга не только выбором этих дисциплин, но и порядком их следования, т.е. является размещением из 10 элементов по 5.  .
.
4. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны?
5. Сколькими способами можно выбрать 4 монеты из четырех пятикопеечных монет и из четырех двухкопеечных монет?
Решение: порядок выбора монет неважен, и примерами соединений могут являться {5,5,5,5}, {2,2,2,2}, {5,2,5,5} и т.д. Это задача о числе сочетаний из двух видов монет по четыре с повторениями.
 способов.
способов.
6. В кондитерской имеется 5 разных сортов пирожных. Сколькими способами можно выбрать набор из 4 пирожных?
Решение: это задача о числе сочетаний из 5 видов пирожных по 4 с повторениями.
 способов
способов
7. Сколько всего чисел можно составить из цифр 1, 2, 3, 4, 5, в каждом из которых цифры расположены в неубывающем порядке?
Решение: это задача о числе сочетаний из 5 цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае.
 ;
;  ;
;  ;
;
 ;
; 
Согласно правилу сложения: 5+15+35+70+126=251 чисел.
Решение:.
8. Решить уравнения а)  ; б)
; б)  .
.
Решение:a)  ;
;  ;
;  ;
;  ;
;



б)  ;
;  ;
;  ;
; 
 .
.
Тема 2






