Описание продукта
Разработка надежных контроллеров на неопределенный растений
Надежные Элементы Управления ™ предоставляет инструменты для анализа и автоматической подстройки систем управления для повышения производительности и надежности. Вы можете создать неопределенность модели, комбинируя номинальная динамика с неопределенными элементами, такими как неопределенный параметр или немоделируемую динамику. Вы можете проанализировать влияние растений неопределенности модели на контроль производительности системы и определения наихудшего сочетания неопределенных элементов. Использование H-бесконечности или мю-методов синтеза, можно создавать контроллеры, максимально надежной стабильности и производительности. Пакет может автоматически настроить как MIMO и SISO робастных регуляторов, в том числе децентрализованной архитектуры управления моделируются в Simulink ®. Вы можете проверить свои разработки на расчете наихудшего усиления и фазы поля и наихудший чувствительность к помехам.
Основные характеристики
• Моделирование систем с неопределенными параметрами или пренебречь динамикой
• Худший случай стабильность и производительность анализа неопределенных систем
• Автоматическая настройка централизованной и децентрализованной систем управления
• Надежный анализ и настройка контроллеров в Simulink
• H-бесконечность и мю-алгоритмы синтезов
• Общее назначение LMI-решателей технико-экономических, минимизация линейных целей, и обобщенной минимизации собственных значений
• Модель снижения алгоритмов, основанные на Hankel singular values
Требования к продукции
Прочная программное обеспечение панели инструментов управления требует, чтобы вы установили системы управления Toolbox ™.
Моделирование неопределенности
В основе надежного контроля является концепция неопределенной системы LTI. Модель неопределенность возникает тогда, когда система получает или других параметров, точно не известно, и может изменяться в заданном диапазоне. Примеры реальных параметров неопределенности включают неопределенность полюсов и нулей местах и неопределенные выгоды. Вы также можете неструктурированных неопределенностей, под которой понимается комплекс изменений параметров удовлетворяет данной границы величины.
С Надежным программным обеспечением панели инструментов управления вы можете создать неопределенность LTI моделей, как MATLAB ® объекты, специально предназначенные для надежных систем управления. Вы можете строить модели сложных систем, комбинируя модели подсистем использованием сложения, умножения и деления, а также с системой управления Toolbox команды, такие как обратная связь и LFT.
Пример: ACC Benchmark Problem
Например, рассмотрим два корзину "АСС Benchmark" системы [13], состоящий из двух трения тележки, соединенных пружиной показано в следующем.
ACC Benchmark Problem

Система Блок-схема модели будет показано ниже, где отдельные тележки имеют соответствующие функции передачи.

Параметры m 1, m 2, и k еще не определились, равно один плюс или минус 20%:
m1 = 1 ± 0,2
m2 = 1 ± 0,2
= 1 ± 0,2
"АСС Benchmark" Две корзины Система Блок-схема y1 = P(s) u1

Верхняя пунктирная линия-блок имеет передаточную функцию матрицы F (s): 
Этот код создает неопределенность P модель системы, указанный ниже:
% Создаем неопределенный реальных параметров M1, M2, и к
m1 = мочевинных ('m1', 1, 'процент', 20);
m2 = мочевинных (М2, 1, 'процент', 20);
к = мочевинных ('к' 1, 'процент', 20);
S = ЗПК ("S");% создать переменную Лапласа с
G1 = сс (1 / с ^ 2) / m1;% корзину 1
G2 = сс (1 / с ^ 2) / м2;% корзину 2
% Теперь построить F и P
F = [0; G1] * [1 -1] + [1, -1] [0, G2];
P = LFT (F, А)% закройте петли с ключом k
Переменная Р SISO неопределенном состоянии-пространстве (USS) объект с четырьмя государствами и тремя неопределенными параметрами, М1, М2, и к. Вы можете восстановить номинальные растение с командой
ЗПК (P.nominal)
который возвращается
Zero / полюс / прибыль:
1
--------------
s^2 (s^2 + 2)
Если неопределенность модели P (S) имеет отрицательный LTI контроллер обратной связи

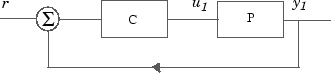
Затем вы можете сформировать контроллером и замкнутой системы y 1 = T (s) u 1 и перейдите к шагу реакция замкнутой системы на интервале времени от t=0 to t=0.1 для Монте-Карло случайная выборка из пяти комбинаций трех неопределенных параметров k, m1, and m2 с помощью этого кода:
C=100*ss((s+1)/(.001*s+1))^3 % LTI controllerT=feedback(P*C,1); % closed-loop uncertain systemstep(usample(T,5),.1);
В результате участок приведен ниже.
Монте-Карло Отбор Шаг ответ Неопределенная Системы

Наихудший производительности
• Чтобы быть надежной, ваша система управления должна соответствовать вашей стабильности и производительности для всех возможных значений неопределенных параметров. Монте-Карло, параметр выборки по usample могут быть использованы для этой цели, как показано в Монте-Карло Отбор Шаг ответ Неопределенная система, но методы Монте-Карло по своей природе попало. В методах Монте-Карло, возможно, потребуется принять невозможно большого количества образцов, прежде чем вы нажмете на или рядом с наихудшему параметру комбинации.
• Прочная программное обеспечение панели инструментов управления дает вам мощный набор команд, надежность анализа, который позволяет непосредственно рассчитать верхнюю и нижнюю границы в самом худшем случае производительность без случайной выборки.
Наихудший команд Надежность анализа:
loopmargin - Комплексный анализ обратной связи
loopsens - Чувствительность функции обратной связи
ncfmargin - Нормализованная маржа взаимно стабильность петли обратной связи
robustperf - Надежная производительность неопределенных систем
robuststab - Стабильность поля неопределенных систем
wcgain - Наихудший случай усиления неопределенности системы
wcmargin - Наихудший случай усиления / фазы поля для обратной связи
wcsens - Наихудший случай чувствительности функции обратной связи
Пример: ACC Two-Cart Benchmark Problem
• Возвращаясь к примеру: ACC Проблема Benchmark, замкнутой системы является:
T = обратная связь (P * C, 1);% с обратной связью неопределенной системы
Эта неопределенность пространства состояний модели Т состоит из трех неопределенных параметров, к, M1 и M2, каждая из которых равна 1 ± 20% неопределенной изменчивости. Для анализа того, замкнутая система Т надежно стабильным для всех комбинаций значений этих трех параметров, вы можете выполнить команду:
• [StabilityMargin, Udestab, ОТЧЕТ] = robuststab (T);
• ОТЧЕТ
• Это отображает отчет:
• Неопределенность Система надежно устойчива к моделируемой неопределенности.
• - Он может переносить до 311% моделируемых неопределенности.
• - дестабилизирующий сочетание 500% моделируемых неопределенность существует,
• вызывает нестабильность на 44,3 рад / с.
• В докладе говорится, что система управления является устойчивой для всех параметров изменения в ± 20% диапазона, и, что наименьшее дестабилизирующих сочетание реальные изменения в значениях к, M1 и M2 имеет размеры где-то между 311% и 500% больше чем на ± 20%, т.е. в пределах ± 62,2% и ± 100%. Значение Udestab возвращает оценку 500% дестабилизирующих комбинации изменения параметров:
• Udestab =
• к: 1.2174e-005
• m1: 1.2174e-005
• м2: 2,0000.
Неопределенность замкнутой системы Боде участки

•
• У вас есть удобный запас в размере от 311% до 500% больше, чем ожидалось ± 20% вариаций параметров до замкнутого контура идет нестабильно. Но сколько можно замкнутой производительности ухудшается для изменения параметров вынужден лежать строго в рамках ожидаемого ± 20% диапазона? Следующий код вычисляет наихудший пик прироста T, и оценивает частоту и значения параметра, при котором максимальный прирост происходит:
• [PeakGain, ВКУ] = wcgain (T);
• Twc = usubs (T, ВКУ);
•% худшем случае замкнутой системы T
• Торговые = usample (Т, 4);
•% 4 случайных выборок неопределенной системы T
• bodemag (TWC, «р», Торговые, {}.5,50 "B-".);% У Боде
• Легенда («T_ {} туалет - наихудший,...
• «T_ {} рандов - случайная выборка, 3);
• В результате сюжет показали в Неопределенная замкнутой системы Боде участки.




