Нет, т.к. это является необходимым условием. при (0,0) =0 это >=0 Отв:да (я точно не уверена в том что >=0)

35. f(x,y)=x⁶y⁴ (0,0)

x=0 y=0

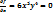
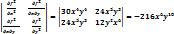при (0,0) =0 это >=0 Отв:да (я точно не уверена в том что >=0)

36. f(x,y)=xy⁴ (0,0)

x=0 y=0

при (0,0) = 0 Отв: да (точно не уверена)

37. f(x.y)=x²-y² (o,o)

x=0 y=0

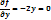
=-4 <0 точек нет Ответ: нет

38. а) F’_x=2x F’_y=2y

В точке (1,1) первые производные данной функции не обращаются в ноль, следовательно точка (1,1) не является точкой локального экстремума (не выполняется необходимое условие).

б) Дано уравнение связи x+y=2. Y=2-x

f= x²+(2-x)²=2x²-4x+4

f^’=4x-4=0 x=1 при х=1 у=2-1=1

39. Рассмотрим 3 случая. 1) х-1>0 2)x-1<0 3) x=0

Аналогично как в предыдущих.

Ответ: -3

40. Ответ: наим 3²=9

Наиб 7²=49

Ответ: наим 3²=9

Наиб 7²=49

Наиб 7²=49

 

Теорема о равенстве смешанных производных

Если производные и сущест­вуют в некоторой окрестности точки М(х₀, у₀) и непрерывны в самой точке М, то имеет место равенство

(М)=(М)

 

Формула Тейлора для функции нескольких переменных с остаточным членом в форме Лагранжа.

Пусть функция f(х) имеет (п +1) производных в E-окрестности точки х₀. Тогда для любой точки х из этой окре­стности найдется точка с, расположенная между точками х и х₀, для которой выполняется следующая формула

f(х) = T(х) +

где T(x)- п-й многочлен Тейлора функции f(х) в точке х₀. - остаточный член в форме Лагранжа

 

Локальные экстремумы функций нескольких переменных.

Точка М называется точкой локального минимума функции у=f (x), если существует такая окрестность М, что в любой точке X этой окрестности выполняется неравенство f(М) <= f(X).

Аналогично точка М называется точкой локального максимума функции y = f (X), если существует такая окрестность М, что в любой точке X этой окрестности выполняется неравенство f(М) >= f(X).

Точки локальных минимумов и максимумов функции у=f(X) называются точками локальных экстремумов данной функции

 

Необходимое условие локального экстремума функций нескольких переменных.

Теорема. Пусть функция f(x₁,..., x_m) определена в некоторой окрестности т. , дифференцируема в точке М₀, и имеет в этой точке локальный экстремум, тогда все частные производные первого порядка функции f в т. М₀ равны нулю:

 

Достаточное условие локального экстремума функций нескольких переменных.

Пусть в некоторой окрестности стационарной точки определены частные производные второго порядка функции f(x₁,..., x_m), которые являются непрерывными в т. М₀. Если в этой точке второй дифференциал d² f(M₀) является знакоопределенной квадратичной формой от dx₁,..., dx_m, то в т. М₀ функция имеет локальный экстремум (локальный максимум, если d² f(M₀) отрицательно определена, и локальный минимум, если d² f(M₀) положительно определена), если же d² f(M₀) знакопеременна, то в т. М₀ экстремума нет.

 

Условный экстремум.

Пусть у= f(X) функция с областью определения D(f) и пусть S - подмножество в D(f) (т.е. S является частью в D(f). Точка A принадлежит S называется точкой условного минимума функции f, если сущест­вует такая окрестность точки А, что для любой точки В, лежащей од­новременно и в этой окрестности точки А и множестве S, верно нера­венство f(A)<= f(B).

Аналогично точка А принадлежит S называется точкой условного максимума функции f, если существует такая окрестность точки А, что для любой точки В, лежащей в этой окрестности и в S, верно неравенство f(A)>=f(B).

Общее название для условных минимумов и максимумов — условные экстремумы.

Метод Лагранжа.

Пусть функции f и g₁ …g_s определены и имеют непрерывные ча­стные производные в окрестности точки х* причем, векторы

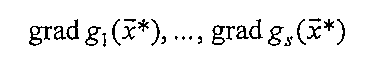
линейно независимы. Тогда если х* - точка условного экстремума функции f при условиях

то найдутся числа ʎ₁ …ʎ_s для ко­торых x* - стационарная точка функции

Функция L называется функцией Лагранжа, а числа множителями Лагранжа.