Первообразная.
Ф-я F(x) называется первообразной ф-и f(x) на множестве D, если для любого х из D:F’(x)=f(x).
Если F(x) первообрзная ф-и f(x) на мн-ве D, то любую другую первообразную этой ф-и можно получить по формуле: Ф(х)=F(x)+c при некотором значение с.
Док-во. Пусть F(x) – первообразная f(x), x принадлежит D: F’(x)=f(x).
Пусть Ф(х) – другая первообразная f(x), x принадл. D: Ф’(x)=f(x).
Составим ф-ю φ(х)=Ф(х)-F(х) – дифференцируема на мн-ве D → φ'(х)= Ф’(х)-F’(х)=f(x)-f(x)=0. По св-м ф-и, дифференцируемой на D → φ(х)=соnst.=c → Ф(х)-F(х)=с=const → Ф(х)=F(х)+с, что и т.д.
Неопределенный интеграл
Опр. Совокупность всех первообразных для ф-и f(x) на множестве наз. Неопределенным интегралом этой функции. ∫f(x)dx=F(x)+c, f(x)-подинтегральная ф-я,f(x)dx – подинтегральное выражение.
Свойства неопределенного интеграла
1)[f(x)dx]’=f(x)
док-во: ∫f(x)dx=F(x)+c(по опр.), (∫f(x)dx)’= (F(x)+c)’=F’(x)=f(x)
2) d[f(x)dx] = f(x)dx
док-во: по опр. дифференциала: d[f(x)dx] = (f(x)dx)’dx=f(x)dx
3)∫dF(x)=F(x) +c
док-во: ∫dF(x)=∫F’(x)dx=∫f(x)dx=F(x)+c.
4)Постоянный множитель можно выносить за знак неопред. Интеграла:
∫kf(x)dx=k∫f(x)dx,x є D, k є R.
док-во: покажем, что k∫f(x)dx – совокупность первообразных для ф-и k*f(x):
По св-ву производной: (k∫f(x)dx)’=k*(∫f(x)dx)’=k*f(x).
5)∫[f(x)+(-)g(x)]dx = ∫f(x)dx +(-)∫g(x)dx/
Док-во: докажем, что ∫f(x)dx +(-)∫g(x)dx – первообразная для ф-и [f(x)+(-)g(x)]:
По св-ву производной: [f(x)+(-)g(x)]’= [∫f(x)dx]’ +(-)[∫g(x)dx]’= f(x)+(-)g(x), что и т.д.
Табличные интегралы.
Таблица интегралов
1) ∫ 0 dx = C = const 11) ∫dx/(√1-x2 )= arcsin x + C = - arccos x + C
2) ∫dx = x + C 12) ∫dx/(1+x2) = arctg x + C = - arcctg x + C
3) ∫xadx = xa+1/(a+1) + C, 13) ∫tgxdx = - ln |cosx| + C
a≠ -1 14) ∫ctgxdx = ln |sinx| + C
4) ∫dx/x = ln|x| + C 15) ∫ dx/(√a2- x2)=arcsinx/a +C=-arccos x/a + C
5) ∫exdx = ex + C 16) ∫dx/(a2+x2) = (1/a)arctg x/a + C=-(1/a)arcctg x/a + C
6) ∫axdx = ax/lnx + C 17) ∫dx/(x2–a2) = (1/2a) ln |(x-a)/(x+a)| + C
7) ∫cosx dx = sinx + C 18) ∫dx/(a2-x2) = (1/2a) ln |(x+a)/(x-a)| + C
8) ∫sinxdx = - cosx + C 19) ∫dx/(√x2+A) = ln |x + (√x2+A)| + C
9) ∫dx/cos2x = tgx + C
20) ∫(√x2+A)dx = (x/2)(√x2+A) + (A/2) ln |x+(√x2+A)|+C
10) ∫dx/sin2x = - ctgx + C
21) ∫ (√a2- x2)dx = (a2/2) arcsin x/a + (x/2) (√a2- x2) + C
Метод замены переменной или метод подстановки
∫f(x)dx, x Î D
Пусть x = φ(t), t Î T, φ(t) – дифференцируема на T и имеет обратную функцию
Докажем, что ∫ f(x)dx = ∫f(φ(t)) • φ’(t)dt, т. е. докажем, что ∫f(x)dx – первообразная f(φ(t))•φ’(t)
(∫f(x)dx)t’(по правилу дифференцирования сложной функции) = (∫f(x)dx)x’ • x’t = f(x)•φ’(t) = f(φ(t))•φ’(t)
∫ f(x)dx = ∫f(φ(t)) • φ’(t)dt – формула замены переменной в неопределенном интеграле
Метод интегрирования по частям
Пусть u = u(x), v = v(x) – дифференцируемы на D
d(u•v) = du•v + u•dv Þ ∫ d(u•v) = ∫du•v + ∫u•dv Þ u•v = ∫v•du + ∫u•dv Þ
∫u•dv = u•v - ∫v•du – формула интегрирования по частям
Применение данной формулы:
1. Pn (x)•φ(x)dx; Pn (x) – многочлен n-ой степени
а) φ(x) = sin ax u = Pn (x); dv = φ(x)dx
cos ax
eKx
b) φ(x) = обратные тригонометрические функции u = φ(x); dv = Pn (x)dx
logax
2. ekx•sin ax dx в этом случае любой из множителей можно принять
ekx•cos ax dx за u
11. Формула Ньютона-Лейбница:
Пусть функция y=f(x) непрерывна на отрезке [a;b] и F(x)- первообразная для f(x). Тогда:
∫(a по b) f(x)dx= F(b)-F(a)
12. Формула замены переменной в определенном интеграле:
Пусть функция x=A(t) определена и дифференцируема на промежутке T и X – множество ее значений, на котором определена функция f(x). Тогда если F(x) – первообразная для f(x) на X, то F(A(t))- первообразная для f(A9t))A’(t) на T, т.е. на множестве Т выполняется равенство:
∫f(x)dx│x=A(t) = ∫f(A(t))A’(t)dt
13. Формула интегрирования по частям для определенного интеграла:
Пусть u(x) и v(x) – две дифференцируемые функции на промежутке X. Тогда на Х выполняется формула интегрирования по частям:
∫udv=uv-∫vdu
14. Определение несобственного интеграла с бесконечным верхним пределом:
Пусть функция y=f(x) интегрируема на каждом конечном отрезке [a;b] (b>a). Тогда за несобственный интеграл принимают:
∫(a по +∞)f(x)dx= lim b→∞ ∫(а по b)f(x)dx
,когда b стремится к бесконечности.
15. Определение несобственного интеграла с бесконечным нижним пределом:
По аналогии с верхним вопросом можно рассмотреть несобственный интеграл с бесконечным нижним пределом, а именно:
∫(b по -∞)f(x)dx= lim a→-∞ ∫(b по a)f(x)dx
16. Определение несобственного интеграла от неограниченной функции на ограниченном промежутке:
17. Пространство Rⁿ
18. Расстояние в Rⁿ. Свойства расстояния.
В пространстве Rⁿ, где n>3, о расстоянии можно говорить лишь в условном смысле, так как точки в Rⁿ не имеют непосредственного геометрического истолкования. Расстояние определяется формулой:
ρ (p,q)= │p-q│=√(x1’- x1”)²+…+(xⁿ’-xⁿ”)²
, где p=(x1’, x2’, …, xⁿ’) и q=(x1”, x2”, …, xⁿ”) – две произвольные точки из Rⁿ.
Свойства:
1) ρ (p,q)>0, елси p ≠ q, и ρ (p,p)=0;
2) ρ (p,q)= ρ (q,p);
3) ρ (p,q)+ ρ (q,r)>= ρ (p,r), каковы бы ни были точки p,q и r. (свойство треугольника).
19. Окрестность точки в Rⁿ.
Пусть pₒ- точка в Rⁿ и ε – положительное число. Открытым шаром, или просто шаром радиуса ε с центром в pₒ называется множество всех точек, расстояние которых от pₒ меньше ε:
{p € Rⁿ │ ρ (pₒ,p)< ε}.
Шар радиуса ε с центром pₒ обозначается B(pₒ, ε) или U3(pₒ). Множество U3(pₒ) называют
ε–окрестностью точки pₒ.
20. Внутренние и граничные точки множества:
Пусть Х – множество в пространстве Rⁿ. Точка р называется:
-Внутренней точкой множества Х, если она содержится вместе с некоторой своей
ε–окрестностью;
-Внешней точкой по отношению к Х, если она является внутренней для дополнения Х в Rⁿ;
-Граничной точкой для Х, если она не является ни внутренней ни внешней точкой для Х, иначе говоря, если любая ее окрестность содержит как точки, принадлежащие Х, так и точки, не принадлежащие Х.
21. Открытые и замкнутые множества.
Множество X называется открытым, если все его точки внутренние.
Множество X называется закрытым, если оно содержит все свои граничные точки.
22. Изолированные и предельные точки множества.
Пусть X - множество в Rn. Точка p0 называется предельной для X, если в любой
ε-окрестности точки p0 имеются точки множества X, отличные от p0.
При этом сама точка p0 может как принадлежать, так и не принадлежать множеству X.
Точка p0 Î X называется изолированной точкой множества X, если у нее существует
ε-окрестность, в которой никаких других точек из X, кроме p0, нет.
Ясно, что любая точка множества Х является либо изолированной, либо предельной
для Х.
23. Ограниченные множества.
Множество X 
Rn называется ограниченным, если оно целиком содержится в некотором шаре.
Нетрудно показать, что ограниченность множества Х означает, что существует такое число C>0, что координаты любой точки p=(x1,x2,…,xn) из Х по модулю не превосходят С: |x1| 
.
24. Сходимость последовательности точек в Rn, ее эквивалентность покоординатной сходимости.
Пусть 
– последовательность точек в Rn. Мы говорим, что эта последовательность сходится к точке p0, если числовая последовательность 
имеет предел 0.
Пусть p1=(x1,y1), p2=(x2,y2),…- последовательность точек в 
. Мы скажем, что эта последовательность сходится к точке p0=(x0,y0), если числовая последовательность x1,x2,… сходится к числу x0, а числовая последовательность y1,y2,… - к числу y0.
25. Функция нескольких переменных.
?
26. Поверхности (линии) уровня функции нескольких переменных.
Линией уровня функции называют линию f(x,y)=C на координатной плоскости, в точках которой функция f принимает постоянное значение C.
При n>2 следует говорить не о линиях, а о множествах уровня. Множество уровня имеет уравнение f(
и истолковывается как “ поверхность” в 
27. Предел функции нескольких переменных.
Пусть на множестве X Rn задана функция f(p) и пусть p0 – предельная точка для Х. Число a называется пределом функции f в точке p0, если для любой сходящейся к p0 последовательности , где все pn 
p0, соответствующая числовая последовательность 
сходится к числу а.
Запись: 
, или в координатной форме: 
28. Непрерывность функции нескольких переменных.
Функция f(p), определенная на множестве X Rn, называется непрерывной
в точке р0 Î X, если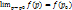 
, или же, если p0 – изолированная точка множества Х.
Функция f(p), определенная на множестве X Rn, называется непрерывной на этом множестве, если она непрерывна в каждой точке множества Х.
29. Свойства функций, непрерывных на замкнутом ограниченном множестве: ограниченность, достижение наибольшего и наименьшего значений.
Если числовая функция f от n переменных задана на ограниченном и замкнутом множестве Х Rn, то она ограничена на этом множестве.
Если числовая функция f от n переменных задана на ограниченном и замкнутом множестве Х Rn, то существует точка p0 Î X, в которой f принимает свое наименьшее значение, и точка q0 Î X, в которой f принимает свое наибольшее значение на Х.
30. Частные производные функции нескольких переменных.
Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения частного приращения функции к приращению соответствующей независимой переменной, когда это приращение стремится к нулю.
Частные производные функции z=f(x,y) в точке (x0,y0) обозначаются так:
z’x, dz/dx, f’x(x0,y0) – производная по x;
z’y, dz/dy, f’y(x0,y0) – производная по y.
31. Пусть D из Rn – область в Rn, содержащая с каждой своей точкой (x1, x2, …., xn) и все точки вида (tx1, tx2, …., txn) при t>0 функция f(x1, x2, …., xn) с такой областью определения D называется однородной степени λ, если для любого t>0 выполнятся равенство f (tx1, tx2, …., txn)=tλ f(x1, x2, …., xn).
Да, является. 2 степени.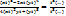 
=t2
32. Пример однородной функции степени 3:
F (x,y)=x2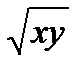 
F (tx, ty)=t2x2√(tx*ty)=t3 F (x,y)
33. f (tx1, tx2,tx3)=tλ f(x1, x2, x3). u= f(x,y,z)
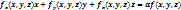
34. Пусть z=f(x;y) определена в некоторой области D и точка М(х0;у0) – внутренняя точка D (М принадлежит D), тогда данная функция в данной точке будет иметь локальный минимум (максимум), если найдется e - окрестность точки М, что для всех внутренних точек этой окрестности, отличных от М(х0;у0) выполняются неравенства:
f(x;y)>f(х0;у0) – min
f(x;y)<f(х0;у0) – max
