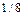| № п/п | Примеры ПП 16 9. Текстовые задачи разного содержания на нахождение наибольшего и наименьшего значения величин |
| №24 |  Площадь поверхности сферы равна Площадь поверхности сферы равна 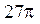 . Какова высота цилиндра наибольшего объема, вписанного в эту сферу?
Обозначим высоту цилиндра . Какова высота цилиндра наибольшего объема, вписанного в эту сферу?
Обозначим высоту цилиндра 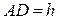 , ,  . По условию . По условию 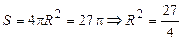 , , 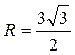 .
Из .
Из  : :  . Объем цилиндра . Объем цилиндра 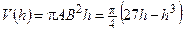 . По смыслу задачи . По смыслу задачи  , т.е. , т.е. 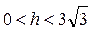 . Исследуем функцию . Исследуем функцию 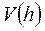 на этом интервале. Производная на этом интервале. Производная 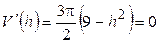 при при 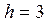 , вблизи этого значения , вблизи этого значения 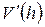 меняет знак с + на –, значит при этой высоте объем цилиндра будет наибольшим. меняет знак с + на –, значит при этой высоте объем цилиндра будет наибольшим.
|
| №25 | Владелец фабрики установил, что если он будет продавать свои изделия по цене 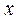 руб., то его годовая прибыль руб., то его годовая прибыль  составит составит 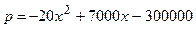 руб. Определите руб. Определите 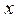 , при котором прибыль будет максимальной. , при котором прибыль будет максимальной.
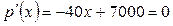 при при 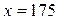 , при этой цене прибыль будет максимальной. , при этой цене прибыль будет максимальной.
|
| пп 16. I. исследование функций | |||||||||||||||||||||||||||||||||
| № п/п | ЗАДАЧИ | ||||||||||||||||||||||||||||||||
| ПП16.I №1 | Найдите интервалы монотонности и точки экстремума функции  .
РЕШЕНИЕ:
Функция .
РЕШЕНИЕ:
Функция 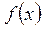 не определена при не определена при  . .
 , , 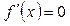 при при 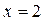 . .
Функция | ||||||||||||||||||||||||||||||||
| ПП16.I №2 | Найдите экстремумы функции 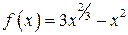 . .
 , , 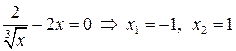 , , 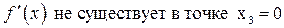 . .
Вид графика функции
| ||||||||||||||||||||||||||||||||
| ПП16.I №3 | Исследуйте функцию 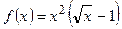 на возрастание (убывание) и экстремумы. на возрастание (убывание) и экстремумы.
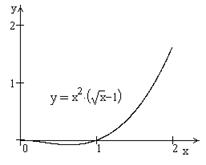 РЕШЕНИЕ:
Функция РЕШЕНИЕ:
Функция 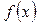 определена для определена для  . Производная функции . Производная функции  обращается в ноль при
обращается в ноль при 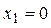 и и 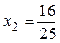 , , 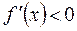 при при  , ,  при при 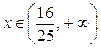 , то есть в точке , то есть в точке 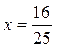 функция принимает минимальное значение. функция принимает минимальное значение.
| ||||||||||||||||||||||||||||||||
| ПП16.I №4 | Исследуйте функцию 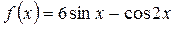 на возрастание (убывание) и экстремумы.
РЕШЕНИЕ:
Производная функции на возрастание (убывание) и экстремумы.
РЕШЕНИЕ:
Производная функции 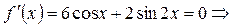 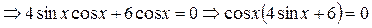 . .
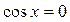 при при 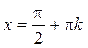 ,
второй множитель положителен при любых ,
второй множитель положителен при любых 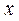 .
Знак производной совпадает со знаком .
Знак производной совпадает со знаком 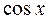 :
при :
при 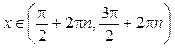 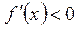 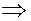 функция убывает; при функция убывает; при 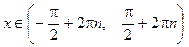 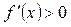 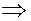 функция возрастает,
в точках функция возрастает,
в точках  достигается максимальное достигается максимальное  ,
а в точках ,
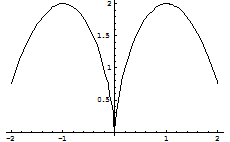
а в точках 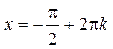 – минимальное – минимальное 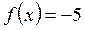 значения функции значения функции 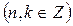 . .
| ||||||||||||||||||||||||||||||||
| ПП16.I №5 | Исследуйте функцию 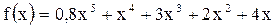 на возрастание (убывание) и экстремумы.
РЕШЕНИЕ:
Производная функции представляет собой многочлен, который мы преобразуем следующим образом: на возрастание (убывание) и экстремумы.
РЕШЕНИЕ:
Производная функции представляет собой многочлен, который мы преобразуем следующим образом:
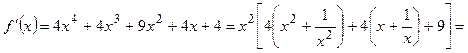
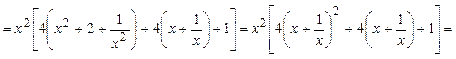
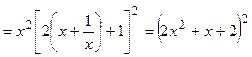 , откуда видно, что , откуда видно, что 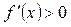 при любых при любых  , значит, функция возрастает для всех , значит, функция возрастает для всех 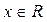 и экстремумов не имеет. и экстремумов не имеет.
| ||||||||||||||||||||||||||||||||
| ПП16.I №6 | Исследуйте функцию 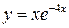 и постройте её график.
РЕШЕНИЕ:
1) и постройте её график.
РЕШЕНИЕ:
1) 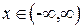 , , 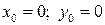 - точка пересечения с осями.
2) f (x) – непрерывна всюду - точка пересечения с осями.
2) f (x) – непрерывна всюду 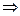 вертикальных асимптот нет. вертикальных асимптот нет.
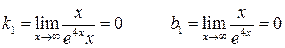
 - наклонная (горизонтальная) асимптота при - наклонная (горизонтальная) асимптота при 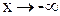  наклонных асимптот при наклонных асимптот при 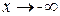 нет.
3) нет.
3)  , , 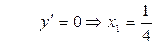 .
4) .
4) 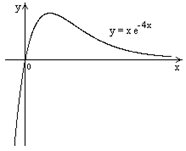 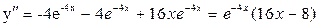 , , 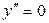 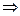  . .
Вид графика функции |
| ПП16.I №7 | Сколько раз график функции 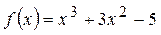 пересекает ось пересекает ось  ?
РЕШЕНИЕ:
Функция определена для всех ?
РЕШЕНИЕ:
Функция определена для всех 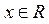 ,
не обладает определенной четностью,
непериодическая. ,
не обладает определенной четностью,
непериодическая.
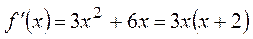 ; ; 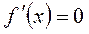 при при  и и 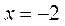 .
График функции .
График функции  пересекает ось пересекает ось  в одной точке в одной точке 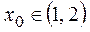 .
Построим схему. .
Построим схему.

| |||||||||||||||||||||||
| ПП16.I №8 | Исследуйте функцию  и постройте её график.
РЕШЕНИЕ:
1) Область определения функции: и постройте её график.
РЕШЕНИЕ:
1) Область определения функции: 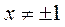 ; эти точки являются точками разрыва функции; при ; эти точки являются точками разрыва функции; при 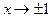 функция функция  ; при ; при 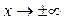 , , 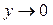 . .
 2) Функция нечетная: 2) Функция нечетная: 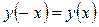 . Построим график для . Построим график для  и отобразим его нечетным образом относительно начала координат.
3) Точка пересечения с осью и отобразим его нечетным образом относительно начала координат.
3) Точка пересечения с осью  определяется условием определяется условием
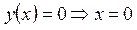 , , 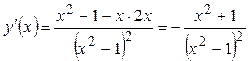 , , 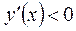 для всех для всех 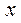 из области определения, т.е. функция является убывающей и не имеет экстремумов. из области определения, т.е. функция является убывающей и не имеет экстремумов.
|
| ПП16.I №9 | Исследуйте функцию  и постройте её график.
РЕШЕНИЕ:
1) Функция определена всюду, кроме точки и постройте её график.
РЕШЕНИЕ:
1) Функция определена всюду, кроме точки  .
График функции имеет вертикальную асимптоту .
График функции имеет вертикальную асимптоту 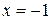 .
2) Точка пересечения с осями: .
2) Точка пересечения с осями: 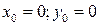 .
3) Выясним, существуют ли наклонные асимптоты. Вычислим пределы: .
3) Выясним, существуют ли наклонные асимптоты. Вычислим пределы:
 ; ;
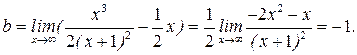
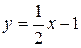 является наклонной асимптотой.
4) Находим производную: является наклонной асимптотой.
4) Находим производную: 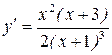 . Знак производной определяется знаком дроби . Знак производной определяется знаком дроби 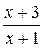 . При . При 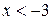 и и 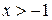 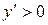 , а при , а при  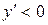 . Интервалы возрастания есть . Интервалы возрастания есть  и и 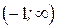 ; интервал убывания ; интервал убывания 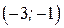 . В области определения функции производная существует всюду и обращается в ноль при . В области определения функции производная существует всюду и обращается в ноль при 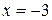 и и 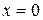 . При . При 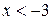 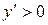 , а при , а при  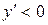 . Следовательно, точка . Следовательно, точка 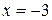 является точкой максимума. Находим значение функции при является точкой максимума. Находим значение функции при 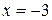 : :  При переходе через другую критическую точку При переходе через другую критическую точку 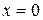 производная знак не меняет, т.е. производная знак не меняет, т.е. 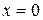 не является точкой экстремума.
5) Находим вторую производную не является точкой экстремума.
5) Находим вторую производную  . Видим, что . Видим, что  при при 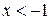 , интервал , интервал 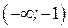 является областью выпуклости. является областью выпуклости.  также при также при 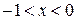 - это тоже область выпуклости; - это тоже область выпуклости; 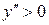 при при 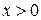 - это область вогнутости.
В области определения функции - это область вогнутости.
В области определения функции  существует всюду; существует всюду; 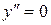 при при 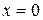 . Так как при переходе через эту точку . Так как при переходе через эту точку  меняет знак, то меняет знак, то 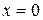 есть абсцисса точки перегиба. Находим есть абсцисса точки перегиба. Находим 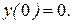
График | ||||||||||||||||||||||||||||||||||||||||
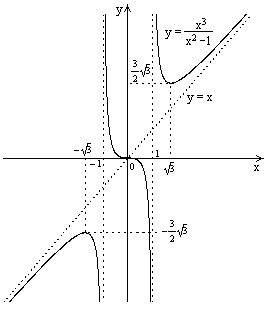
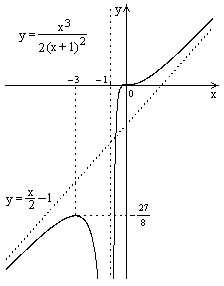
| ПП16.I №10 | Исследуйте функцию 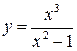 и постройте её график.
РЕШЕНИЕ:
1). Функция определена всюду, кроме точек и постройте её график.
РЕШЕНИЕ:
1). Функция определена всюду, кроме точек 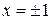 . Точки пересечения графика с координатными осями: . Точки пересечения графика с координатными осями:  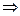  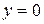 - точка пересечения с осями.
2). Функция нечетная, - точка пересечения с осями.
2). Функция нечетная, 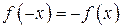 , график симметричен относительно начала координат, достаточно исследовать функцию при , график симметричен относительно начала координат, достаточно исследовать функцию при  .
3). Точка .
3). Точка  является точкой разрыва II-рода, график функции имеет вертикальную асимптоту является точкой разрыва II-рода, график функции имеет вертикальную асимптоту  , , 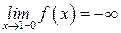 , ,  . Выясним, существуют ли наклонные асимптоты. Вычислим пределы: . Выясним, существуют ли наклонные асимптоты. Вычислим пределы:  ; ; 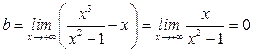 , т.е., , т.е.,  является правой наклонной асимптотой (и левой, так как при операции симметрии прямая переходит сама в себя).
4). Находим производную: является правой наклонной асимптотой (и левой, так как при операции симметрии прямая переходит сама в себя).
4). Находим производную:  . Знак производной определяется знаком . Знак производной определяется знаком 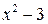 . При . При  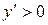 , а при , а при  и и  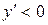 . Интервал возрастания - . Интервал возрастания -  ; интервалы убывания - ; интервалы убывания - 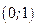 и и  . В области определения функции производная обращается в нуль при . В области определения функции производная обращается в нуль при 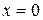 и и  . При . При  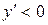 , а при , а при  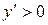 . Следовательно, точка . Следовательно, точка  является точкой минимума. Находим значение функции при является точкой минимума. Находим значение функции при  : :  . При переходе через критическую точку . При переходе через критическую точку 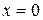 производная знак не меняет, т.е. производная знак не меняет, т.е. 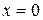 не является точкой экстремума.
5). Находим вторую производную не является точкой экстремума.
5). Находим вторую производную 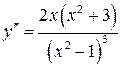 . Видим, что . Видим, что  при при  , на интервале , на интервале 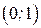 график функции выпуклый вверх. При график функции выпуклый вверх. При  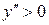 - график функции выпуклый вниз.
В области определения функции - график функции выпуклый вниз.
В области определения функции  существует всюду; существует всюду; 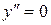 при при 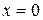 . Так как при переходе через эту точку . Так как при переходе через эту точку  меняет знак, то меняет знак, то 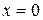 есть абсцисса точки перегиба. Находим есть абсцисса точки перегиба. Находим 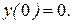
График
| ||||||||||||||||||||||||||||||||||||||||
| ПП16.I №11 | Исследуйте функцию  и постройте её график.
РЕШЕНИЕ:
1). Так как функция периодична с основным периодом и постройте её график.
РЕШЕНИЕ:
1). Так как функция периодична с основным периодом 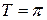 , достаточно исследовать ее поведение на промежутке, длиной равном периоду, например, на , достаточно исследовать ее поведение на промежутке, длиной равном периоду, например, на 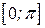 . Арктангенс определен для всех значений аргумента, поэтому областью определения сложной функции . Арктангенс определен для всех значений аргумента, поэтому областью определения сложной функции 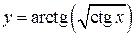 будут промежутки оси будут промежутки оси 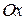 , на которых , на которых 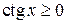 , т.е., для промежутка , т.е., для промежутка 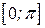 это будет это будет 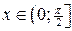 . Для . Для  , область значений , область значений 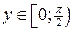 . Точки пересечения графика с координатными осями: при . Точки пересечения графика с координатными осями: при 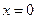 котангенс не определен, точек пересечения с осью котангенс не определен, точек пересечения с осью 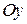 нет. Точки пересечения с осью нет. Точки пересечения с осью 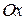 находим, решая уравнение находим, решая уравнение 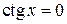 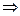 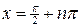 .
2). Четностью или нечетностью функция не обладает.
3). Точка .
2). Четностью или нечетностью функция не обладает.
3). Точка  не является точкой разрыва, так как не является точкой разрыва, так как 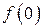 не определена, не определена, 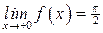 . Поскольку на каждом периоде график . Поскольку на каждом периоде график 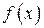 лежит в конечной области плоскости лежит в конечной области плоскости 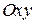 , асимптот у графика существовать не может.
4). Найдем производную: , асимптот у графика существовать не может.
4). Найдем производную:  . Для . Для 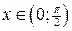 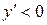 , , 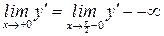 , т.е., на каждом отдельном промежутке области определения функция монотонно убывает.
5). , т.е., на каждом отдельном промежутке области определения функция монотонно убывает.
5). 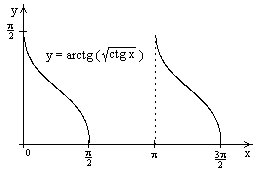 Найдем вторую производную Найдем вторую производную  . Корень уравнения . Корень уравнения 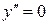 на на 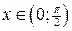 - - 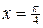 . При . При 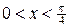  график функции выпуклый вниз, при график функции выпуклый вниз, при 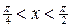 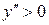 - график функции выпуклый вверх. Точка графика - график функции выпуклый вверх. Точка графика 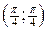 - точка перегиба.
График - точка перегиба.
График 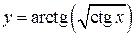 имеет вид имеет вид
| ||||||||||||||||||||||||||||||||||||||||
| ПП16.I №12 | Постройте график функции  .
Область определения функции: .
Область определения функции:  , это точка бесконечного разрыва функции, , это точка бесконечного разрыва функции,  для всех для всех 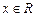 ; ;  при при  ; ;

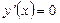 при при 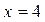 . .
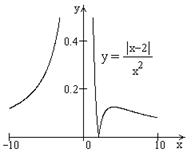 Построим схему. Построим схему.
|
| ПП16.I №13 | Найдите область определения функции (ООФ)  .
РЕШЕНИЕ:
ООФ .
РЕШЕНИЕ:
ООФ 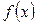 определяется системой неравенств: определяется системой неравенств:  Введем переменную
Введем переменную 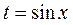 , тогда , тогда 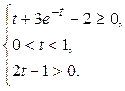 Из двух последних неравенств следует, что
Из двух последних неравенств следует, что 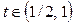 . Для решения первого неравенства рассмотрим функцию . Для решения первого неравенства рассмотрим функцию 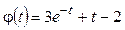 . Вычислим . Вычислим 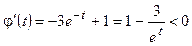 при при 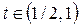 .
Итак, функция .
Итак, функция  убывает на этом интервале, и ее значения при этом остаются положительными, так как убывает на этом интервале, и ее значения при этом остаются положительными, так как 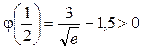 и и 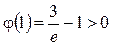 .
Область определения функции найдем из неравенства .
Область определения функции найдем из неравенства  , которому удовлетворяют , которому удовлетворяют 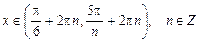 . .
| |
| ПП16.I №14 | 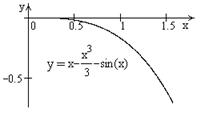 Докажите, что Докажите, что  для для 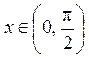 .
РЕШЕНИЕ:
Рассмотрим функцию .
РЕШЕНИЕ:
Рассмотрим функцию  , ,  . Производная . Производная  , так как , так как 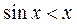 при при 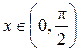 , т.е. функция , т.е. функция  является убывающей и не превосходит является убывающей и не превосходит 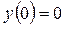 для для 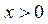 , т.е. , т.е.  , откуда , откуда 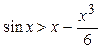 . .
| |
| ПП16.I №15 | Найдите интервал, в котором находятся корни многочлена 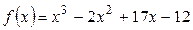 . .
 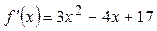 .
РЕШЕНИЕ:
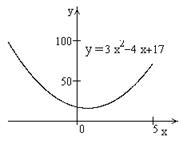
Полученный квадратный трехчлен имеет положительный коэффициент у старшего члена (на графике ветви параболы направлены вверх) и отрицательный дискриминант (график не имеет точек пересечения с осью .
РЕШЕНИЕ:
Полученный квадратный трехчлен имеет положительный коэффициент у старшего члена (на графике ветви параболы направлены вверх) и отрицательный дискриминант (график не имеет точек пересечения с осью  ), значит, все значения квадратного трехчлена лежат выше оси ), значит, все значения квадратного трехчлена лежат выше оси 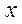 и и  при любых при любых  . .
 Из этого следует, что Из этого следует, что 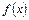 возрастает и имеет не более одного корня. Заметим, что возрастает и имеет не более одного корня. Заметим, что  , а , а 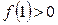 , т.е. корень многочлена , т.е. корень многочлена 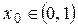 . Отметим, что корнем будет иррациональное число, так как на интервале . Отметим, что корнем будет иррациональное число, так как на интервале  не содержится целых чисел, которые были бы делителем свободного члена 12 исходного многочлена. не содержится целых чисел, которые были бы делителем свободного члена 12 исходного многочлена.
| |
| ПП16.I №16 | При каких значениях 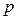 уравнение уравнение 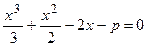 имеет ровно два различных корня?
РЕШЕНИЕ:
Рассмотрим функции имеет ровно два различных корня?
РЕШЕНИЕ:
Рассмотрим функции 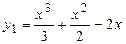 и и  . Абсциссы точек пересечения графиков этих функций будут решениями исходного уравнения. . Абсциссы точек пересечения графиков этих функций будут решениями исходного уравнения.
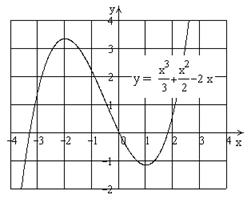 Исследуем поведение Исследуем поведение 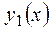 : : 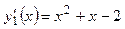 , найдем критические точки из уравнения , найдем критические точки из уравнения 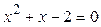  ; значения функции в этих точках равны ; значения функции в этих точках равны 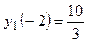 , , 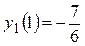 ; ;  – точка максимума, – точка максимума, 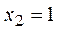 – точка минимума. Из анализа графика функции – точка минимума. Из анализа графика функции 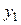 и возможных точек пересечения с и возможных точек пересечения с  видим, что исходное уравнение имеет два корня, если видим, что исходное уравнение имеет два корня, если  или или 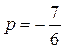 . .
| |
| ПП16.I №17 | Для каждого действительного числа  определите, сколько корней имеет многочлен определите, сколько корней имеет многочлен 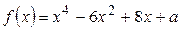 .
РЕШЕНИЕ: .
РЕШЕНИЕ:
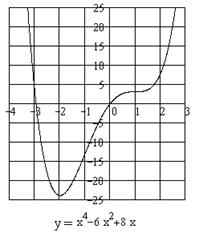 Вычислим Вычислим 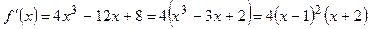 . Критическими точками производной являются значения . Критическими точками производной являются значения  и и 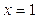 . Вычисление производной позволяет заключить, что . Вычисление производной позволяет заключить, что 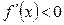 для для 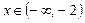 и и 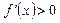 для для 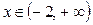 , и сделать вывод, что в точке , и сделать вывод, что в точке 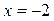 функция функция 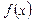 принимает минимальное значение принимает минимальное значение  . Таким образом, для всех . Таким образом, для всех  .
При .
При  и многочлен имеет один корень; при и многочлен имеет один корень; при  график многочлена не имеет общих точек с осью график многочлена не имеет общих точек с осью 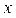 и, соответственно, корней; при и, соответственно, корней; при 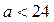 – два корня. – два корня.
| |
| ПП16.I №18 | Найдите число корней уравнения 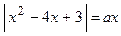 в зависимости от параметра в зависимости от параметра 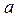 .
РЕШЕНИЕ: .
РЕШЕНИЕ:
 График функции График функции  пересекается с графиком пересекается с графиком 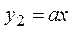 в различном количестве точек в зависимости от в различном количестве точек в зависимости от  . Области существования одного, двух, трех и четырех корней определяются геометрическим положением оси . Области существования одного, двух, трех и четырех корней определяются геометрическим положением оси 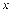 и касательными к графику функции в точках и касательными к графику функции в точках 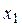 и и 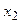 .
Найдем угловые коэффициенты этих касательных. Касательная .
Найдем угловые коэффициенты этих касательных. Касательная  задана уравнением задана уравнением 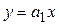 , , 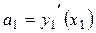 , где , где  . Координаты точки касания . Координаты точки касания 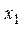 находим из условия: находим из условия:
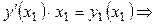 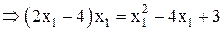 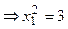 , ,  и и 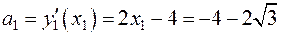 .
Аналогично для касательной .
Аналогично для касательной 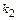 : : 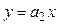 , , 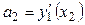 , где , где 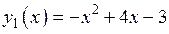 , ,
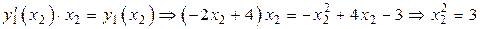 , , 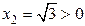 и и 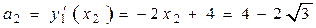 .
В итоге получаем, что при .
В итоге получаем, что при  уравнение имеет один корень; при уравнение имеет один корень; при 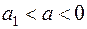 – корней нет; при – корней нет; при  и и 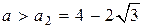 – два корня; при – два корня; при 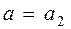 – три, а при – три, а при 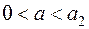 – четыре корня. – четыре корня.
| |
| ПП16.I №19 | Найдите наибольшее и наименьшее значения функции  на на 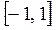 .
РЕШЕНИЕ:
Из условия .
РЕШЕНИЕ:
Из условия  найдем значения найдем значения 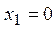 и и 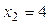 , в которых изменяется знак выражения, стоящего под знаком модуля. Функция не определена в точке , в которых изменяется знак выражения, стоящего под знаком модуля. Функция не определена в точке 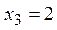 . Заметим, что . Заметим, что 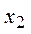 и и 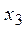 не принадлежат отрезку не принадлежат отрезку 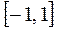 . .
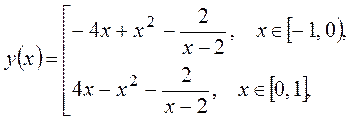 тогда
тогда 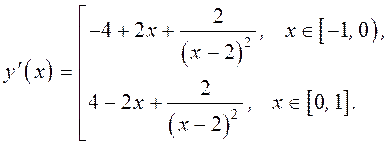 Критические точки находим из условия
Критические точки находим из условия  на каждом из интервалов: на каждом из интервалов:  Отрезку
Отрезку 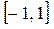 принадлежит одна критическая точка принадлежит одна критическая точка 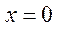 , в которой производная не существует. Вычислим значения функции , в которой производная не существует. Вычислим значения функции 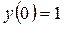 , ,  , ,  , , 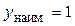 , , 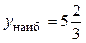 для для  . .
| |
| ПП16.I №20 | Для каждого значения параметра 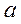 найдите наименьшее значение функции найдите наименьшее значение функции  на отрезке на отрезке  .
РЕШЕНИЕ: .
РЕШЕНИЕ:
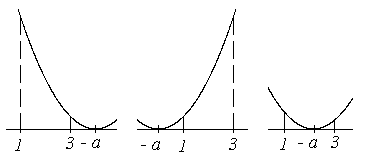 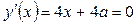 , точка , точка 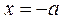 является точкой локального минимума функции. Наименьшее значение функции достигается в этой точке, если значение является точкой локального минимума функции. Наименьшее значение функции достигается в этой точке, если значение 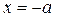 принадлежит интервалу принадлежит интервалу 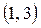 , и реализуется случай , и реализуется случай
 если если 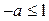 , то , то 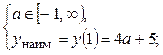 если если 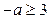 , то , то 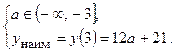
| |
| ПП16.I №21 | При каких значениях  функция функция 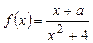 на на  принимает свои наибольшее и наименьшее значения на концах отрезка?
РЕШЕНИЕ:
Производная принимает свои наибольшее и наименьшее значения на концах отрезка?
РЕШЕНИЕ:
Производная 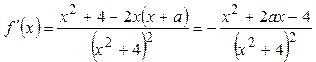 обращается в ноль при
обращается в ноль при 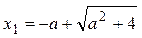 и и 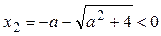 , , 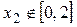 . В точке . В точке 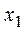 функция имеет максимум, значение функция имеет максимум, значение 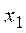 может принадлежать отрезку может принадлежать отрезку  при при 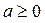 ; для того чтобы наибольшее и наименьшее значения достигались на концах отрезка, нужно, чтобы ; для того чтобы наибольшее и наименьшее значения достигались на концах отрезка, нужно, чтобы 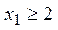 , т.е. , т.е.  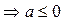 при условии, что при условии, что 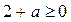 , т.е. , т.е. 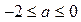 . .
| |
| ПП16.I №22 | Найдите число, куб которого превышает утроенный его квадрат на минимальное значение.
РЕШЕНИЕ:
Обозначим через 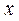 искомое число, составим функцию искомое число, составим функцию 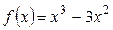 и найдем значение и найдем значение  , при котором , при котором 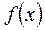 принимает минимальное значение.
Производная принимает минимальное значение.
Производная 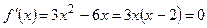 при при 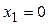 и и 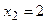 . При . При  , т.е. не удовлетворяется условие , т.е. не удовлетворяется условие  . Производная . Производная 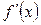 меняет знак при переходе через точку меняет знак при переходе через точку  : :  при при 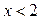 , , 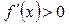 при при 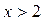 , т.е. в точке , т.е. в точке  функция функция  имеет минимум. Значит, искомое число равно двум. имеет минимум. Значит, искомое число равно двум.
| |
| ПП16.I №23 | В арифметической прогрессии шестой член равен 3, а разность прогрессии больше 0,5. При каком значении разности этой прогрессии произведение первого, четвертого и пятого ее членов является наибольшим?
РЕШЕНИЕ:
По условию  . Введем функцию . Введем функцию 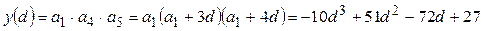 .
Найдем значение .
Найдем значение 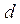 , при котором , при котором 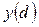 достигает наибольшего значения. Производная достигает наибольшего значения. Производная | |
|
|
|
|
|
|
Дата добавления: 2016-10-06; Мы поможем в написании ваших работ!; просмотров: 532 | Нарушение авторских прав
Поиск на сайте:
Лучшие изречения:








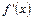
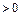
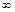




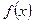 возрастает при
возрастает при  ; убывает при
; убывает при 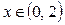 ;
; 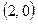 – точка минимума.
– точка минимума.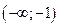
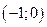
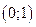
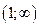
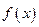

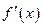
 .
.
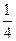
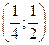






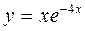 .
.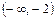
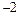
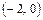
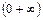

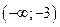
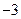
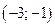
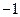





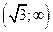

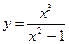 имеет вид:
имеет вид: