ПП 16.
I. ИССЛЕДОВАНИЕ ФУНКЦИЙ и построение графиков
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ
Графики элементарных функций
 1. Линейная функция:
1. Линейная функция:  .
.

2. Квадратичная функция:
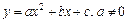 .
.

3. Степенные функции
3.1.  .
.
3.2.  ,
,  .
.

3.3. Иррациональные  .
.
 Трансцендентные функции
Трансцендентные функции
4. Показательная  .
.
5. Логарифмическая 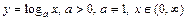 .
.
 6. Тригонометрические функции
6. Тригонометрические функции
6.1. 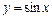 .
.
6.2.  .
.
6.3.  .
.
6.4. 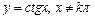 .
.
 7. Обратные тригонометрические функции
7. Обратные тригонометрические функции
7.1.  .
.  .
.
7.2.  .
.  .
.
7.3.  ,
,  .
.
7.4.  .
.  .
.
 ,
,  ,
,  .
.
8. Гиперболические функции
8.1. Гиперболический синус

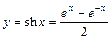 .
.
8.2. Гиперболический косинус
 .
.
8.3. Гиперболический тангенс
 .
.
8.4. Гиперболический котангенс
 .
.  ,
,  ,
,  ,
,  .
.
Асимптоты
1) 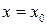 - вертикальная асимптота
- вертикальная асимптота  , если
, если  .
.
2)  - правая (левая) горизонтальная асимптота
- правая (левая) горизонтальная асимптота  , если
, если  .
.
3) 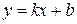 ,
,  ,
,  - наклонная асимптота
- наклонная асимптота  при
при 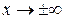 .
.
ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
Интервалы монотонности
Функция  , дифференцируемая на отрезке
, дифференцируемая на отрезке  , возрастает (убывает) тогда и только тогда, когда
, возрастает (убывает) тогда и только тогда, когда  (
( ),
),  .
.
Правило отыскания экстремумов функции
 Чтобы найти точки максимума и минимума функции
Чтобы найти точки максимума и минимума функции  , надо:
, надо:
1). Найти производную  , приравнять ее к нулю и решить полученное уравнение
, приравнять ее к нулю и решить полученное уравнение 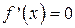 .
.
2). Найти точки, в которых производная  не существует.
не существует.
3). Исследовать знак производной  слева и справа от каждой критической точки.
слева и справа от каждой критической точки.

| 
| 
| Экстремум |
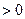
| 
| 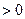
| нет |
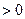
| 
| 
| max |

| 
| 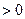
| min |

| 
| 
| нет |
С помощью второй производной:

| 
| Экстремум |

| max | |
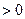
| min | |
Точки перегиба
Функция 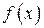 , дифференцируемая на отрезке
, дифференцируемая на отрезке  , выпукла вниз (вверх) тогда и только тогда, когда
, выпукла вниз (вверх) тогда и только тогда, когда  (
(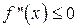 ),
),  .
.

| 
| 
| 
| 
| Перегиб |
| вып. вниз | 
| 
| вып. вниз | нет |
| вып. вниз | 
| 
| вып. вверх | есть |

| вып. вверх | 
| 
| вып. вниз | есть |

| вып. вверх | 
| 
| вып. вверх | нет |
Общая схема исследования функции и построения графика
1. Найти область определения функции; найти область значений функции; найти точки пересечения графика с осями координат, указать интервалы знакопостоянства функции.
2. Проверить функцию на периодичность; проверить функцию на четность и нечетность.
3. Исследовать функцию на непрерывность, найти точки разрыва функции и ее односторонние пределы в этих точках; определить наличие горизонтальных, вертикальных и наклонных асимптот.
4. Вычислив первую производную, найти критические точки и интервалы монотонности функции, выделить точки локальных экстремумов.
5. Вычислив вторую производную, найти интервалы выпуклости и точки перегиба графика функции.
6. Построить график.
Типы задач
Возрастание и убывание функций
 Функция
Функция 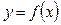 , дифференцируемая на интервале
, дифференцируемая на интервале  , возрастает (убывает) на
, возрастает (убывает) на  тогда и только тогда, когда
тогда и только тогда, когда 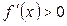 (
( ) для всех
) для всех  .
.
Геометрически это означает, что угол наклона касательной к графику возрастающей (убывающей) дифференцируемой функции острый (тупой), а угловые коэффициенты касательных соответственно положительны или отрицательны.
| № п/п | Примеры ПП 16 1. Возрастание и убывание функций |
| №1. |  По данному графику функции По данному графику функции  постройте вид графиков постройте вид графиков  .
Решение:
1) На интервале .
Решение:
1) На интервале   убывает, убывает,  , ,  . .
 2) На интервале 2) На интервале   возрастает, возрастает, 
 .
3) На интервале .
3) На интервале   убывает, убывает,  .
4) .
4) 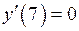 .
5) На интервале .
5) На интервале   возрастает, возрастает,  , на интервале , на интервале   убывает, убывает,  . Эти соображения позволяют построить примерный график . Эти соображения позволяют построить примерный график  .
6) .
6) 
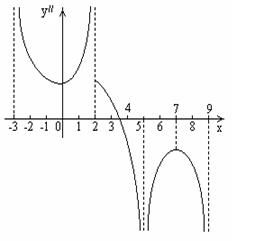 Та же последовательность действий, примененная к графику функции Та же последовательность действий, примененная к графику функции  , дает примерный график второй производной , дает примерный график второй производной  . .
|
| №2. | 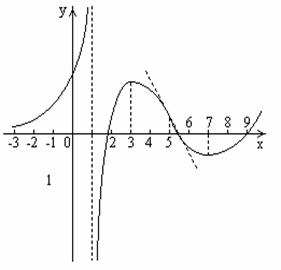 По данному графику производной По данному графику производной  постройте вид графика функции постройте вид графика функции  .
Решение:
1) На интервале .
Решение:
1) На интервале   , ,  возрастает, возрастает,  , т.е., скорость возрастания , т.е., скорость возрастания  также неограниченно возрастает, а следовательно, и сама функция также неограниченно возрастает, а следовательно, и сама функция  неограниченно возрастает, т.о., неограниченно возрастает, т.о.,  – вертикальная асимптота графика.
2) На интервале – вертикальная асимптота графика.
2) На интервале   , ,  возрастает, причем возрастает, причем  , (чем ближе точка к , (чем ближе точка к  – справа от нее, тем больше скорость возрастания), что указывает, что – справа от нее, тем больше скорость возрастания), что указывает, что  , т.е., , т.е.,  – точка разрыва второго рода.
3) В точке – точка разрыва второго рода.
3) В точке  производная меняет знак с «+» на «–», производная меняет знак с «+» на «–»,  – точка локального максимума.
4) На интервале – точка локального максимума.
4) На интервале   , ,  убывает.
5) В точке убывает.
5) В точке  производная меняет знак с «–» на «+», производная меняет знак с «–» на «+»,  – точка локального минимума. – точка локального минимума.
 6) При 6) При  функция возрастает.
Эти соображения позволяют построить примерный график функция возрастает.
Эти соображения позволяют построить примерный график  : :
|
| №3. | Функция  возрастает в своей области определения, так как возрастает в своей области определения, так как  при любых при любых  . .
|
| №4. | Функция  возрастает на интервале возрастает на интервале 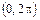 , так как для , так как для   .
Полезный вывод: поскольку .
Полезный вывод: поскольку  , то , то  , значит , значит  для для  . .
|
Экстремумы функции
Необходимым условием существования экстремума функции является равенство нулю ее производной в точке экстремума: 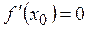 (если в этой точке производная существует).
(если в этой точке производная существует).
Геометрически это означает, что касательная к графику функции 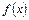 в точке экстремума параллельна оси
в точке экстремума параллельна оси 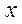 .
.
Достаточным условием существования экстремума функции в точке  является изменение знака ее первой производной в этой точке:
является изменение знака ее первой производной в этой точке:
в точке  максимума функции знак производной изменяется с положительного на отрицательный, что соответствует возрастанию функции до точки максимума при
максимума функции знак производной изменяется с положительного на отрицательный, что соответствует возрастанию функции до точки максимума при  и убыванию после нее при
и убыванию после нее при  .
.
Существуют точки, в которых необходимое условие экстремума не выполняется, но тем не менее функция в них может иметь экстремум.
Критическими называются точки, в которых производная функции равняется нулю, не существует или обращается в бесконечность. Критические точки разбивают область определения функции на интервалы монотонности.
| № п/п | Примеры ПП 16 2. Экстремумы функции |
| №5. | Для функции  на отрезке на отрезке  значение значение  является минимальным, т.к. производная является минимальным, т.к. производная  равна нулю в точке равна нулю в точке  . .
|
| №6. |  Функция Функция  не дифференцируема в точке не дифференцируема в точке  , так как касательные к графику функции слева и справа от точки , так как касательные к графику функции слева и справа от точки  различны, однако функция имеет минимум в этой точке. Функция различны, однако функция имеет минимум в этой точке. Функция 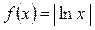 является строго убывающей при является строго убывающей при  и строго возрастающей при и строго возрастающей при 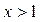 . В точке . В точке 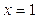 график имеет острый минимум (так называемую угловую точку). график имеет острый минимум (так называемую угловую точку).
|
| №7 |  Функция Функция  и ее производная имеют бесконечный разрыв при и ее производная имеют бесконечный разрыв при  . Функция возрастает при . Функция возрастает при  и убывает при и убывает при  , но экстремума в точке , но экстремума в точке  не имеет. не имеет.
|
| №8. |  Функция Функция  не дифференцируема в точке не дифференцируема в точке  , так как , так как  при при  , график функции имеет в точке 0 вертикальную касательную, функция является убывающей при , график функции имеет в точке 0 вертикальную касательную, функция является убывающей при 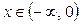 , возрастающей при , возрастающей при  , в точке , в точке  функция имеет минимум (такая точка графика называется точкой возврата). функция имеет минимум (такая точка графика называется точкой возврата).
|
| №9. |  Для функции Для функции 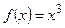 в точке в точке  выполняется необходимое условие экстремума выполняется необходимое условие экстремума  . Однако точка . Однако точка  не является точкой экстремума этой функции, в ней не выполняется достаточное условие экстремума, т.к. не является точкой экстремума этой функции, в ней не выполняется достаточное условие экстремума, т.к.  для любых для любых  и функция и функция  возрастает на всей числовой оси. возрастает на всей числовой оси.
|
| №10 |  Для функции Для функции  в точке в точке  производная не существует, однако экстремум отсутствует. производная не существует, однако экстремум отсутствует.
|
Асимптоты графика функции
| № п/п | Примеры ПП 16 3. Асимптоты графика функции |
| №11. | У графика   существует левая горизонтальная асимптота существует левая горизонтальная асимптота  ( ( ) и не существует правой горизонтальной асимптоты. ) и не существует правой горизонтальной асимптоты.
|
| №12 | У графика   существует правая горизонтальная асимптота существует правая горизонтальная асимптота  ( ( ) и не существует левой горизонтальной асимптоты. ) и не существует левой горизонтальной асимптоты.
|
| №13 | У графика   существуют обе горизонтальные асимптоты: существуют обе горизонтальные асимптоты:  - левая горизонтальная асимптота ( - левая горизонтальная асимптота ( ), ),
 - правая горизонтальная асимптота ( - правая горизонтальная асимптота ( ). ).
|
| №14 |  У графика У графика 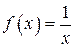 обе горизонтальных асимптоты обе горизонтальных асимптоты  существуют и совпадают ( существуют и совпадают ( ). Кроме того, график функции ). Кроме того, график функции  имеет вертикальную асимптоту имеет вертикальную асимптоту  , поскольку , поскольку  , ,  . .
|
| №15 | 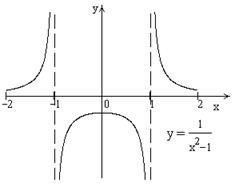 Кривая Кривая  имеет вертикальные асимптоты имеет вертикальные асимптоты  и и  . .
|
| №16 |  Построим график функции Построим график функции  без использования производной.
Преобразуем выражение: без использования производной.
Преобразуем выражение:  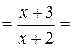  , , 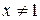 .
График этой функции получается смещением графика .
График этой функции получается смещением графика  на две единицы влево, на одну единицу вверх и выкалыванием точки графика с абсциссой на две единицы влево, на одну единицу вверх и выкалыванием точки графика с абсциссой  .
Прямые .
Прямые  и и  являются вертикальной и горизонтальной асимптотами.
Для гиперболы с центром симметрии в точке являются вертикальной и горизонтальной асимптотами.
Для гиперболы с центром симметрии в точке   уравнения вертикальной и горизонтальной асимптот имеют вид: уравнения вертикальной и горизонтальной асимптот имеют вид:  и и  . .
|
| №17 | Исследуйте поведение функции  в точке в точке  . .
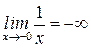 , ,  , ,
 , ,  .
Прямая .
Прямая  является вертикальной асимптотой. является вертикальной асимптотой.
|
| №18 | Найдите асимптоты графика функции  . .  , , 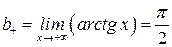 , ,  .
График имеет две несовпадающие наклонные асимптоты: левую .
График имеет две несовпадающие наклонные асимптоты: левую  и правую и правую  . . 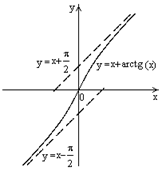
|






