Свойства проекции вектора
1) проекция суммы векторов какую либо ось = сумме проекций слагаемых векторов на эту ось.
2) алгебраическая проекция вектора на какую либо ось = произведению блины вектора на cos угла между вектором и положит. Напр. Отрезком оси.
14. Коллинеарные векторы это векторы, лежащие на параллельных прямых (или на одной и той же прямой).
Теорема о разложении вектора.
Пусть a и b - два неколлинеарных вектора плоскости. Тогда для любого вектора m плоскости существует, и притом единственная, пара чисел x и y такая, что m= x a+ y b.
15. Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.
Для компланарности трех векторов a, b и c трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Теорема. Любой вектор m может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых некомпланарных векторов а, b и с:
m = x a + y b + z c
16. Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.
Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
Декартовым базисом трехмерного пространства называется любые три неколлинеарных вектора, взятые в определенном порядке.
ДЕКАРТОВА СИСТЕМА КООРДИНАТ, система, введенная Рене ДЕКАРТОМ, в которой положение точки определяется расстоянием от нее до взаимно пересекающихся линий (осей). В простейшем варианте системы оси (которые обозначаются как х и у) перпендикулярны. Положение точки задается парой чисел (х, у). Абсцисса, х, -это расстояние от точки до оси у, измеренное в направлении оси х; ордината, у, -это расстояние до оси х.
Если векторы e1, e2 и e3, составляющие базис, — попарно перпендикулярные единичные векторы, то система координат О, e1, e2, e3 называется прямоугольной декартовой системой координат в пространстве.
Определения смешанного произведения, его геометрический смысл
Рассмотрим произведение векторов а, b и с, составленное следующим образом: (ахb)•с. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторноскалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.
Выясним геометрический смысл выражения (ахb)*с. Построим параллелепипед, ребрами которого являются векторы а, b, с и вектор d =ахb (см. рис. 22).
Имеем: (а х b) • с = d • с = |d| • прdс, |d|=|  а х b| =S, где S — площадь параллелограмма, построенного на векторах а и b, прdс = Н Для правой тройки векторов и прdс = - Н для левой, где Н— высота параллелепипеда. Получаем: (axb)*c =S *(±H), т. е. (axb)*c =±V, где V — объем параллелепипеда, образованного векторами а, b и с.
а х b| =S, где S — площадь параллелограмма, построенного на векторах а и b, прdс = Н Для правой тройки векторов и прdс = - Н для левой, где Н— высота параллелепипеда. Получаем: (axb)*c =S *(±H), т. е. (axb)*c =±V, где V — объем параллелепипеда, образованного векторами а, b и с.
Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.
28. Компланарные векторы
Определение.
Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.
Два вектора  и
и  трехмерного пространства всегда компланарны. Это утверждение легко доказать. Пусть a и b – прямые, на которых лежат векторы
трехмерного пространства всегда компланарны. Это утверждение легко доказать. Пусть a и b – прямые, на которых лежат векторы  и
и  соответственно. Проведем через начало вектора
соответственно. Проведем через начало вектора  прямую b1, параллельную прямой b, а через начало вектора
прямую b1, параллельную прямой b, а через начало вектора  прямую a1, праллельную прямой a. Плоскости, образуемые прямыми a и b1, а так же прямыми b и a1, параллельны по построению, а векторы
прямую a1, праллельную прямой a. Плоскости, образуемые прямыми a и b1, а так же прямыми b и a1, параллельны по построению, а векторы  и
и  принадлежат им. Следовательно, векторы
принадлежат им. Следовательно, векторы  и
и  компланарны.А как же определить, являются ли три вектора компланарными?Для этого существует необходимое и достаточное условие компланарности трех векторов в пространстве. Оно основано на понятии смешанного произведения векторов. Сформулируем его в виде теоремы.
компланарны.А как же определить, являются ли три вектора компланарными?Для этого существует необходимое и достаточное условие компланарности трех векторов в пространстве. Оно основано на понятии смешанного произведения векторов. Сформулируем его в виде теоремы.
Теорема.
Для компланарности трех векторов 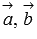 и
и  трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Доказательство.
Пусть  , докажем что векторы
, докажем что векторы 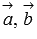 и
и  компланарны.Так как
компланарны.Так как  , то векторы
, то векторы  и
и  перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор
перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор  перпендикулярен и вектору
перпендикулярен и вектору  и вектору
и вектору  . Следовательно, векторы
. Следовательно, векторы 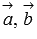 и
и  компланарны, так как перпендикулярны одному вектору
компланарны, так как перпендикулярны одному вектору  .Пусть теперь векторы
.Пусть теперь векторы 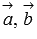 и
и  компланарны, докажем равенство нулю смешанного произведения
компланарны, докажем равенство нулю смешанного произведения  .Так как векторы
.Так как векторы 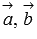 и
и  компланарны, то вектор
компланарны, то вектор  перпендикулярен каждому из них, следовательно, скалярное произведение вектора
перпендикулярен каждому из них, следовательно, скалярное произведение вектора  на
на  равно нулю, что означает равенство нулю смешанного произведения
равно нулю, что означает равенство нулю смешанного произведения  .
.
Итак, теорема полностью доказана.






