Генерирующее соотношение показывает с каким из эффектов смешанный данный эффект. Пример:х1*х2=х3 (1) – эффект 3 смешан с эффектами 1 и 2. Умножим (1) на х3, тогда х1*х2*х3=1 (т.к.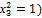 
. Символическое обозначение произведения столбцов равное (+1) или (-1) называют определяющим контрастом. С помощью него можно определить систему смешивания эффектов. Чтобы определить какой эффект смешан с данным, нужно умножить обе части определяющего контраст на столбец, соответствующий данному эффекту: х1*х2* 
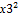=х3, х3=х1*х2.
Способ расчета коэффициентов регрессии при использовании полного и дробного факторного эксперимента.
Рассчитывают по формуле: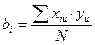 
. Для подсчета коэффициентов регрессии нужно столбцу у приписать знаки столбца хi, сложить значения параметра оптимизации со своими знаками и поделить на число опытов. В0 можно также подсчитать. В том случае, если при справедливости уравнения 
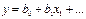, то оно верно и для средне-арифметических значений: 
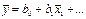. Но 
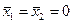, поэтому 
.
При использовании ПФЭ и ДФЭ все дисперсии коэффициентов регрессии равны между собой.
Линейная модель уравнения регрессии в матричной форме.
Линейная модель: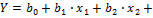 
… 
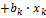
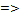X 
B=Y где Х – матрица условий эксперимента. В – матрица неизвестных коэффициентов регрессии. Y – матрица результатов наблюдений (параметров оптимизации). N – опыты.
Х=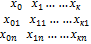 
B= 
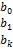Y=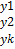 
Указать какая часть поверхности отклика называется почти стационарной.
Часть поверхности отклика вблизи экстремума называется почти стационарной областью, она обычно описывается при помощи нелинейных уравнений, чаще всего это полином второго порядка: 
… 
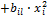, где к- число факторов.
Объяснить, каким образом матрицу центрального композиционного планирования можно сделать ротатабельной.
Инвариантность к вращению координат, позволяющая предсказать значение параметра оптимизации в различных точках факторного пространства с минимальным и на равном расстоянии от центра эксперимента дисперсии. Из этого условия величина звездного плеча определяется из условия: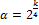 
(для ПФЭ). Если ядро- дробные реплики, то: 
.
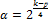При ротатабельном планировании 2го порядка важно количество параллельных опытов в центре плана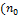 
)
Т.к.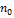 
определяет характер распределения. 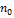должно обеспечивать униформу планирования, которая дает равномерное и постоянное распределение информации на разных расстояниях от центра. в общем случае число опытов в центре эксперимента выбирают так, чтобы некоторое постоянное 
.
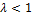Основные особенности этапа выбора факторов.
Указать, каким образом матрицу центрального композиционного планирования можно сделать ортогональной.
Планы ортогональны, если: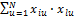 
= 
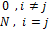где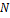 
-общее число факторов, 
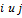– число факторов, 
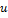- номер опыта. Это условие для матрицы ЦКП не выполняется, т.к. 
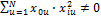и 
т.к.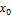 
везде ±1, 
.
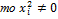Можно добиться полной ортогональности, если преобразовать квадратичные переменные и специальным образом выбрать звездное плечо. Для этого вместо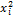 
вводят новую переменную:
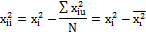
В результате этого выполняется условие ортогональности:
= 
= 
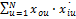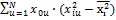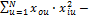
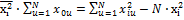=0
Если планирование для двух факторов, то: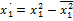 
;: 
(
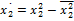
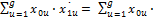)=0
