Рассчитывают по формуле: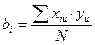 
. Для подсчета коэффициентов регрессии нужно столбцу у приписать знаки столбца хi, сложить значения параметра оптимизации со своими знаками и поделить на число опытов. В0 можно также подсчитать. В том случае, если при справедливости уравнения 
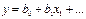, то оно верно и для средне-арифметических значений: 
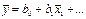. Но 
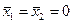, поэтому 
.
При использовании ПФЭ и ДФЭ все дисперсии коэффициентов регрессии равны между собой.
Способ определения доверительных интервалов коэффициентов регрессии.
, 
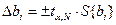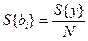
t – критерий Стьюдента (из таблиц)
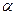- уровень значимости
N – число опытов в матрице планирования
S{bi} – СКО в определении коэффициентов регрессии, S{у} – дисперсия опыта
Статистически значимые и статистически незначимые коэффициенты регрессии.
После проведения эксперимента рассчитывают коэф регрессии и определяют их значимость. Для этого рассчитывают дисперсии в определении коэф регрессии. Коэффициент регрессии статистически значим, если его абсолютная величина больше либо равна доверительному интервалу 
или 
. Если коэффициенты статистически не значимы, то их убирают из уравнения.
Схема расчета дисперсии неадекватности.
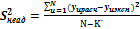где 
- значение параметров оптимизации.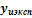 
- значение параметра в некотором опыте u,рассчитанное при помощи математической модели. 
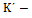число число коэффициентов в уравнении, включая 
. 
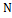- число опытов в матрице планирования. 
= 
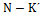- число степеней свободы, при определении дисперсии неадекватности.
Если опыты дублируются равномерно, например в каждом опыте по n раз, то рассчитываем так: 
.
Критерий Фишера представляет собой отношение дисперсии предсказания полученной модели к дисперсии опыта. Он показывает во сколько раз модель предсказывает хуже чем опыт. Гипотеза об адекватности модели принимается тогда, когда расчетное значение критерия Фишера, не превышает табличного значения для выбранного уровня значимости.
Способ проверки адекватности линейного уравнения с помощью критерия Стьюдента.
Адекватность линейного уравнения определяют по критерию Стьюдента, рассчитанного по формуле: 
.
Затем расчетную величину критерия Стьюдента сравнивают с его табличным значением. Если выполняется неравенство: 
, то линейная модель уравнения считается адекватной.
Общая схема планирования экспериментов для решения экстремальных задач.
Экстремальная задача предполагает, что параметр оптимизации связан с факторами тем или иным математическим выражением. Требуется так поставить эксперименты, чтобы при их минимальном количестве, варьируя значения независимых переменных найти область оптимальных значений параметров, и следовательно построить математическую модель:
1.выбрать параметры оптимизации у и влияющие факторы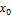 
, 
, 
… 
.
2.выбрать основной уровень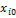 
и интервалы варьирования Δ 
влияющих факторов.
3.выбрать план эксперимента (полный или дробный факторный эксперимент).
4.провести эксперименты.
5.на их основе составить модель (линейную, квадратичную).
6.методом крутого восхождения найти оптимум.
