Цель: Сформировать умения разрабатывать алгоритмы и программы с использованием алгоритмов на графах
Программное обеспечение: TURBO PASCAL 7.1
Оснащение: персональный компьютер, практикум
Время проведения: 2 уч. часа
Литература:
Павловская Т.А. Паскаль. Программирование на языке высокого уровня. Учебник для вузов. СПб.: Питер, 2008.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
1. Сформулируйте определение размещения.
2. Сформулируйте определение сочетания.
3. Приведите примеры комбинаторных алгоритмов.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Граф – это нелинейная многосвязная динамическая структура, отображающая свойства и связи сложного объекта.
Многосвязная структура обладает следующими свойствами:
- на каждый элемент (узел, вершину) может быть произвольное количество ссылок;
- каждый элемент может иметь связь с любым количеством других элементов;
- каждая связка (ребро, дуга) может иметь направление и вес.
В узлах графа содержится информация об элементах объекта. Связи между узлами задаются ребрами графа. Ребра графа могут иметь направленность, показываемую стрелками, тогда они называются ориентированными, ребра без стрелок – неориентированными.
Граф, все связи которого ориентированные, называется ориентированным графом или орграфом; граф со всеми неориентированными связями – неориентированным графом; граф со связями обоих типов – смешанным графом. Неориентированные связи приведены на рисунке 18.1 а, а ориентированные – на рисунке 18.1 б.

Рисунок 18.1 ― Графы: а – неориентированный и б –ориентированный
Для ориентированного графа число ребер, входящих в узел, называется полустепенью захода узла, выходящих из узла – полустепенью исхода. Количество входящих и выходящих ребер может быть любым, в том числе и нулевым. Граф без ребер является нуль-графом.
Если ребрам графа соответствуют некоторые значения, то граф и ребра называются взвешенными. Мультиграфом называется граф, имеющий параллельные (соединяющие одни и те же вершины) ребра, в противном случае граф называется простым.
Путь в графе – это последовательность узлов, связанных ребрами. Элементарным называется путь, в котором все ребра различны. Простым называется путь, в котором все вершины различны. Путь от узла к самому себе называется циклом, а граф, содержащий такие пути, – циклическим.
Два узла графа смежны, если существует путь от одного из них до другого. Узел называется инцидентным к ребру, если он является его вершиной, т. е. ребро направлено к этому узлу.
Логически структура-граф может быть представлена матрицей смежности или матрицей инцидентности.
Матрицей смежности для n узлов называется квадратная матрица adj порядка n. Элемент матрицы a (i, j) равен 1, если узел j смежен с узлом i (есть путь < i, j >), и 0 – в противном случае (рис. 18.2).

Рисунок 18.2 ― Граф и его матрица смежности
Если граф неориентирован, то a (i, j) = a (j, i), т. е. матрица симметрична относительно главной диагонали.
Матрицы смежности используются при построении матриц путей, дающих представление о графе по длине пути: путь длиной в 1 – смежный участок, путь длиной 2 – (< A,B >,< B,C >),... в n смежных участков, где n – максимальная длина, равная числу узлов графа. На рисунке 18.3 даны путевые матрицы пути adj 2, adj 3, adj 4 для графа рисунке 18.2.

Рисунок 18.3 ― Матрицы путей
Матрицы инцидентности используются только для орграфов. В каждой строке содержится упорядоченная последовательность имен узлов, с которыми данный узел связан ориентированными (исходящими) ребрами. На рисунке 18.4 показана матрица инцидентности для графа на рисунке 18.2.

Рисунок 18.4 ― Матрицы инцидентности
Машинное представление оpгpафов
Существуют два основных метода представления графов в памяти ЭВМ: матричный, т.е. массивами, и связными нелинейными списками. Выбор метода представления зависит от природы данных и операций, выполняемых над ними. Если задача требует большого числа включений и исключений узлов, то целесообразно представлять граф связными списками, в противном случае можно применить и матричное представление.
Матричное представление орграфов
При использовании матриц смежности их элементы представляются в памяти ЭВМ элементами массива. При этом, для простого графа матрица состоит из нулей и единиц, для мультиграфа – из нулей и целых чисел, указывающих кратность соответствующих ребер, для взвешенного графа – из нулей и вещественных чисел, задающих вес каждого ребра.
Например, для простого ориентированного графа, изображенного на рисунке 18.2, массив определяется как:
mas:array[1..4,1..4]=((0,1,0,0),(0,0,1,1), (0,0,0,1),(1,0,1,0))Матрицы смежности применяются тогда, когда в графе много связей и матрица хорошо заполнена.
Связное представление орграфов
Орграф представляется связным нелинейным списком, если он часто изменяется или если полустепени захода и исхода его узлов велики. Рассмотрим два варианта представления орграфов связными нелинейными списковыми структурами.
В первом варианте два типа элементов – атомарный и узел связи. На рис. 5 показана схема такого представления для графа на рисунке 18.2. Скобочная запись связей этого графа:
(< A,B >,< B,C >,< C,D >,< B,D >,< D,C >)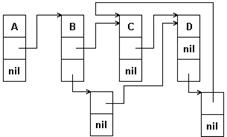
Рисунок 18.5 ― Машинное представление графа элементами двух типов
Более рационально представлять граф элементами одного формата, двойными: атом-указатель и указатель-указатель или тройными: указатель-data/down-указатель. На рисунке 18.6 тот же граф представлен элементами одного формата.

Рисунок 18.6 ― Машинное представление графа однотипными элементами
Многосвязная структура – граф – находит широкое применение при организации банков данных, управлении базами данных, в системах программного иммитационного моделирования сложных комплексов, в системах исскуственного интеллекта, в задачах планирования и в других сферах.
В качестве примера приведем программу, находящую кратчайший путь между двумя указанными вершинами связного конечного графа.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
{Алгоритм Дейкстры} Program Example_1; Const n=5; max=10000; Var a: Array [1..n,1..n] of Integer; v0,w,edges: Integer; from,tu,length: Array [1..n] of Integer; Procedure adjinit;{эта пpоцедуpа задает вес pебеp гpафа посpедством опpеделения его матpицы смежности A pазмеpом N x N } Var i,j: Integer; Begin {"обнуление" матpицы (веpшины не связаны)} For i:=1 to n do For j:=1 to n do a[i,j]:=max; For i:=1 to n do a[i,i]:=0;{задание длин pебеp, соединяющих смежные узлы гpафа} a[1,2]:=12; a[1,3]:=18; a[1,4]:=10; a[2,1]:=12; a[2,3]:=6; a[2,5]:=9; a[3,1]:=18; a[3,2]:=6; a[3,4]:=7; a[3,5]:=3; a[4,1]:=10; a[4,3]:=7; a[4,5]:=15; a[5,2]:=9; a[5,3]:=3; a[5,4]:=15; end;Procedure printmat;{эта пpоцедуpа выводит на экpан дисплея матpицу смежности A взвешенного гpафа} Var i,j: Integer; Begin writeln; writeln('Матpица смежности взвешенного гpафа (',n,'x',n,'):'); writeln; For i:=1 to n do Begin write ('Е'); For j:=1 to n do If a[i,j]=max Then write(' ----') Else write(a[i,j]:6); writeln(' Е') End; writeln; writeln (' ("----" - pебpо отсутствует)') end;Procedure dijkst;
СОДЕРЖАНИЕ РАБОТЫ: Написать программу с использованием алгоритма обхода графа в глубину.
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
1. Сформулируйте определение графа.
2. Перечислите виды графов.
3. Приведите примеры алгоритмов для работы с графами.
ДОМАШНЕЕ ЗАДАНИЕ
Выучить алгоритмы с применением графов.






