Цель: Сформировать умения разрабатывать рекурсивные алгоритмы и программы
Программное обеспечение: TURBO PASCAL 7.1
Оснащение: персональный компьютер, практикум
Время проведения: 2 уч. часа
Литература:
1. Немнюгин С., Перколаб Л. Изучаем Turbo Pascal. СПб.: Питер, 2008. С. 157-163, 273-278.
2. Немнюгин С.А. Turbo Pascal. Практикум. 2-е изд. СПб.: Питер, 2007. С. 217-220.
3. Павловская Т.А. Паскаль. Программирование на языке высокого уровня. Учебник для вузов. СПб.: Питер, 2008. С. 105-107.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
1. Приведите классификацию алгоритмов сортировки.
2. Объясните алгоритм сортировки «пузырька».
3. Объясните алгоритм сортировки вставка.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Рекурсия — это такой способ организации вспомогательного алгоритма (подпрограммы), при котором эта подпрограмма (процедура или функция) в ходе выполнения ее операторов обращается сама к себе. Вообще, рекурсивным называется любой объект, который частично определяется через себя.
Например, приведенное ниже определение двоичного кода является рекурсивным:
<двоичный код>::= <двоичная цифра> | <двоичный код><двоичная цифра>
<двоичная цифра>::= 0 | 1
Здесь для описания понятия были использованы, так называемые, металингвистические формулы Бэкуса-Наура (язык БНФ); знак "::=" обозначает "по определению есть", знак "|" — "или".
Вообще, в рекурсивном определении должно присуствовать ограничение, граничное условие, при выходе на которое дальнейшая инициация рекурсивных обращений прекращается.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Пример 1.
Классический пример, без которого не обходятся ни в одном рассказе о рекурсии, — определение факториала. С одной стороны, факториал определяется так:
n!=1*2*3*...* n. С другой стороны,
Граничным условием в данном случае является n <=1.
Пример 2.
Определим функцию K(n), которая возвращает количество цифр в заданном натуральном числе n:
Задание. По аналогии определите функцию S(n), вычисляющую сумму цифр заданного натурального числа.
Пример 3.
Функция C(m, n), где 0 <= m <= n, для вычисления биномиального коэффициента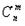 
по следующей формуле 
является рекурсивной.
Ниже будут приведены программные реализации всех этих примеров.
Обращение к рекурсивной подпрограмме ничем не отличается от вызова любой другой подпрограммы. При этом при каждом новом рекурсивном обращении в памяти создаётся новая копия подпрограммы со всеми локальными переменными. Такие копии будут порождаться до выхода на граничное условие. Очевидно, в случае отсутствия граничного условия, неограниченный рост числа таких копий приведёт к аварийному завершению программы за счёт переполнения стека.
Порождение все новых копий рекурсивной подпрограммы до выхода на граничное условие называется рекурсивным спуском. Максимальное количество копий рекурсивной подпрограммы, которое одновренно может находиться в памяти компьютера, называется глубиной рекурсии. Завершение работы рекурсивных подпрограмм, вплоть до самой первой, инициировавшей рекурсивные вызовы, называется рекурсивным подъёмом.
Выполнение действий в рекурсивной подпрограмме может быть организовано одним из вариантов:
Begin Begin Begin
P; операторы; операторы;
операторы; P P;
End; End; операторы
End;
рекурсивный подъём рекурсивный спуск и рекурсивный спуск, и рекурсивный подъём
Здесь P — рекурсивная подпрограмма. Как видно из рисунка, действия могут выполняться либо на одном из этапов рекурсивного обращения, либо на обоих сразу. Способ организации действий диктуется логикой разрабатываемого алгоритма.
Пример 4.
{ Функция }
Function Factorial(N:integer):Extended;
Begin
If N<=1 Then Factorial:=1 Else Factorial:=Factorial(N-1)*N
End;
{ Процедура }
Procedure Factorial(N:integer; Var F:Extended);
Begin
If N<=1 Then F:=1 Else Begin Factorial(N-1, F); F:=F*N End
End;
Пример 5.
{ Функция }
Function K(N:Longint):Byte;
Begin
If N<10 Then K:=1 Else K:=K(N div 10)+1 End;
{ Процедура }
Procedure K(N:Longint; Var Kol:Byte)
Begin
If N<10 Then Kol:=1 Else Begin K(N Div 10, Kol); Kol:=Kol+1 End; End;
Пример 6.
{ Функция }
function C(m, n:Byte):Longint;
Begin
If (m=0) or (m=n) Then C:=1 Else C:=C(m, n-1)+C(m-1, n-1)
End;
{ Процедура }
Procedure C(m, n: Byte; Var R: Longint);
Var R1, R2: Longint;
Begin
If (m=0) or (m=n) Then R:=1 Else Begin
C(m, n-1, R1);
C(m-1, n-1, R2);
R:=R1+R2
End;
End;
Пример 7. Вычислить сумму элементов линейного массива.
При решении задачи используем следующее соображение: сумма равна нулю, если количество элементов равно нулю, и сумме всех предыдущих элементов плюс последний, если количество элементов не равно нулю.
Program Rec2;
Type LinMas = Array[1..100] Of Integer;
Var A: LinMas;
I, N: Byte;
{ Рекурсивная функция }
Function Summa(N: Byte; A: LinMas): Integer;
Begin
If N = 0 Then Summa:= 0 Else Summa:= A[N] + Summa(N - 1, A)
End;
{ Основная программа }
Begin
Write('Количество элементов массива? '); ReadLn(N); Randomize;
For I:= 1 To N Do
Begin
A[I]:= -10 + Random(21); Write(A[I]: 4)
End;
WriteLn; WriteLn('Сумма: ', Summa(N, A))
End.
Использование рекурсии является красивым приёмом программирования. В то же время в большинстве практических задач этот приём неэффективен с точки зрения расходования таких ресурсов ЭВМ, как память и время исполнения программы. Использование рекурсии увеличивает время исполнения программы и зачастую требует значительного объёма памяти для хранения копий подпрограммы на рекурсивном спуске.
СОДЕРЖАНИЕ РАБОТЫ: Написать алгоритм и отладить программу с использованием рекурсивной функции.
| Вариант | Задание | Вариант | Задание |
| №1, 11 | 
| №6, 16 | 
|
| №2, 12 | 
| №7, 17 | 
|
| №3, 13 | 
| №8, 18 | 
|
| №4, 14 | 
| №9, 19 | 
|
| №5, 15 |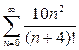 
| №10, 20 | 
|
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
1. Дайте понятие рекурсивной функции.
2. Дайте понятие рекурсивного алгоритма (подпрограммы).
3. Дайте понятие граничному условию и его назначению в рекурсивной подпрограмме.
4. Приведите пример рекурсивного спуска.
5. Приведите пример рекурсивного подъёма.
ДОМАШНЕЕ ЗАДАНИЕ
Выучить определение рекурсии; достоинства и недостатки рекурсивных программ; научиться разрабатывать рекурсивные процедуры и функции.
