Класів лишків за даним простим модулем
Вище як приклад скінченного поля розглядалося кільце 
класів лишків цілих чисел за модулем простого числа 
.
Арифметика над скінченними полями широко застосовується в криптографії і є основою багатьох криптосистем. Елементами таких полів є тільки скінченні числа, при операціях над якими відсутні похибки заокруглення.
Покажемо, як перенести структуру поля з на множину без алгебраїчної структури.
Для простого числа позначимо через 
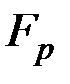множину 
. Визначимо відображення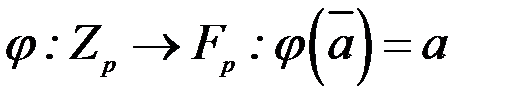 
, де 
(
– класи лишків за модулем ). Тоді множина 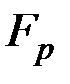із структурою поля, індукованою відображенням 
, також утворює скінченне поле, яке називається полем Галуа порядку за ім’ям їх першого дослідника Еваріста Галуа.Таке поле ще позначають 
(
– Galois Field – поле Галуа).
Відображення є ізоморфізмом,оскільки зберігає операції:
. Нулем скінченного поля буде нуль 0, а одиницею – одиниця 1і його структура співпадає із структурою поля .
При обчисленнях з елементами поля використовується арифметика цілих чисел із зведенням за модулем .
Приклад 3. Найпростішим і найважливішим у застосуваннях є поле 
другого порядку з елементами 
, для яких виконуються операції + і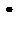 
, визначені таблицями Келі:
| + | ||
|
| ||
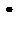
Приклад 4. В полі Галуа 
, яке ізоморфне скінченному полю 
лишків цілих чисел за модулем 7, типові арифметичні операції виглядають так:
,
,
,
.
Характеристика поля
Скінченні поля 
: 
, 
, 
, …, посіли серед скінченних полів місце, яке можна зіставити з місцем, яке відведене полю раціональних чисел 
.
Означення. Поле, яке не має ніякого власного підполя, називається простим.
Теорема. Кожне поле 
містить одне і тільки одне просте поле 
, яке ізоморфне або полю , або полю 
для деякого простого 
.
Доведення. Припустимо, що поле містить два різних простих підполя 
. Тоді за теоремою про переріз підполів 
буде полем (очевидно, непорожнім, оскільки 0 і 1 містяться як в 
, так і в 
), відмінним від і . А це неможливо зважаючи на їх простоту. Отже, просте підполе 
єдине. □
Означення .Кажуть, що поле має характеристику нуль, якщо його просте підполе ізоморфне полю . Кажуть, що поле простої (або скінченної) характеристики , якщо його просте підполе ізоморфне полю . Відповідно пишуть 
або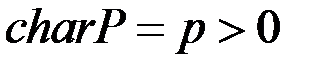 
.
В полі характеристики нуль всі елементи, кратні одиниці поля, нерівні між собою, тобто 
при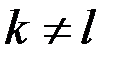 
. В полі скінченної характеристики існують такі цілі числа 
, 
, що 
(або 
). Інакше: якщо одиниця поля є елементом нескінченного порядку в адитивній групі поля, то це поле має характеристику нуль, а якщо одиниця поля – елемент скінченного порядку – характеристика в дорівнює порядку одиниці поля в адитивній групі поля.
Так, числові поля раціональних, дійсних та комплексних чисел мають характеристику нуль, а будь-яке кільце класів лишків цілих чисел за простим модулем – це поле характеристики .
Приклад 5. Поле Галуа має 
, тому що рівність 
у цьому полі виконується при найменшому додатному значенні 
(тобто 
).
Теорема 1 . В полі скінченної характеристики , для будь-якого елемента 
справджується рівність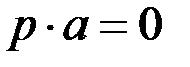 
. В полі характеристики нуль для цілого числа 
з 
випливає 
.
Доведення. Згідно з означенням характеристики поля, в першому випадку 
. А в другому випадку, якби було справедливим твердження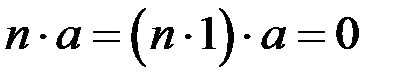 
, то це означало б, що при справджується рівність 
. Через нульову характеристику поля звідси виходить 
, що суперечить умові теореми. □
Теорема 2. Якщо 
– підполе поля 
, то 
.
Справедливість теореми випливає з того, що одиниця поля є одиницею свого підполя.
Теорема 3. Якщо 
, то – просте число.
Наслідок. Характеристика скінченного поля – просте число.
Теорема 4. Будь-яке скінченне поле характеристики містить просте підполе з елементів і є скінченним розширенням цього підполя.
Теорема 5. Нехай – скінченне поле характеристики Тоді для довільних елементів 
, 
цього поля і для довільного 
справджуються рівності
;
(
).
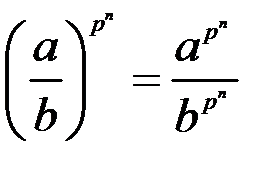